《巧解二次函数面积类问题》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

巧解二次函数面积类问题

范文

吕建虎

【摘要】各地的中考数学压轴题中二次函数都是永恒的话题，它有时甚至是这个试卷难度的风向标，如何提高学生解决二次函数面积类问题的能力，是每一名数学教师必须面对的课题.中考题是命题专家精心设计的作品，而这类问题中也隐含了一些一般性结论，本文将围绕二次函数面积类问题，结合笔者日常教学心得体会，论述如何巧解二次函数面积类问题.

【关键词】二次函数;面积;水平宽;铅直高

初中数学中考压轴题有一种常考的类型，二次函数最大面积问题.常用的方法有割补法、铅垂高法等.学生面对此类问题往往不能顺利地解决，究其原因在于割补法过程烦琐、计算量大、容易出错.本文主要介绍一种巧解二次函数面积类问题的方法，即三角形面积等于水平宽与铅垂高乘积的一半.该方法是铅垂高法的推广，只要顺利表示水平宽与铅直高，就可以巧妙地将面积最大问题转化为二次函数的最大值问题.

一、方法介绍

结论：S△=1 2水平宽·铅直高.

如图1所示，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度AD叫△ABC的“铅垂高（h）”.我们可得出一种计算三角形面积的新方法：S△ABC=1 2ah，即三角形面积等于水平宽与铅垂高乘积的一半[1].

证明如图2所示，通过作铅垂高AD，将△ABC分割成△ABD和△ACD，即S△ABC=S△ABD+S△ACD，过点B作BE⊥AD交AD的延长线于点E，过点C作CF⊥AD交AD于点F，

S△ABD=1 2·AD·BE，

S△ACD=1 2·AD·CF，

S△ABC=S△ABD+S△ACD

=1 2·AD·BE+1 2·AD·CF

=1 2·AD·（BE+CF）

=1 2a·h.

注意事项：1.找出B，C的坐标，横坐标大减小，即可求出水平宽;

2.求出直线BC的解析式，A与D的横坐标相同，A与D的纵坐标大减小，即可求出铅垂高;

3.根据公式S△=1 2水平宽·铅垂高，求出面积.

二、例题精讲

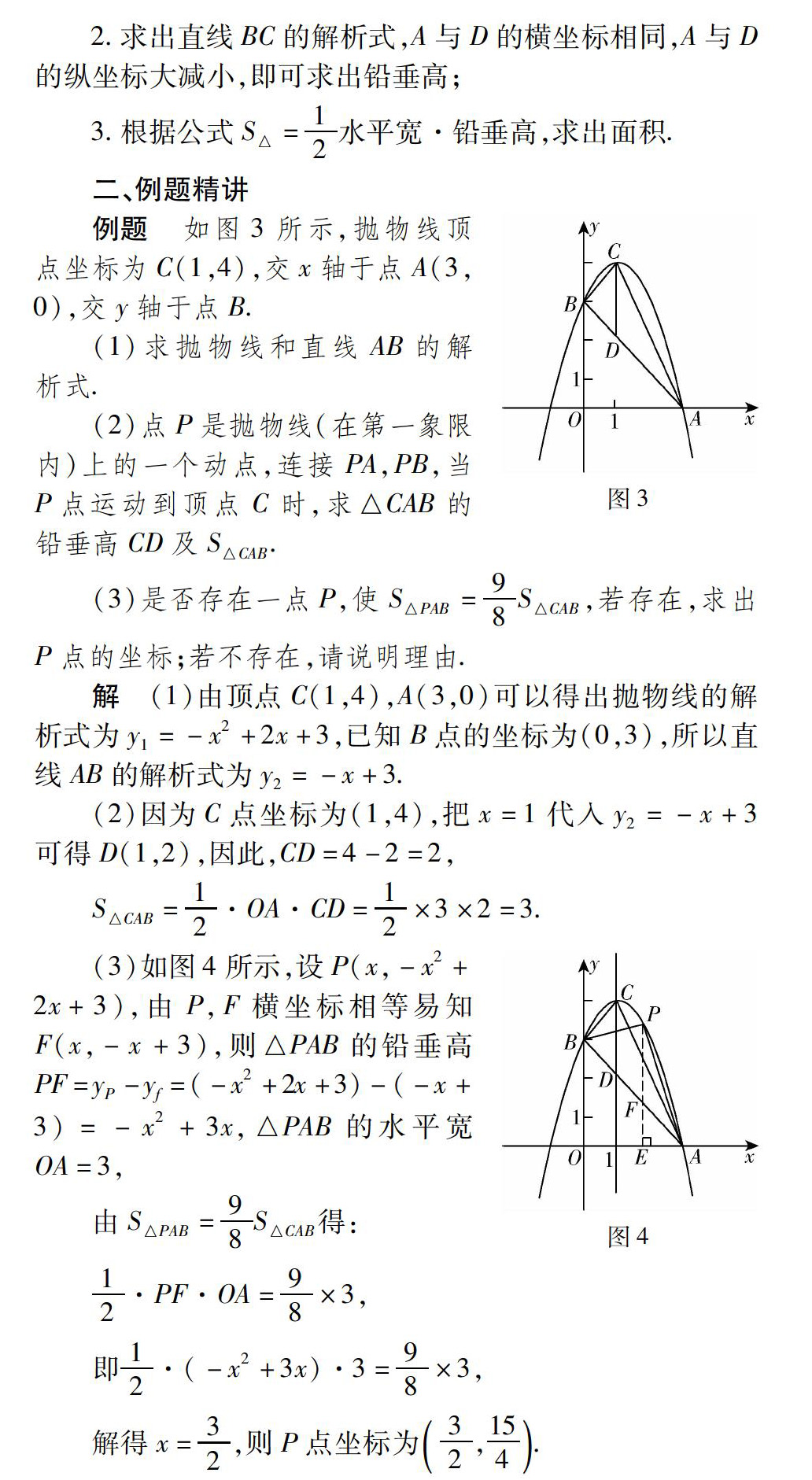
例题如图3所示，抛物线顶点坐标为C（1，4），交x轴于点A（3，0），交y轴于点B.

（1）求抛物线和直线AB的解析式.

（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB.

（3）是否存在一点P，使S△PAB=9 8S△CAB，若存在，求出P点的坐标;若不存在，请说明理由.

解（1）由顶点C（1，4），A（3，0）可以得出抛物线的解析式为y1=-x2+2x+3，已知B点的坐标为（0，3），所以直线AB的解析式为y2=-x+3.

（2）因为C点坐标为（1，4），把x=1代入y2=-x+3可得D（1，2），因此，CD=4-2=2，

S△CAB=1 2·OA·CD=1 2×3×2=3.

（3）如图4所示，设P（x，-x2+2x+3），由P，F横坐标相等易知F（x，-x+3），则△PAB的铅垂高PF=yP-yf=（-x2+2x+3）-（-x+ 3）=-x2+3x，△PAB的水平宽OA=3，

由S△PAB=9 8S△CAB得：

1 2·PF·OA=9 8×3，

即1 2·（-x2+3x）·3=9 8×3，

解得x=3 2，則P点坐标为3 2，15 4.

三、结束语

通过以上例题可以看出，利用这种方法计算三角形的面积的关键是正确表示水平宽和铅垂高，从而巧妙地借助坐标将面积最大问题转化成二次函数最值问题，和割补法相比有很大的优势.希望能开阔学生的视野，找到解题的灵感，使类似问题迎刃而解.如有纰漏，敬请读者指正.

【参考文献】

[1]刘永智.一个三角形的面积计算公式及其应用[J].中学生数学，2014（10）：5-6.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。