网站首页  词典首页

标题	究竟是7s还是8s？
范文	夏艳 追及问题是在指特定的情形下，两个物体在同一直线上运动时所涉及的追及、相遇、相撞问题.我们通常主要研究同向追及问题，其特征是两个运动物体同时不同地（或同地不同时）出发作同向运动，在一定时间之内，后面的追上前面的物体.常常可能涉及何时相遇或最大距离等问题. 其中有一类追及问题涉及到汽车做匀减速运动的情形，同学们在解这类与实际问题相联系的问题时，一定要注意加以分析，尤其是对汽车运动过程的分析，由于这类问题与理想的匀减速运动过程不同，在求解中很容易出现错误. 例题1 如图 在平直的公路上A、B两车都匀速向右运动，A的车速为vA=4m/s，B的车速vB=10m/s，当B车行驶到A车前s=7m时B车突然开始刹车，加速度大小a=2m/s2，从图示位置开始计时，经多少时间A车追上B车. 大部分同学通常是这样做的：设向右为 这种解法表面上看似乎没有问题，其实在解题过程存在一个很隐蔽的错误.那么到底错在哪儿呢？ 同学们都知道，以前我们曾做过一道简单的汽车刹车问题： 某汽车以10m/s的速度在平直的公路上匀速向右行驶，突然发现前方有障碍开始刹车，加速度大小为2m/s2，求6s内该汽车的位移和6s末的速度. 对这个题目，大部分同学的思路如下：设向 在算出6s内汽车位移时绝大多数同学都没觉得没有什么问题，但当算出 6s末的速度是-2m/s时，同学才觉得不大对劲，因为生活中汽车刹车时不可能会再反向运动.所以，以上认为汽车一直以2m/s2的加速度运动的解题过程看似正确，但不符合生活实际.这时大部分人都意识到刹车的时间应该小于6s，正确的解法是先判断停下的时间是5 s，再将Ss代人运算，求得正确结果. 以上汽车匀减速运动问题给我们的启发：当所求时间小于汽车减速停下的时间t0时，可以直接以所求时间代人相关公式运算，当所求时间t大于减速停下的时间t0时应以t0代入公式运算. 此时我们再回过头来看例1的追及问题.因为B车匀减速运动并且是刹车，要先判断B是在被A追上之前已经停止，还是被A追上之后才停止的问题.所以针对这个问题，我们应该首先判断B停下来的时间，然追上，则要先计算在B停下来时A距B的距离，再计算追上的时间. 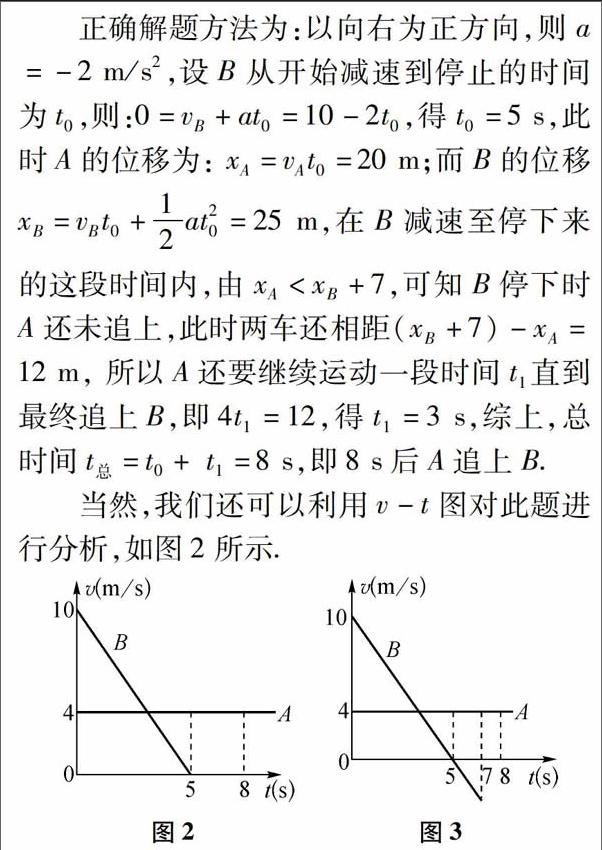当然，我们还可以利用v-t图对此题进行分析，如图2所示. 汽车5s停下时，两车位移分别为对应的矩形面积和三角形面积，很显然B比4的位移大，且此前B已经在A前7m，故此后A要继续匀速，而B停止运动.最后可求得追上的总时间为8s. 通过以上题目我们知道如果被追及物体是刹车的汽车，则要先判断是在被追物体停下来之前还是之后追上，再根据具体情况进行运算. 但是甲同学的做法也有一定的合理性，当追及问题不是汽车做匀减速的，而是变为在外力作用下做匀减速的物体时，可能就是正确的. 例2 如图4.在同一光滑水平面上，A、B两物体均向右做匀速直线运动，A的速度为vA=4m/s，B的速度为vB=10m/s，当A在4前方7m时B突然受水平向左的恒力的作用，做加速度大小为a=2m/s2的匀减速，直到两物体相遇，则从图示位置开始计时，经多少时间A追上B. 此题乍一看与例1一样，但区别在于：此题中B虽然也做匀减速运动，但到速度为零时B并没有停止运动，而是在恒力的作用下继续往左匀加速运动.由例1和例2的v-t图我们也可以发现他们的不同（图3），例1中的B在Ss前的运动和5 s后的运动图象是分段的，所以不能用同一个规律去做，而例2中的B的运动是单一的匀变速直线运动，故可以用同一规律去解题. 由题意可得： 从以上两个例子中我们知道：追及问题，特别是匀速（或匀加速）运动的物体4追做减速运动的物体B，最终结果肯定能追得上，追上时也一定有位移关系 但根据这个关系解题时一定要特别注意：若被追及物体的减速属于汽车刹车问题，则必须先分析匀减速运动的物体B停止运动时A是否追赶上它；若被迫及物体的减速属于可逆向的匀变速，则直接可以运算. 所以，在追及问题中我们要先弄清条件和物理情景，确定模型，理清思路，然后确定位移关系与时间关系，再复杂的问题也能迎刃而解. 练习如图5，在平直的公路上A、B两车都匀速向右运动，A的车速为vA=4m/s，B的车速vB=10 m/s，当B行驶到4前s=7m时B车突然开始刹车，加速度大小aA=2m/s2，与此同时，A车突然加速，加速度大小为 ，从图示位置开始计时，经多少时间A车追上B车.
随便看	浅谈ＣＰＡ学试制度改革对高校注册会计师专业教育的影响 高校财经类专业实践教学研究 财经类专业实训教材开发机制的研究与探索 医院基建工程审计问题浅析 论增值税转型产生的影响 企业固定资产纳税筹划的战略思考 我国股权激励制度存在的问题及对策 新准则下债务重组审计的对策研究 公安系统内部审计实践创新探索 金融审计“免疫系统”的构建 新准则对通用软件架构的企业会计信息系统影响 基于网络的会计信息系统安全分析与策略 浅谈大港油田滩海开发公司成本控制 工业企业物流成本核算存在问题及改进 我国中小企业内部会计控制的相关问题分析 长三角中小外贸企业融资难分析 中小企业融资问题探讨 太钢集团全面预算管理的实践与启示 试论我国产权会计观的确立 基于价值链的现金流管理 论会计职业层次与会计职能的协调 企业特征现金流与投资行为 《事业单位会计准则》设计的若干问题探析 浅谈出纳工作的认识与体会 新准则对会计人员职业素质的要求 courses courseware coursework courseworks course² course¹ court courtcosts court costs courted courteous courteously courteousness courteousnesses courter courtesies courtesy courtesycall courtesy call courtesy of sb/sth courthouse courthouses courtier courtierism courtierly 三过其门而不入 三过家门而不入 三进宫 三连冠 三连霸 三迳 三迹 三逐乡闾 三途 三通 三通一平 三通子 三遍 三遍不忘 三道头 三道杠女友 三道门子 三道防线 三遭为定 三邻四舍 三部曲 三都 三都赋并序 三酉 三酉儿

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。