《陇中半干旱区玉米对光和CO2浓度的响应模型》-农学论文，农业论文-论文范文参考-科学狗论文网

标题

陇中半干旱区玉米对光和CO2浓度的响应模型

范文

丁林凯　阚飞　李玲　岳宁　周琳琳　魏国孝

摘要：为挑选出最适合陇中半干旱区玉米的光响应和CO2响应模型，以甘肃省白银市会宁县种植的玉米为试验材料，使用Li-6400型便携式光合仪测定玉米在不同光合有效辐射和CO2浓度下的光合数据，采用应用较多的非直角双曲线模型、直角双曲线模型、指数模型、M-M模型以及叶子飘建立的光响应模型（以下简称叶子飘模型）与CO2响应模型对光响应数据和CO2响应数据进行拟合。结果表明，无论是光响应还是CO2响应，叶子飘模型均能较好地拟合玉米的光响应和CO2响应数据，可以较准确地描述玉米的光响应和CO2响应曲线，并且对光响应过程中的最大净光合速率（Pn，max）、光补偿点（Ic）、光饱和点（Isat）、暗呼吸速率（Rd）、CO2响应过程中的光合能力（Pn，max）、CO2补偿点（Cic）、CO2饱和点（Cisat）、光呼吸速率（Rp）等光合参数的计算也较可靠。

关键词：光合作用;叶子飘模型;光合有效辐射;CO2浓度;响应曲线

中图分类号： S513.01文献标志码： A

文章编号：1002-1302（2019）08-0086-06

光合作用指绿色植物吸收光能和水分，固定CO2制造有机物，并同时向外界释放氧气的过程[1]。光合作用制造的有机物是植物的生命基础，为生物圈的营养和活动提供能量，是当今能源的主要来源[2]。光是光合作用的主导因子，CO2是光合作用的主要原料[3-4]。研究光和CO2对植物光合作用的影响，需要借助于植物光合作用对光照度和CO2浓度的响应曲线。

光响应曲线是反映植物净光合速率随光合有效辐射变化的曲线，利用光响应曲线可以确定植物的量子效率、光补偿点、光饱和点、最大净光合速率和暗呼吸速率等植物生理特征，使用光响应模型来拟合光合数据，可以反映植物生长过程中的光化学反应过程[5-7]。拟合植物光响应曲线通常用的模型有直角双曲线模型、非直角双曲线模型、指数方程和叶子飘模型等[8-11]。由于植物品种、地域和气候的差异，植物的生理特征会有所不同，适合的模型也不一样。王秀伟等使用7个光响应模型对白桦和兴安落叶松的光合数据进行拟合比较[12];王照兰等使用指数模型拟合扁蓿豆的光响应曲线，对4个不同生态型扁蓿豆的光合特性进行了比较研究[13];陆佩玲等在对冬小麦光合作用的光响应曲线进行拟合时，发现非直角双曲线模型的拟合结果较为准确[14]。

从理论上讲，玉米属于C4植物，而大气中CO2含量的增加对C4植物光合作用没有直接影响，但是某些C4植物对CO2浓度的变化呈现出阳性反应[15-16]。研究表明，在水分亏缺的条件下可以通过提高CO2的含量来增加玉米等C4植物的光合作用强度[17-18]。同研究小麦、水稻、棉花等C3植物的CO2响应的方法相似，研究玉米的CO2响应也借助于CO2响应曲线和模型。CO2响应曲线反映净光合速率随CO2浓度改变而变化的规律，由CO2响应曲线可以确定植物的羧化效率、CO2补偿点与饱和点，以及光合能力和光呼吸速率等光合参数[7]。目前，被普遍应用于植物生理生态等方面研究的CO2响应模型有Farquhar生化模型、直角双曲线模型、Michealis-Menten模型和叶子飘模型等[19-22]。

玉米作为全球第一大粮食作物，研究玉米的光合特性及对环境变化和灾害影响的响应可以为玉米的科学种植与管理提供理论依据，而研究玉米的光合特性需要准确的光响应模型和CO2响应模型。本研究使用不同的模型对玉米的光和数据进行拟合，通过比较模型的拟合结果对各模型进行适用性分析，选出较为适合陇中半干旱区玉米的光响应和CO2响应模型，为后续研究土壤水分条件对玉米光合作用的影响提供模型支持。

1材料與方法

1.1研究区概况

试验地位于兰州大学半干旱区流域地表过程与环境变化野外科学观测站（35°42′N，105°24′E），位于甘肃省白银市会宁县太平镇，海拔1 951 m。会宁县地势由东南向西北倾斜，梁峁起伏、沟壑纵横，属于陇西黄土高原丘陵沟壑区;研究区位于亚欧大陆中部，气候为典型的暖温带半干旱季风气候;研究区位于分水岭的附近，水分较为充足;太阳辐射较强，光照充足，年平均太阳辐射总量为543.92～606.68 kJ/cm2，年日照时数在 2 000～2 800 h，年日照百分率在50%以上;降水较少、蒸发较强导致当地气候干燥，平均年降水量在370 mm左右，多年平均气温为6.4 ℃，年平均蒸发量超过1 800 mm，年无霜期为 136～186 d。试验地为常规种植农田，种植作物为玉米，试验田长为30 m，宽为20 m，玉米植株株距为40 cm，行距为 50 cm，均匀种植，玉米生长期间保持自然生长状态，未进行灌溉、施肥等人为干预活动，测量当年玉米未覆盖地膜。

1.2材料与测定

材料为试验区内常规种植农田中生长良好的玉米植株。测定时间为2017年6月13日08：00—18：00，当天试验地点天气晴朗、无风，叶片温度在28 ℃左右，测量时使用的仪器为美国Li-cor公司生产的Li-6400型便携式光合仪和开放式气路的Li-6400-01液化CO2钢瓶。测定玉米对光照度的响应曲线时，CO2浓度控制在（395.0±1.5） μmol/mol，采用内置红蓝光源控制光合有效辐射强度，设置光照度梯度为 1 800、1 500、1 200、1 000、800、600、400、200、150、100、50、20、0 μmol/（m2·s），测量不同光和有效辐射强度下玉米叶片的净光合速率。测定玉米对CO2浓度的响应曲线时，设定叶片接收到的光合有效辐射强度为1 200 μmol/（m2·s），参比室内CO2浓度梯度为1 800、1 500、1 200、1 000、800、600、400、200、150、100、50、45、0 μmol/mol，测量不同CO2浓度下叶片的净光合作用速率。选取生长良好、叶片完整舒展的玉米进行测量，重复3次，以3次平均值代表实际值。

1.3光合作用对光照度的响应模型

直角双曲线模型

Pn=αIPn，maxαI+Pn，max-Rd。（1）

非直角双曲线模型

Pn=αI+Pn，max-（αI+Pn，max）2-4θαIPn，max2θ-Rd。（2）

指数方程

Pn=Pn，max（1-e-αI/Pn，max）-Rd。（3）

叶子飘模型

Pn=α1-βI1+γII-Rd。（4）

式中：Pn为净光合速率;I为光合有效辐射强度;α为初始量子效率;θ为反映光响应曲线弯曲程度的参数;取值0<θ<1;Pn，max为最大净光合速率;Rd为暗呼吸速率;β与γ为系数;其中β为修正系数。分别求4个公式对光合有效辐射I的一阶导数Pn′，在公式（1）、公式（2）、公式（3）中，对于I取任何大于零的值，恒有Pn′>0，即公式（1）、公式（2）、公式（3）中Pn没有极值，所以在使用公式（1）、公式（2）、公式（3）进行拟合时，不能直接得到植物的饱和光照度Isat，此时需要使用其他方法对饱和光照度进行估算。在利用直角双曲线模型和非直角双曲线模型对光响应曲线进行拟合时，需要对光合有效辐射强度在 200 μmol/（m2·s）以下时的光响应数据使用直线方程进行拟合，得到表观量子效率（AQE），利用最小二乘法估算最大净光合速率Pn，max，然后根据直线方程Pn，max=AQE×Isat-Rd，求解飽和光照度Isat[23]。在利用指数模型进行光响应曲线拟合时，可以假设光合速率为0.9 Pn，max时所对应的光照度为饱和光照度[22]。在利用公式（4）进行计算时，由于该式是一个有极值的函数，将Pn′=0代入公式（4）的一阶导数中即可求得饱和光强Isat，即：

Isat=（β+γ）/β-1γ。（5）

将Isat代入公式（4）中即可得到饱和光照度所对应的最大净光合速率Pn，max：

Pn，max=αβ+γ-βγ2-Rd。（6）

1.4光合作用对CO2浓度的响应模型

直角双曲线模型

Pn=αPn，maxCiαCi+Pn，max-Rp。（7）

Michaelis-Menten模型（后文简称为M-M模型）

Pn=Pn，maxCiCi+K-Rp。（8）

叶子飘模型

Pn=α1-bCi1+cCiCi-Rp。（9）

式中：Ci为胞间CO2浓度;α为在Ci=0时CO2响应曲线的斜率，即初始羧化效率;K为Michaelis-Menten常数，当K=Pn，max/α时，模型（7）和模型（8）为同一个模型，在对光合数据进行拟合时也发现这2个模型的拟合曲线和拟合得到的参数完全一致;Rp为光呼吸速率;b、c为系数。分别求3个公式对CO2浓度Ci的一阶导数Pn′，可知公式（1）、公式（2）均没有极值，公式（3）有极值，所以需要利用其他方法来估算饱和CO2浓度。在利用公式（7）、公式（8）对CO2响应曲线进行拟合时，首先用直线方程拟合CO2浓度在200 μmol/mol以下时的CO2响应数据，得到其斜率CE（羧化效率），然后根据直线方程Pn，max=CE×Cisat-Rp求解饱和CO2浓度Cisat[7]。在使用模型（9）进行拟合时，由于该式是一个有极值的函数，所以将Pn′=0代入公式（9）的一阶导数中即可得到饱和CO2浓度Cisat，即：

Cisat=（b+c）/b-1c。（10）

将Cisat代入公式（9）即可得到饱和CO2浓度对应的玉米光合能力Pn，max：

Pn，max=ab+c-bc-Rp。（11）

1.5数据分析与处理

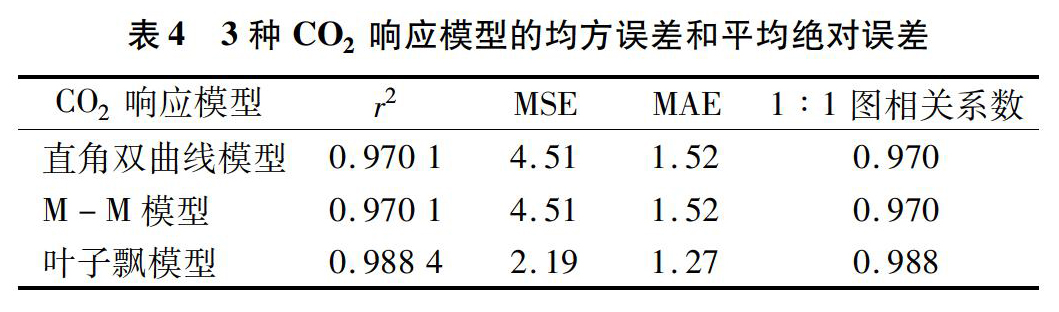
采用Excel 2010进行数据的整理，使用SPSS 22统计软件进行模型的拟合和各项光合参数的估计。使用SigmaPlot绘制玉米叶片光合作用对光照度和CO2浓度的响应曲线。利用均方误差（MSE）和平均绝对误差（MAE）来检验模型的准确性。此外，对实测值和拟合值进行线性回归分析，观察线性回归的相关系数，用以比较模型的拟合度和可靠性。均方误差与平均绝对误差的公式为

MSE=1n∑nt=1yt-y^t2;

MAE=1n∑nt=1|yt-y^t|。

式中：yt代表实测值;y^t代表拟合值;n表示数值个数。MSE和MAE越小，说明拟合值和实测值之间的差距越小，模型越准确[24]。

2结果与分析

2.1光合作用-光照度响应曲线拟合

2.1.1不同模型拟合光响应曲线的比较

从图1可以看出，4种模型拟合的曲线在光照度较低时都呈线性快速增长，当光照度上升达到一定程度时，净光合速率随光照度增长的速率逐渐减小，并且逐渐趋近于饱和，按照光照度可以大致分为线性增长阶段[0～200 μmol/（m2·s）]、过渡阶段[200～1 000 μmol/（m2·s）]、平缓阶段[1 000～2 000 μmol/（m2·s）][25]。在线性增长阶段，曲线斜率较大，净光合速率快速增大，4种光响应模型的拟合点与实测点都比较接近，非直角双曲线较其他3种与实测值的接近程度差一些;在过渡阶段，光合曲线均呈现出由陡变缓的过程，非直角双曲线模型与叶子飘模型的拟合结果比较好，拟合得到的光响应曲线与实测值比较接近;[JP+1]在平缓阶段，直角双曲线模型拟合得到的曲线偏差最大，在光和有效辐射达到 1 500 μmol/（m2·s）以上时，其曲线的斜率仍较大，与实际情况不符，指数方程拟合得到的曲线和直角双曲线模型拟合曲线相比较为接近实测值，但二者趋势相同，在高光合有效辐射强度下，与实际情况偏差较大。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。