网站首页  词典首页

请输入您要查询的论文：

　

标题 初中数学C层教学的实践与感悟
范文 马建


自古以来便有提倡“因材施教”的说法，根据学生的数学基础和思维能力，把学生进行分层走班教学有利于调动每位学生的成长动力，我校从2016年下半年开始尝试进行走班教学.在充分了解、分析学生的数学知识水平和思维能力的情况下，将学生从整体上分成三个层次：A层——数学基础较差，思维能力较弱，学科成绩不好；B层——数学基础一般，思维能力中等，或思维能力较好，但数学基础知识薄弱，成绩一般；C层——数学基础扎实，思维能力较强，学科成绩优秀.下面笔者就本人所教的初二C6班一学期多来印象深刻的几个教学细节作一个简单的梳理，提出几点个人的想法以求同仁的探讨和指引.
1课堂节奏，能“慢”则慢
案例1下面是在学习了“同底数幂的乘法”后，课堂检测时的两道练习题和部分学生解题过程.
感悟作为C层的学生，新课后当堂检测的两道基础题出现如此大面积的错误解法，笔者不禁感到不可思议.学生反映，感觉老师讲课的时候稍微快了些，还没来得及真正体会同底數幂乘法法则的真正含义，把它和合并同类项混淆一块了……回顾本节课的教学过程，笔者认为学生基础非常好，对于他们来说这部分的知识掌握起来应该不是问题，所以在教学过程中节奏不觉间就快了些（PPT内容一闪而过），真正留给学生消化和品悟的时间很少，这说明在课堂教学尤其是在新课学习中，我们的上课节奏不能一味地贪快，一定要做到能慢则慢，快慢结合，否则会出现“欲速则不达”，因材施教也就没有真正得到落实.
2活动探究，以“放”为主
案例2下面是在“平行四边形”章复习课上，笔者呈现了以下一道例题和学生的探究过程.
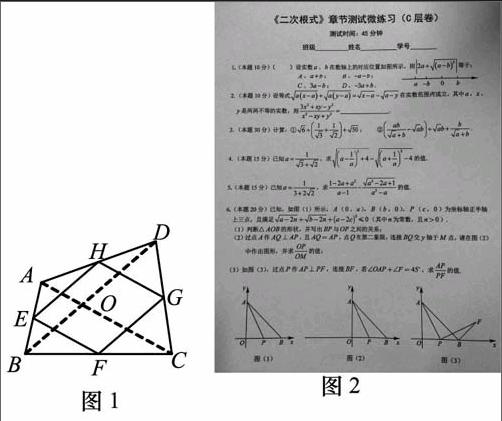
我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.如图1，在四边形ABCD中，E， F， G，H分别是边AB，BC，CD， DA的中点，依次连接各边中点得到中点四边形EFGH.
（1）判断四边形EFGH的形状，并证明你的结论.
（2）如果把四边形ABCD改成平行四边形，那么中点四边形EFGH又是什么形状？
（3）如果把四边形ABCD分别改成矩形和菱形，中点四边形EFGH又是什么形状呢？
题目呈现后，学生经过思考、交流，顺利解决了问题，教师总结后，一个学生提出了一个意料之外的问题.
片段1
师：通过刚才的探究，我们不仅知道了中点四边形肯定是一个平行四边形，而且还弄清楚特殊平行四边形的中点四边形是一个怎样的图形.同学们还有其它的结论吗？
生8：当中点四边形是一个菱形或矩形时，原四边形就是一个矩形或菱形；当中点四边形是正方形时，原四边形就是正方形.
师：哦.生8的结论正好是我们大家得出的结论的逆命题，你们认为他的结论成立吗？
生：……（沉默），好像对的（有同学说）.
师：我们不妨把刚才的探究思路再捋一下，回顾（1），（2）两小题的证明过程，特别是在第（3）小题的研究过程中，无论四边形ABCD在怎样变化，最后都是通过找出谁的关系判断出四边形EFGH的形状的？
生：对角线.
师：对.这就是说对角线AC，BD的关系决定了四边形EFGH的形状，至于四边形ABCD是怎样的四边形重不重要？
生：不重要.
师：你们能说出对角线AC，BD是怎样决定四边形EFGH的形状的吗？
生9：当AC=BD时，四边形EFGH是菱形；当AC⊥BD时，四边形EFGH是矩形；当AC=BD且AC⊥BD时，四边形EFGH是正方形，
师：不错.那么当AC=BD时，四边形ABCD一定是矩形吗？
生：不一定.
师：同样，当AC⊥BD时，四边形ABCD一定是菱形吗？当AC=BD且AC⊥BD时，四边形ABCD一定是正方形吗？
生：不一定.
师：下面请生8同学把你刚才的结论重新完善一下，
生8：当原四边形的对角线相等时，中点四边形是菱形；当原四边形的对角线互相垂直时，中点四边形是矩形；当原四边形的对角线相等且互相垂直时，中点四边形是正方形，
感悟学生能力提升，思维的参与必不可少，生8结论的出现，打乱了教师原有的教学计划.是悬崖勒马，还是纵马前行？若选择悬崖勒马：课后和学生继续探究一下该结论的正确性，那么学生对中点四边形和原四边形之间关系的认识还仅仅停留在一个“面”字上，对C层学生而言在今后的能力发展上可能会是“失之毫厘，缪之千里”；如果选择纵马前行：教学进度要被耽误，教学任务得不到及时的完成.瞬间的权衡后，笔者还是选择了后者，让片段1呈现出来.尽管课堂上浪费了点时间，但学生的参与热情很高，通过正反两向的梳理，从“质”上认清楚是由谁决定了中点四边形的形状.由此可见，教学是否有效，学生能力能否得到提升，并不是指教师有没有及时完成教学任务，而是指教师有没有真正让学生放开手脚融入课堂中来，有所动、有所思、有所获.对于C层的数学课堂，当生成与预设发生偏差时，要根据学生暴露的问题及时调整教学策略和程序，做到“大胆的放，小心的收”，只有“放得开”，才能“收得拢”，有时就是“信马由缰”也不为过.
3检测反馈，太“深”不宜
案例3图2是在复习完“二次根式”后，备课组针对C层班级设计的一份微练习测试卷.测试结果使我们大跌眼镜，全校均分不到40分.经与学生交流、分析，绝大部分学生反映：试卷太难，时间来不及，答题时不知所措，完全乱了套，组内反思：的确挖得深了些，且缺少梯度.
感悟C层学生在数学上不都是非常拔尖的学生，只能说他们这一层次的数学基础较好，对于这一点任课教师要有清醒的认识，同样，分层教学的目的不是让所有学生的数学成绩都达到非常高的水平，而是让所有的学生要在原有的基础上尽可能得到较大的发展和提升，无论是新课中的知识传授，还是复习课后的检测练习，应根据学生的实际学习状况和认知水平，准确把握好深浅程度，做到由浅入深、深浅结合、深入浅出，如果命题时盲目地追求难度和高度，没有注意适度的拓展和延伸，只深不浅，深藏不露，那么对于学生的打击也是不言而喻的.这就提醒着我们，备课组在集体备课时一定要下足工夫，了解学生了解学情，做到适度挖掘，和B层A层学生的要求有一定的距离和区别即可.只知道严格要求，却忽视了让他们量力而行，长此以往，将会事倍功半、功亏一篑，学生学习数学的自信心不断降低，收获越来越小，最终的结果是与我们的期望背道而驰：学生转向B层，走班走向失败.
结束语其实走班教学后所带来的问题远不止以上三点，不但更多而且细碎，如：教材与学材的整合、作业管理和个别辅导、学习纪律和作息方式的要求、师生关系的重新定位……，这些都有待于我们在具体的教学实践中作进一步的关注和研究.苏格拉底曾说：教育是点燃，不是灌输；朱熹也说：指引者，师之功也，其实教育的任务就是激发和促进学生内在潜力的发挥，使其按自身规律获得自然的和自由的发展.数学C层的学生，无疑代表着这一学科中的学习精英，但如果不注意因势利导，科学规范地开展教学工作，那么最终就有可能造成天马行空式的教育失败.在分层走班这种教学组织形式下，只有充分调动学生学习的积极性、主动性，真正做到“主体解放”，从根本上解决“教”与“学”的矛盾，才能使因材施教得到圆满的落实.
参考文献
[1]段作章，正确认识学生是处理好教学关系l的基础[J].江苏教育，2013（05）：16-17
[2]冯复，初中数学教学策略[M].北京：北京师范大学出版社， 2010
[3]庞彦福，初中数学有效教学[M].北京：北京师范大学出版社， 2015
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 13:04:27