《践行学生核心素养培养的初中数学教学策略探析》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

践行学生核心素养培养的初中数学教学策略探析

范文

张彩华

【摘要】数学核心素养是个体素养中最具竞争力的一个品质，数学核心素养培养好坏直接影响着学生未来的发展.因此，从课程标准出发，以核心素养培养为主题，学生为主体，教师引导学生深度学习，将新课程的理念融入数学教学中，让学生在实践中生成数学核心素养.

【关键词】核心素养;初中数学;教学策略

【基金项目】福建省中青年教师教育科研项目（基础教育研究专项）项目编号：JZ190229（福建教育学院资助）

一、创设情境，激发学生积极学习意识

所有数学知识的学习都力求从学生的实际出发，以他们熟悉或感兴趣的问题情景引入学习主题，才能提高学生学习的积极性.而初中生的形象思维高于抽象思维，这就决定教师在教学情境创设上要多下功夫，让生活走进数学.例如，笔者在教“立体图形与平面图形”时，让学生在家做好正方体、长方体、圆柱、圆锥模型，第二天把模型带进课堂，并当场将模型剪开，让学生去感性认识这些立体图形的平面展开图，加强学生对平面图形与立体图形之间联系的认识.同时，在学生感性认识基础上，笔者又创设一个问题情境：“要将一个正方体沿棱展开成一个平面图形，你需要剪几条棱？为什么？”这个问题能够激发学生的思维，增强学生的理性认识，培养了学生直观想象、逻辑推理的核心素养.又如，在教学“变量与函数”时引入一段视频，视频展现的是生活中引入具体变化的生活问题，让学生感受变量，再研究变量之间的关系，最后再引入要学的函数概念，学生学的自然，较易掌握抽象性强的函数概念.再如，在教学活动课“平面镶嵌”的过程中，笔者创设一个故事情境引入课题学习：“一位有钱人，他买了一幢别墅并打算一层全用正五边形瓷砖铺地板，但瓷砖店老板告诉他，你根本就买不到正五边形的瓷砖，有钱人气极了，我金砖、银砖都买得到，何况是正五边形的瓷砖呢！同学们，你们说他买得到吗？”通过这个故事，引起学生极大的学习兴趣，课上学生听得都非常认真，接着让学生拿出准备好的正五边形纸片亲自去拼，感性认识到故事的结论，并以小组讨论的形式理性思考故事结论的原因.上面的三个课例，把教学内容生活化、直观化，让学生有亲切感，也更易让学生接受，在学习中学生自然地生成“直观想象、数学抽象、逻辑推理、数学建模”等核心素养.其实，生活中到处有数学，到处有数学思想，生活本身就是一个巨大的数学课堂，教师如果能从某些生活现象中挖掘出数学因素，恰当创设情境并充分利用，就能使学生轻松地接受数学知识，让他们体会到数学在生活中的价值.同时，创设合适教学情境，让学生具有积极的意识并产生内驱力，才能使学生真正学好数学.

二、深度思考，培养学生思维创造意识

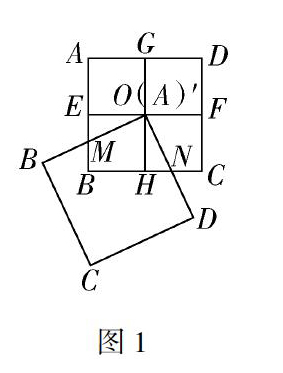
传统的教学，过多强调知识技能，忽视了数学思考、问题解决、情感态度.随着新课程改革的深入，课程目标更加合理和全面，教师选择有思考价值的数学活动，通过问题变式用问题串的形式，以“点”带“面”激发学生的思维，让学生深度思考，更能发展学生思维创造意识，进而培养学生的数学核心素养.笔者常用教材中的“探究活动”栏目里的数学问题进行新课程目标教学.如：两个边长一样的正方形如图1放置，其中一个正方形被两条对称轴EF，GH分成四个同样的小正方形，另一正方形的顶点绕着对称轴的交点O任意旋转，旋转的过程中两正方形重叠部分的面积总等于一个正方形面积的四分之一.想一想，这是为什么？它蕴含着怎样“变中有不变”的观点？开始时，笔者让学生观看几何画板做的动画课件，让学生感性认知结论，接着让学生进行小组合作探究“两个正方形重叠部分面积=一个正方形面积的1/4”活动，并启发诱导证明过程.证明完又出示两个问题，问题一：如果改变旋转正方形的边长，其他条件都不变，那么“两个正方形重叠面积=1/4正方形面积”的结论还成立吗？若成立，请证明;若不成立，请说明理由.问题二：若要使“两个正方形重叠面积=1/4正方形面积”结论永远成立，则旋转正方形边长满足什么条件？这样通过相关知识的变式提问，拓展了学生知识面，激发了学生的学习兴趣和探究热情.同时，课后通过变式作业训练巩固本课的“变中有不变”数学思想的学习，又提高了学生数学思维及直观想象、逻辑推理、数学运算等数学素养，并培养了学生的创新意识.

三、思想渗透，彰显数學的教育价值意识

数学思想是数学学科发生、发展的根本，是探索研究数学所依赖的基础，也是数学课程教学的精髓.数学思想是指现实世界的空间形式和数量关系反映到人们的意识之中，经过思维活动而产生的结果，数学思想是对数学事实与理论经过概括后产生的本质认识，也是对数学规律的理性认识.《义务教育数学课程标准（2011版）》中所说的数学基本思想主要是指数学抽象思想、数学推理思想和数学建模思想，以及由这三种基本思想所派生出来的类比思想、数形结合思想、转化思想、函数思想、方程思想、变中有不变思想等.如“分式”“相似”两章教学，笔者就用类比的思想进行教学，让学生在已有分数、全等三角形知识的基础上轻松掌握分式、相似的新知识.同时，在教学的过程中，笔者将理论结合实践，让数学思想在具体问题中体现出来，让学生真实感受问题解决的过程，并在解决问题的过程中领悟数学的思想.例如，如图，有三碗武夷岩茶，现要放进第四碗武夷岩茶，使四碗武夷岩茶组成一个平行四边形，你觉得第四碗武夷岩茶应该摆放在哪里？选择一个位置，作出这个平行四边形（尺规作图，保留作图痕迹，不写作法）.本题就充分体现了数学抽象思想、推理思想和建模思想，培养了学生的应用意识、创新意识.同时，践行立德树人的理念，也培养了学生热爱家乡的情怀.因此，根据新课程的标准，我们作为一线的教师，要全面研究教材内容，深入挖掘教学内容中所体现的数学思想，使学生获得数学的基本思想，深刻地认识到数学思想的教育价值.

四、文化渗透，绽放数学美学价值

“数学是一种文化”这种观点已逐渐被广大学者所接受.在新课程改革不断深入开展的形势下，数学文化在基础教育中的作用受到日益关注.对数学文化本身的认识、把握，以及在数学教学中如何渗透数学文化与新课程改革下教学质量的提高都密切相关.因此，将数学文化引进课堂，是培养学生核心素养的重要手段.为此，根据学校地理环境及学生的特点，笔者将“武夷文化”引入数学课堂并进行教学，这样做不仅可以让学生提高学习的积极性，领悟武夷文化风情，也唤起学生热爱家乡的情怀，同时，培育了学生的武夷文化情结，弘扬了武夷文化之美.在教学“科学记数法”这一课时，笔者在课堂上这样渗透“武夷文化”：首先，映入眼帘的是“缘聚武夷，茶和天下”课题封面，接着介绍武夷山茶文化，再利用课件出示：世界总人口数约为7000000000人，其中爱喝茶的人约有325000000人.问：生活中的大数怎样来表示呢？引入科学记数法课题，这样引入让学生觉得亲切自然，容易接受，又能在武夷文化氛围中感受科学记数法的学习的重要性.其次，在课堂例题练习环节引入三道题：1.国家提倡“低碳减排”，某公司计划在海边建风能发电站，电站年均发电量约为213000000千瓦时.2.班长一鸣家种了100棵茶树，平均一棵茶树上大约有3700朵美丽的茶花，请问：一共有多少朵茶花？ 3.武夷山脉北段东南麓总面积约999.75平方千米.（用科学记数法表示）这样做让学生在武夷文化背景中提取数学知识，并应用数学知识，进而培养学生数学抽象的核心素养能力.最后，展现一首《咏茶》（宋·苏轼）：武夷溪边粟粒芽，前丁后蔡相宠加.争新买宠各出意，今年斗品充贡茶.吾君所乏岂此物，致养口体何陋耶？洛阳相君忠孝家，可怜亦进姚黄花.教师结合品茶，品“人生甘苦，回味无穷”的人生哲理升华了数学教学的真、善、美！以此题结束本课教学.这节渗透“武夷文化”的基础课，充分挖掘与利用武夷文化资源，让学生身体力行去体会秀美的自然风光，去领会家乡的历史文化，在与自然对话，与古迹文物沟通，与名人和诗人交流中，拓宽视野，增长见识，夯实文化底蕴，提高学生学习兴趣，全面提升学生的数学核心素养，绽放数学美学价值.

五、分层设计，学生个性化的引导提高

学生的学习能力和教育背景是有所不同的，所以个性化的教育和引导很关键.将个性化的引导与学生的自主参与相联系，让不同层次水平的学生都能够在教师的引导下，不断地挖掘个人学习潜能，真正地掌握数学学习的核心要求.下面是笔者针对班级不同层次的学生设计的一道数学题，本题探究从特殊—一般—拓展—延伸—推广，结合具体问题和学生的学情，充分体现学生的差异性.例如，我们知道，平行四边形的面积=底×高，除了利用这种方法外，还可以利用如下方法计算菱形的面积.

③【推广应用】定义：顺次连接四边形各边中点所得的四边形叫作中点四边形.现在第②题四边形RFGH的基础上依次得到3个中点四边形，如图5，求最里面的中点四边形的面积.

本题结合具体问题和学生的学情，为不同发展潜力和能力特征的学生提供可选择的问题并加以解决，促进不同层次学生能力的发展.同时，通过变式探究，让学生加深感受，达成问题解决的目标，培养了学生数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析的六大核心素养.而且，让学生在主动探究、解决问题的过程中领悟数学基本思想，积累数学基本的活动经验，增强学生的应用意识、创新意识和美学价值.

六、微课辅助，提高学生自主学习能力

数学教学活动重心应从关注教学生转到关注学生的学.教师应把教学活动的重心放在促进学生学会学习上.如，笔者设计“变中有不变”微课：两个边长一样的正方形，其中一个正方形被两条对称轴EF，GH分成四个相同的小正方形，另一个正方形A′B′C′D′的顶点A′绕着对称轴的交点任意旋转，旋转的过程中两个正方形重叠部分的面积总等于一个正方形面积的14，想一想，这是为什么？它蕴含着怎样“变中有不变”的观点？本微课是数学实践与探究活动，笔者先让学生课后自主探究，独立解决此问题，后让学生利用微课学习，并配有相关的练习题进行练习，增强了练习题的开放性、应用性、探究性、综合性，进而增强学生提出问题、发现问题、分析问题、解决问题的能力.因此，教师平时在课后可精心设计一些微课，让学生进行小专题探究学习，让信息技术与数学学科有效整合，这样，教师教学方式运用的落脚点最终就放到了提高学生的自主学习能力上，使学生学会学习，并自觉地发展数学学科核心素养.

总之，研究学生核心素养培养是落实立德树人根本任务的一项重要举措，也是适应世界教育改革发展的趋势.培养学生的核心素养是数学教学的重要内容，这就要求教师能够结合时代特性进行课堂教学，引入先进的教学理念，通过多样化的教学手段，帮助学生认知数学本质和现实意义，完善学生的能力和素质，助力学生全面健康发展.教师走在教研的路上，坚定、执着、努力践行着学生数学核心素养培养策略的研究，朝着学生数学核心素养终极培养目标奋进，让学生“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”.

【参考文献】

[1]冯宏亮.数学课堂情景的创设[J].华章（教学探索），2007（05）：73.

[2]李英洁.新课标背景下的初高中数学衔接教学研究[D].苏州：苏州大学，2019.

[3]运士伟，任铭，李守英.数学思想方法在曲线积分与曲面积分教学中的应用[J].教育现代化，2020（14）：21-23.

[4]李海东.积极体现课标理念彰顯教科书育人价值：人教版《义务教育教科书：数学（七至九年级）》的主要特色[J].课程·教材·教法，2013（05）：75-79.

[5]黄翠萍.初中方程教学的理论与实践研究[J].成都：四川师范大学，2019.

[6]兰坤亮.落实培养核心素养要求构建数学高效课堂探析[J].成才之路，2020（03）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。