网站首页  词典首页

请输入您要查询的论文：

　

标题 LMS算法在LFMCW雷达信号处理中的应用
范文 毛亚琼+张荣福+肖鹏程



摘 要：LFMCW雷达在自动驾驶技术中起着举足轻重的作用， LFMCW雷达后端的信号处理是实现雷达作用的关键，然而LFMCW雷达的调制泄漏问题严重影响LFMCW雷达后端信号处理，因此必须去除调制泄漏。自适应对消技术是一种典型抗干扰技术，其基本思想是：滤波器的工作参数随输入信号统计特性的变化而自适应调整，使滤波器一直工作在最佳状态，并将得到的滤波信号与输入信号进行对消。LMS算法提供的滤波器权值迭代公式可以使输入信号沿最快的方向稳定地逼近参考信号。因此，可以将LMS算法运用于自适应对消系统，对泄漏信号进行对消处理。将LMS自适应对消系统应用于实验，结果证明LMS自适应对消系统最大可实现50dB左右调制泄漏对消。
关键词：LMS算法；LFMCW雷达；自适应对消；labview
DOIDOI：10.11907/rjdk.171370
中图分类号：TP319
文献标识码：A 文章编号文章编号：1672-7800（2017）008-0164-04
0 引言
自动驾驶技术发展极为迅速。线性调频连续波（LFMCW）雷达是单位周期内发射频率随时间线性变化的连续波雷达，具有硬件易得、成本低廉、较易调制、算法处理难度低等优点，广泛应用于自动驾驶中。然而LFMCW雷达调制泄漏严重影响雷达功能，这些调制泄漏会造成雷达无法检测近距离目标，同时调制泄漏会形成大量虚警。为使LFMCW雷达准确检测目标，必须对调制泄漏进行抑制。目前的方法有：EMD（经验模态分解）算法[1]、曲线拟合抑制频谱法[2]以及LMS自适应对消法[3]。EMD算法是基于信号的局部特征时间尺度，将信号分解为若干个本征模态函数（IMF），再将泄漏对应的低频段减去，用剩余IMF重构信号[1]。该算法可以有效抑制甚至完全去掉泄漏，但目标信号也可能处于泄漏所处的低频段本征模态中。同时各本征模态间界限难以确定，容易将目标信号去掉，造成近距离目标检测不到。这可能是该算法广泛应用于去噪而没有应用于抑制泄漏的原因。调制泄漏信号的幅度谱类似于一条指数函数曲线，曲线拟合对消法[2]正是根据载波信号这个特点，利用最小二乘法原理拟合出一条曲线，再用调制泄漏信号的幅度谱减去拟合曲线，得到去泄漏后的信号幅度谱。该方法不足之处：①缺乏数学证明；②难以拟合出理想曲线。LMS自适应对消算法是在LMS算法基础上的改进，该算法以含有调制泄漏的中频信号作为参考信号，对调制信号进行调整，从而得到与参考信号均方差最小的信号。将参考信号与调整后的调制信号相减，得到去泄漏的中频信号。本文对LMS自适应对消算法进行研究，并对雷达原始中频信号进行LMS自适应处理，去泄漏效果明显。
1 泄漏产生途径分析
LFMCW雷达的发射机和接收机是连在一起的，当雷达工作时会产生泄漏信号，可能通过4种途径进入接收机成为泄漏：①雷达在接收信号的同时也会发射信号，由于隔离度有限，发射信号会耦合到接收信号中；②在PCB板上：LFMCW雷达的天线一般在一块PCB板上，收发天线距离很近，隔离度一般在30dB左右，存在空间耦合；③存在于芯片中： LFMCW雷达采用收发一体化集成芯片系统，调制信号会在芯片内通过芯片衬底或空间耦合到接收信号中；④产生于电路：发射信号在电路中传输时也会耦合到接收信号中。
本文主要分析调制泄漏对中频信号的影响。调制泄漏使得原始中频信号频谱向低频段频谱“倾斜”，存在“尖峰”，如图 1所示。一般调制泄漏幅度大于目标的中频信号，频率低于目标中频信号时，会导致雷达在进行目标检测时无法有效检测到近距离目标[4]。
2 自适应对消
自适应对消系统结构如图 2所示。自适应滤波器对输入信号u（n）进行滤波处理得到Y（n），将得到的Y（n）与d（n）进行比较，得到误差信号e（n），自适应算法根据误差信号e（n）的值调整自适应滤波器权值。自适应滤波器根据新的权值对输入信号u（n）进行滤波，自适应对消系统沿此环路循环，直到u（n）无限逼近d（n）。
图1 自适应对消系统
原始中频信号由中频信号、调制泄漏和噪声组成。不考虑噪声影响，自适应对消系统必须在保证中频信号不变的情况下去掉调制泄漏，理想的方法是构造一个与调制泄漏等幅反相的信号，与采集信号进行相加实现调制泄漏对消，因此如何构造与调制泄漏等幅反相的信号是实现对消的关键。从泄漏信号产生的途径可以发现，调制泄漏信号来自载波信号，但与载波信号的幅度和相位不等，可通过自适应对消系统对调制信号幅度和相位进行调整，构造一个新信号[5]。因此，在自适应对消系统中，调制信号u（n）为输入信号，原始中频信号d（n）为参考信号，d（n）可表示为d（n）=s（n）+u0（n），其中s（n）為中频信号，u0（n）为调制泄漏。
由于本文自适应算法使用的是最小均方差算法（LMS算法），所以，用Y（n）与d（n）的最小均方差来判断Y（n）与d（n）的接近程度。
误差信号e（n）为：
e（n）=s（n）+u0（n）-Y（n）（1）
对式（1）两边求均方差，得：
E[e2（n）]=E[s2（n）]+E{[u0（n）-Y（n）]2}+2E{s（n）[u0（n）-Y（n）]}（2）
由于s（n）与[u0（n）-Y（n）]不相关，2E{s（n）[u0（n）-Y（n）]}=0，则式（2）
E[e2（n）]=E[s2（n）]+E{[u0（n）-Y（n）]2}（3）
又s（n）是参考信号的一部分，在自适应对消系统中不经过任何处理时E[s2（n）]不变，所以要得到最小的E[e2（n）]，即E{[u0（n）-Y（n）]2}最小，干扰信号u0（n）与滤波器输出信号Y（n）最接近，[u0（n）-Y（n）]最小，也可推得e（n）与s（n）的值最接近[6]。
3 LMS算法
LFMCW雷达的接收信号经正交处理后分别与发射信号进行混频，得到的中频信号是复信号，所以在调制泄漏信号进行对消处理时针对的是复信号。
中频信号[7]可以表示为：
s（t）=Acos（2πf0t+θ0）+jAsin（2πf0t+θ0）（4）
其实部和虚部分别表示为：
sI（t）=Acos（2πf0t+θ0）（5）
sQ（t）=Acos（2πf0t+θ0）（6）
则中频信号可以表示为：
s（n）=sI（n）+jsQ（n）（7）
调制泄漏信号可以表示为：
u0（n）=u0I（n）+ju0Q（n）（8）
参考信号可表示为：
d（n）=dI（n）+jdQ（n）=sI（n）+u0I（n）+j（sQ（n）+u0Q（n））（9）
LMS算法中的滤波器权值可表示为：
w（n）=wI（n）+jwQ（n）（10）
输入信号经过正交变换后可表示为：
u（n）=uI（n）+juQ（n）（11）
滤波器输出信号Y（n）为：
Y（n）=wI（n）uI（n）+wQ（n）uQ（n）（12）
其复数形式：
Y（n）=YI（n）+jYQ（n）=w（n）u（n）（13）
设输入信号和权值分别为：
u=[u1，u2，...uN]T（14）
w=[w1，w2，...wN]T（15）
Y=wTu=uTw（16）
e=d-Y（17）
则LMS自适应对消系统原理结构如图 3所示。
由于调制信号与中频信号相关度不高，所以在计算输入信号与参考信号的互相关时，不考虑中频信号与调制的互相关，设输入信号的自相关矩正为R，与泄漏信号的互相关向量为P，载波自相关矩阵为σ2d ，可分别表示为：
R=E{u（n）uH（n）}（18）
P=E{u（n）u*（n）}（19）
σ2d = E{ u0（n）uH0（n）}（20）
均方误差方程式[8]为：
J（w）=E[e2（n）]=σ2d-pHw-wHp+wHRw（21）
对J（w）求w的微分得：
J（w）=-2P+2RW（22）
滤波器的权值不是固定不变的，每次权值与上一次权值存在更迭关系，可以表示为：
w（n+1）=w（n）+Δw（23）
Δw=-12μJ（w）（24）
由最陡下降算法得：
w（n+1）=w（n）+μ[p-Rw（n）]（25）
式（25）为滤波器权系数迭代公式。
LMS算法步骤[8]：
步骤一： 初始化，n=0
权向量：w（0）=0
估计误差： e（0）=d（0）-Y（0）=d（0）
输入向量：u=[u（0），u（-1），...u（-M+1）]T=[u（0），0...0]T
步骤二： 对n=0，1，2，...
权向量的更新： w（n+1）=w（n）+μu（n）e*（n）
期望信号的估计： Y（n+1）=wH（n+1）u（n+1）
估计误差：e（n+1）=d（n+1）-Y（n+1）
步骤三：令n=n+1 ，转到步骤二。
4 LMS自适应对消系统实现
Labview软件含有封装好的信号处理函数，以及关于LMS算法的自适应滤波器工具包，所以本文采用labview实现LMS自适应对消系统。实现LMS自适应对消主要用到AFT Create FIR LMS VI以及AFT FilterSignal and Update Coefficients VI。AFT Create FIR LMS VI根據更迭步长因子μ和滤波器长度M构造LMS自适应滤波器，AFT Filter Signal and Update CoefficientsVI根据前面构造的滤波器对输入信号进行滤波，将得到的信号与参考信号进行对比，从而更新滤波器的权向量，继续对输入信号进行滤波处理。LMS自适应对消系统工作过程中，必须保证系统稳定性。LMS算法稳定性指权向量均值趋近于最优权向量，输入信号与参考信号的均方差趋近于最小值。要实现LMS算法稳定，迭代步长因子μ必须满足0 <μ<2λmax[8]，λmax为输入信号自相关矩阵的最大特征值。Labview提供的AFTEstimate Maximum Step Size for FIR LMS VI函数可以根据输入信号迅速计算出步长因子μ的最大值，使LMS自适应对消系统能以固定步长方式最快达到收敛。
程序框图见图4。
5 实验结果分析
利用图4所示的程序VI进行LMS自适应对消处理。根据LFMCW雷达检测系统实际情况，设置各项参数如下：
载波：对称三角波，发射信号中心频率为24Ghz，调频带宽B为150Mhz，调频周期T为8ms，采样频率fs为128kHz，目标物体与雷达的距离分别为15m、25m、35m、LMS算法步长因子μ为0.17，LMS算法中滤波器阶数M为2000。参考信号的频谱图如图 1所示，经过LMS自适应对消处理后，滤波器输出信号Y（n）的频谱如图 5所示。
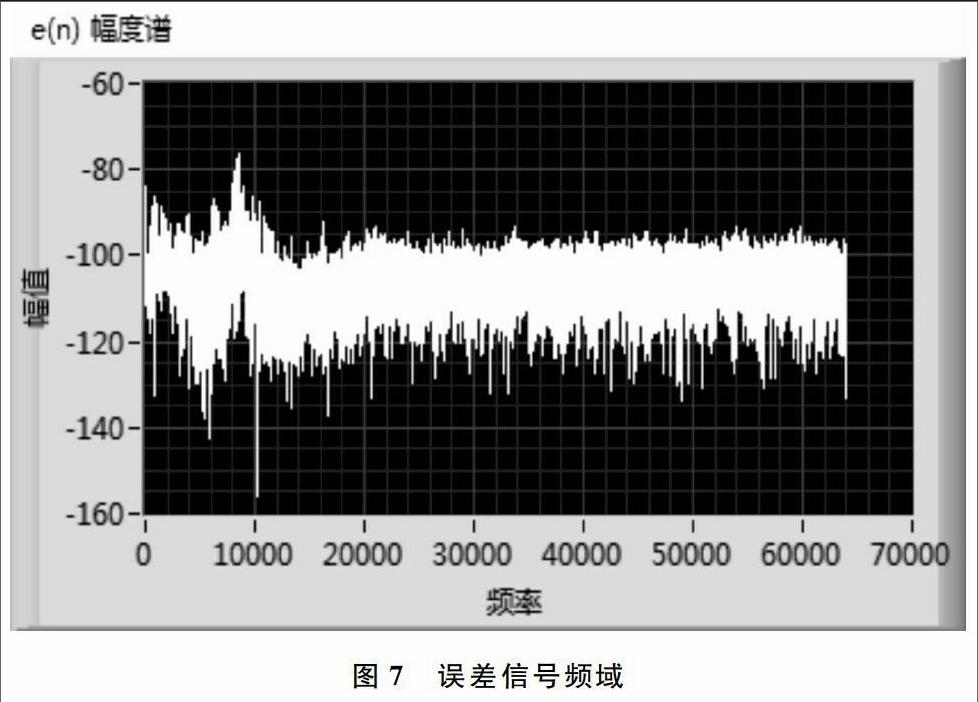
参考信号减去滤波器输出信号Y（n）得到误差信号e（n）即实现对消。图 6为误差信号e（n）的时域图，图 7为误差信号e（n）的频谱图。由图 6可以看到误差信号大约在第600个采样点，即4.68ms后稳定的。对比含调制泄漏的参考信号频谱图 1和经过LMS自适应对消后的误差信号即中频信号频谱图 7，可以看到调制泄漏得到明显抑制：调制泄漏由-55db左右减小到-85db左右，实现了30db的对消，证明LMS自适应对消系统实现了调制泄漏对消。同时发现目标信号的幅度有所减小，分别减小了14db、9db、3db。观察目标信号幅度减小情况发现，目标信号幅度减小不是相同值，而是频率减小越多目标信号幅度减小就越多，即整个LMS自适应对消系统的作用效果相当于高通滤波器。针对这种现象进一步推测，处于近距离的目标在对消过程中是否会由于幅度减小过大而难以检测。为了验证这种推测，分别对1m、2m、3m、4m、5m、10m、15m、20m、25m、30m的目标信号进行LMS自适应对消处理。图8显示1m～5m目标功率的减小情况及相应泄漏减小值。从图中可以看出目标功率的减小值分别为33.25dB、31.6dB、27.86dB、25.71dB、24.14dB时，目标功率的减小值确实随频率的减小而增大的，泄漏功率减小值分别为45dB、44.4dB、50dB、46.57dB、47.1428dB，泄漏功率减小值明显大于目标信号功率的减小值，因此近距离目标信号不会因对消而无法检测。图9显示目标功率减小值分别为33.25dB、24.14dB、16.1955dB、12.96278dB、10.0559dB，说明目标功率减小值随频率的增大而减小。由于泄漏只是对较近距离目标有影响，因此不需要考虑更远目标功率衰减情况。
6 结语
本文对LFMCW中频信号调制泄漏来源及危害进行了分析，并对自适应对消系统和基本的LMS算法进行了研究，在此基础上提出了基于LMS算法的自适应对消系统。实验证明，该自适应对消系统对LFMCW雷达原始中频信号进行处理，可以实现30db左右的对消比，有效抑制了调制泄漏。但是将LMS自适应对消系统运用于LFMCW雷达后端进行调制泄漏对消也存在缺点：系统会在一定程度上削弱目标信号功率，且目标信号功率减小值随频率的增大而减小。但总的来说，LMS自适应对消系统可以有效抑制调制泄漏。
参考文献：
[1] 王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨：哈尔滨工程大学，2010.
[2] 谈锬 .24GHzLFMCW防撞雷达信号处理系统的功能验证及算法研究[D].上海：复旦大学，2016.
[3] 宋妍，王洪，汪学刚，等.基于LMS算法的FOD雷达射频泄漏对消技术[J].太赫兹科学与电子信息学报，2016，2（1）：34-39.
[4] MARK A，RICHARDS.雷达信号处理基础[M].邢孟道，王彤，李真芳，译.北京：电子工业出版社，2008.
[5] 郦舟剑，王东进.毫米连续波雷达载波泄漏对消—理论分析与系统仿真[J].现代雷达，1998（2）：1-2.
[6] 龙戈农，童宁宁，李洪兵，等.改进的LMS算法及其在雷达干扰对消系统中的应用[J].空军工程大学学报：自然科学版，2010，11（5）：127-130.
[7] 黄居敏.连续波雷达自适应载波对消系统设计及应用研究[D].长沙：国防科技大学，2011.
[8] 何子述，夏威.现代数字信号处理及其应用[M].北京：清华大学出版社，2009（6）：134-157.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 23:05:09