《基于观点邻域状态变化的复杂网络传播与干扰模型》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于观点邻域状态变化的复杂网络传播与干扰模型

范文

艾均矫雅楠苏湛

摘要：研究信息或观点在社交网络中的传播对于理解复杂网络理论动力学特征、挖掘传播规律等具有重要理论意义。基于Deffuant模型，設计一种节点状态伴随其自身观点变化而改变的信息传播模型，模型节点具有一个影响其状态的观点值，通过引入状态改变域参数，使节点观点在传播过程中逐渐变化，最终节点状态发生改变，而节点状态则由初始传播者观点邻域决定。在该模型中引入扰动信号源，结合在实际复杂网络结构中的仿真实验结果与相应理论分析模型特征，验证模型正确性与有效性。实验表明，初始观点传播者对最终传播结果具有重要影响作用;作为传播目标的观点，其概念越宽泛，在网络中引发的群体犹豫越大。

关键词：复杂网络;传播动力学;信息传播;干扰模型

DOI：10. 11907/rjdk. 192548 开放科学（资源服务）标识码（OSID）：

中图分类号：TP393文献标识码：A 文章编号：1672-7800（2020）008-0186-06

Abstract： The research of information or opinion spreading in social networks has important theoretical significance for the understanding of the dynamic characteristics of complex networks and the discovery of the regular laws of propagation. Based on the Deffuant model and SI model， this paper designs an information propagation model in which node state changes with its own viewpoint change. With the introduction of the parameters of the state change domain， the viewpoint of the node changes gradually， and finally the state of the node changes. The node state is determined and changed by its viewpoint value and the trust domain of the initial spreader. The disturbance source is introduced to test the opinion spreading with two conflicting viewpoints. The simulation results and corresponding theoretical analysis in some actual complex networks are used to analyze the characteristics of the presented model， and the correctness and effectiveness of the designed model are verified. Experiments show that the centrality of the initial viewpoint spreader in complex networks plays an important role in the final propagation result. If the concept of the spreading opinion is widely accepted， the consequent hesitation of crowds in the network is obviously larger.

Key Words： complex network; propagation dynamics; information spreading; interference model

0 引言

信息传播指信息从初始传播者扩散到其他人群的过程[1]。信息可以是现实生活中的消息[2]、疾病[3-4] 、舆论[5]、计算机病毒[6]等。研究不同环境下信息传播过程有助于掌握信息传播规律[7]、实现消息快速传播，提供免疫策略，为实现舆论控制等提供理论基础。利用复杂网络研究信息传播是近年来相关领域研究热点[8-9]。面对复杂系统分析，复杂网络理论具有独特的分析模型和理解角度，且可基于算法预测网络在演化过程中的变化[10-13]。

传染病模型是信息传播领域较为成熟的模型[14]，该模型认为当感染者疾病传播率大于某一临界值时，感染者会将疾病传播给易感者，这个过程会持续到整个网络感染者均处于某一稳定状态[15]。比较经典的传染病模型有SI模型和SIR模型，它们在发展过程中衍化出多个变种[16]，如类似于 SI 模型的级联模型[17]、考虑到重复感染的 SIS 模型[18]及异构网络中的SIRS模型[19-20]。该类模型传播过程是接触式的，两个节点间发生病毒或谣言的传播，除时间成本外，一般没有传播代价。

消息传播作为现代社交软件发展基础，备受关注，很多学者着力于研究消息传播机理和扩散规律，提出了多个解释模型与预测模型。如Xiong等[21]提出了SCIR 模型，把网络中的人群划分为4类，即易感人群S （susceptible）、接收了消息但不传播的人群C（contacted）、接收消息并继续传播的人群I（infected）和失去传播兴趣的人群R（refractory），该模型认为I和R是消息传播最终稳定的状态;Li等[22]提出改进的SIQRS模型，在模型中加入隔离人群Q（Quarantined Individuals）以研究无标度网络中的传播动力学模型;Xiong等[23]引入潜伏者角色，提出SILR（Susceptible-Infected-Latent-Refractory）模型等。

近年来，观点动力学成为研究热点。为解释和理解观点演变和共识形成过程，众多学者提出了多个模型[24-25]。比较经典的有Deffuant模型[26] ，在該模型中，动态基于二进制交互，其中个体节点意见根据折衷策略成对更新。在全联通网络和无标度网络中，Deffuant模型存在一个普遍的临界置信阈值，在该阈值之上个体最终意见可达成完全一致，在该阈值之下则会存在意见分歧。Shang[27-28]在Deffuant模型中引入了两种不同的置信水平和随机置信水平以考虑异质置信域对观点动力学的影响;Huang等[29]认为当两个个体互相交流时，其观点可能并不总是会跳到平均水平，或以不变的速度发展，因此在Deffuant模型中引入了异质收敛参数。

在这类模型中，传播过程实际上是一对个体节点相互改变对方观点的过程，在消息向外传播过程中，传播者节点向外传播信息是有代价的，其自身观点值在同步其它节点的过程中会依据给定的函数变化，在这些模型中，观点取代了状态，节点类型是影响传播动态的主要因素。因此，这些模型研究的重点大多是网络中观点收敛状态或收敛点，而不是网络中各个节点最终状态。

综合以上讨论可以发现，关于观点动力学，大多数研究集中在置信域和收敛速度。个体之间的影响大多是相互的，但网络结构与观点对模型带来的影响鲜有考虑，也没有用观点值将节点进行状态区分。而现有疾病传播和消息传播等传播模型虽考虑了多次传染或传播才可改变节点状态的情况，但是节点状态改变却没有任何过渡过程，状态之间的转换一次完成，而不是逐渐变化。例如在SI模型中，某种疾病以一定的感染概率在网络中传播，若某个感染者和易感者之间发生感染，则易感者状态会发生变化，变为感染者，继续对其他易感者进行感染，其自身状态不会再发生变化。但在现实世界中，信息传播尤其是观点传播往往不是一蹴而就的，公众对一些信息的态度和观点往往是在朋友或周围人多次“安利”、“种草”或“吐槽”中才逐渐改变态度和观点，节点状态之间的转换应是一个逐步变化的过程。

综合考虑两种模型特点，本文设计结合Deffuant观点同步模型与信息传播过程的思想，假定网络中的个体均保有一种态度，在观点传播过程中，个体节点需被反复同步才能改变自己的态度，并且个体节点不同状态影响该节点对观点的传播能力，而个体节点状态则基于其观点数值的大小进行切换，最后在实际网络上研究模型动力学特征。

1 模型

SI模型是传染模型中最简单的模型，其节点状态分为两种：①感染状态I（Infected），即一个个体感染上某种病毒，则认为其处于感染状态，该个体还会以一定概率感染其邻居个体;②易染状态S（Susceptible），即一个个体在感染之前处于易感染状态，该个体有可能被邻居节点感染。

基于SI模型的节点状态设定可将观点同步模型中的节点状态也分为两类：①传播者（Spreader），具备传播能力，可以一定概率[β]改变邻居节点的观点;②群众（Crowd），不具备传播能力，可能被邻居节点中的传播者改变观点。

在SI模型中，一个个体一旦被感染则永远处于感染状态，但是观点同步过程中除初始传播者外，代理人状态不是固定不变的，故在新提出的SC模型中设置状态改变域[θ]，当节点观点值与初始传播者[S0]的观点差小于状态改变域[θ]时，节点状态发生改变。

考虑一个由[N]个节点组成的复杂网络，其中节点代表人群，节点之间的连边代表两个代理人之间存在关系，每个节点在每个时间步[t]上均有自己的观点值[xit∈[0，1]]。模型中有3个动态参数：置信域[δ]、状态改变域[θ]和传播概率[β]。置信域[δ]取值范围在[0，1]，状态改变域[θ]取值范围在[0，0.5]，传播概率[β]取值范围为[0，1]。初始所有节点观点值均为[C0]，状态为“Crowd”。

然而在现实网络中，人们对同一事件往往有不同甚至完全相反的态度和观点，或者两种信息是互斥的，诸如华为手机好还是小米手机好这两个问题。绝大多数情况下个体观点会对对方观点的传播造成影响。这种想法之间的相关影响可看成一个对传播者观点传播干扰的过程。将该概念进行抽象化，在模型中将这类节点称为“干扰者”（Disturber），与“传播者”（Spreader）、“群众”（Crowd）并列。

另一方面，即便网络中的个体接受了某观点，个体鉴于自身利益或喜好，只会在一定概率下对该观点进行活跃传播，同时必然存在接受某观点却并不声张的个体，将这种接受不传播的被动状态进行抽象化，对应接受来源观点的是 “接受者”（Accepter），对应干扰观点的是“拒绝者”（Rejecter），这两个状态表达节点接受某观点，但并不传播观点。

基于此，本文提出一种新的观点动力学模型——SCADR模型。

在SCADR模型中，本文将节点状态划分为5种：①“传播者”（Spreader）：具备传播能力，若与其邻居节点观点差小于置信域[δ]，则会改变邻居节点观点;②“群众”（Crowd）：节点初始状态，不具备传播能力但可被改变观点;③“接受者”（Accepter）：与初始传播者观点差在状态改变域内，不具备传播能力，不会改变邻居节点观点，自身观点和状态可被改变;④“干扰者”（Disturber）：具备干扰能力，若与其邻居节点观点差小于置信域δ，则可改变邻居节点观点;⑤“拒绝者”（Rejecter）：与初始干扰者观点差在状态改变域内，不具备传播能力，不会改变邻居节点观点，自身观点和状态可被改变。

假定初始传播者和干扰者自身观点与状态均不会被改变，相反，其它节点个体在改变自身状态后与其邻居节点互动中自己的观点会被改变。若一个时间步后节点观点值与初始传播者[S0]或干扰者[D0]的差值小于状态改变域[θ]，则节点状态会发生变化，由“Crowd”变为“Spreader”、“Accepter”或“Disturber”、“Rejecter”，其中变为具有传播能力节点状态的概率为[γ]，如图1所示。

本模型设置5个可调节变量，分别为置信域[δ]、状态改变域[θ]、变为具有传播能力节点状态的概率[γ]、感染概率[β]以及干擾者出现的时间步[tn]，通过这5个变量的变化研究SCADR模型中观点同步的规律。

2 实验结果分析

为研究SC模型观点同步的过程，本文选择具有明显小世界特性的悲惨世界复杂网络作为实验对象，悲惨世界网络中共有77个节点、254条边。根据度中心性选取一个节点作为初始传播者[S0]。此处选取度值为36的11号节点作为初始传播者，并将初始传播者[S0]的观点值设置为0.9，剩下的节点作为初始群众，并将它们的观点值[C0]设置为0.5，将置信域[δ]固定设置为0.5，状态改变域[θ]分别设置为0.05、0.1，将传播概率[β]分别设置为0.5、0.8进行实验，通过实验得出的节点观点同步过程如图2所示。

对比图2（a）、（b）可以发现，随着传播概率[β]的增加，节点观点同步到统一时的时间步逐渐减少。这说明传播者（Spreader）对观点的传播能力越强，群体越容易达到观点统一。对比图2（a）、（c）与图2（b）、（d）可以发现，随着状态改变域[θ]的增加，节点同步速度逐渐增加，同步到统一时的时间步也逐渐减少，因为随着状态改变域[θ]的增加，有资格成为传播者的“门槛”变低，当传播者基数增加，节点观点同步到统一时的时间步也会减少，且随着传播概率[β]与状态改变域[θ]增加。实验表明，某观点的可接受度越大，越容易达成观点一致，因此为加快观点统一可适当降低成为传播者的“门槛”以增加传播者基数。

在SCADR模型实验中，本文依旧选择具有明显小世界特性的悲惨世界复杂网络作为实验对象，将置信域[δ]固定为0.5，在实验开始时根据度中心性算法选择一个节点作为初始传播者，此处依旧选取度值为36的11号节点作为初始传播者[S0]，将其观点值设置为0.9，状态设置为“Spreader”，剩下所有节点初始观点值均设置为0.5，状态设置为“Crowd”，设置干扰者出现时间步为[tn]。在每一个时间步，状态为“Spreader”传播者[i]对其邻居节点进行传播，若传播者和其邻居节点观点差超过置信域[δ]，即[Sij>δ]，则二者观点不改变;如果它们观点差在置信区间内，即[Sij<δ]，则根据式（2）、式（3）改变两者观点值。在第[tn]时间步依旧根据度中心性算法选出一个节点作为初始干扰者[D0]。此处选取度值为22，排在第二的48号节点作为初始干扰者[D0]，将其意见值设置为[0.1]，状态设置为“Disturber”，在后面的每一个时间步，状态为“Disturber”的干扰者对其邻居节点进行干扰。同样，若干扰者和其邻居节点观点差超过置信区间，则它们观点不会改变，如其观点差在置信区间内，则根据式（2）、式（3）改变两者观点值。在每一时间步结束后计算每个节点与初始传播者[S0]和干扰者[D0]之间的观点差[Sij（t）]。如果节点与初始传播者[S0]之间的观点差小于状态改变域[θ]，则节点状态会以[γ]的概率变为传播者，以[1-γ]的概率变为接受者;同样如果节点与初始干扰者[D0]之间的观点差小于状态改变域[θ]，则节点状态会以[γ]的概率变为干扰者，以[1-γ]的概率变为拒绝者。

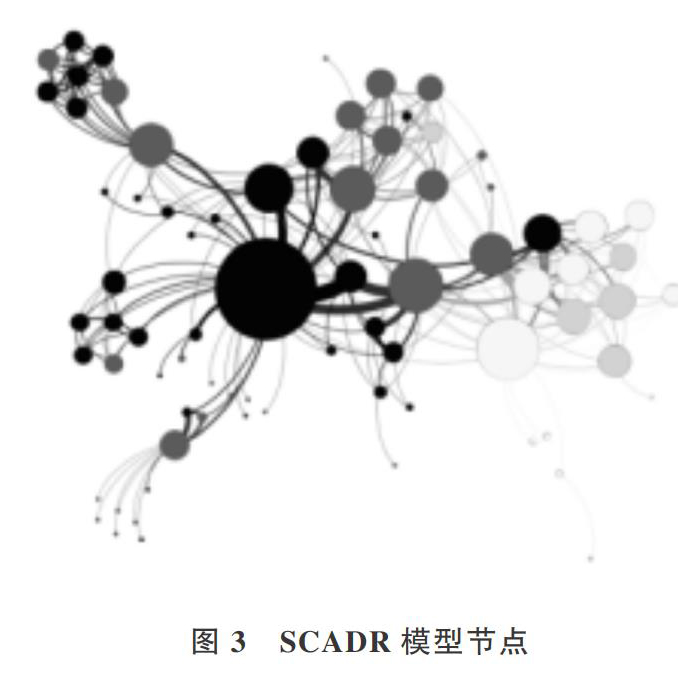
为研究观点同步过程，本文将状态改变域[θ]设置为0.05，将变为具有传播能力节点状态概率[γ]设置为0.5进行实验，将干扰者出现时间点设置为[t2]，依旧根据度中心性算法选择11号节点作为初始传播者和48号节点作为初始干扰者，最终节点状态如图3所示。其中节点大小表示度值大小，连边粗细代表权值，节点状态中黑色表示“Spreader”、深灰色表示“Accepter”、白色表示“Disturber”、浅灰色表示“Rejecter”，观点值演化过程如图3所示。其中，黑色节点代表传播者，深灰色节点代表接受者，白色节点代表干扰者，浅灰色节点代表拒绝者。

图3中，左侧最大的黑色节点是初始选定的传播者，右边最大橙色节点是[t2]时刻选定的干扰者。可以看到初始传播者邻居节点几乎均被“感染”为“传播者”或“接受者”，初始干扰者邻居节点状态也与初始干扰者保持一致，大部分为“干扰者”和“拒绝者”，这说明初始传播者和干扰者的选择对周围社团相同邻居节点的影响很大。

从图4看到大部分节点最终观点值会同步到与初始传播者一致的状态，但在干扰者的干扰作用下，这部分节点同步时间明显比SC模型中相同参数同步时间更长。有少部分节点最终观点值会同步到与初始干扰者一致的状态，这与初始传播者和干扰者节点选择及出现的时间步有一定关系;还可以看出达成观点共识需一定时间，并且同步节点越多，需要的时间就越长。这是因为观点是由初始传播者慢慢向外扩散实现同步的，扩散范围越广，同步节点越多，同时时耗越大。

“Crowd”、“Spreader”、“Accepter”、 “Disturber”和“Rejecter”5种状态节点占比变化如图5所示。由图5可以看出接受某一观点的人数，无论是来自传播者的正面信息，还是来自干扰者的负面信息，其比例在实验末端稳定在一个由网络结构与传播参数决定的值上。但同时，在接受这一观点内部的群体中，活跃的传播者与被动的接受者之间出现周期性的、在观测过程中未见状态循环变化的相互转化过程，网络中的节点同时受到来自对立状态群体与相同状态群体的影响，这种波动现象体现出消息接受群体受到相互冲突消息同时影响下，内心波动情况和作为消息传播受众整体状态的波动情况。

为验证状态改变域[θ]和变为具有传播能力节点状态的概率[γ]对SCADR模型观点传播的影响，本文设计了4组对比实验，如图6所示。图6（a）、（b）中状态改变域[θ=0.05]，变为具有传播能力节点状态的概率[γ]，分别为0.3和0.8;（c）、（d）中[θ=0.1]，变为具有传播能力节点状态的概率[γ]，分别为0.3和0.8。

对比图6（a）、（b）可以发现，网络中所有节点观点值最终均会收敛到与初始传播者[S0]或干扰者[D0]一致的状态，且随着变为具有传播能力节点状态的概率[γ]的增加，节点观点值收敛到一致状态时的时间步逐渐减少。当概率[γ]为0.3时，在50时间步内还不能完成观点值的统一，随着概率[γ]的增加，干扰者和拒绝者最终数量也逐渐增加。由此证明变为具有传播能力节点状态的概率[γ]对观点同步具有一定影响，且概率[γ]越小，节点观点值收敛到一致状态时耗越大，即若某一观点在网络中快速达到统一状态，需提高节点变为具有传播能力状态的概率。

对比图6（a）、（c）和（b）、（d）可以发现，随着状态改变域[θ]的增加，节点观点值收敛到一致状态时的时间步逐渐减少，说明在SCADR模型中，公众对接受度比较广的事件更容易形成观点统一。但是对比图（a）、（c）可发现，当概率[γ]很小，而状态改变域[θ]较大时，干扰者和拒绝者会增加很多，说明对于公众容易改变态度又不愿传播的事情，更容易通过“干扰”控制舆论。

为了进一步研究置信域[δ]对观点传播的影响，在实验中将状态改变域[θ]设置为0.05，变为具有传播能力节点状态的概率[γ]，设置为0.5，干扰者出现的时间步设置为[t2]，置信域[δ]分别设置为0.45和0.6，实验结果如图7所示。

通过图7可发现置信域[δ]越大，节点观点值变化波动越大，但是置信域[δ]对传播者和接受者最终观点达到一致的时间影响不大，对拒绝者和干扰者最终观点达到一致的时间和节点数量影响却比较大。因为干扰者出现在第二时间步，在时间上已落后传播者，此时很多节点观点值已被传播者同步，若置信域[δ]较小，干扰者后续便无力再改变这些节点观点;但若置信域[δ]比较大，即使干扰者出现的时间比较晚，也可改变之前已被同步的节点观点，所以当置信域[δ]较大时，节点观点值波动会较大。

为进一步研究干扰者出现的时间步对观点传播的影响，在实验中将置信域[δ]设置为固定值0.5，状态改变域[θ]设置为0.05，变为具有传播能力节点状态的概率[γ]设置为0.5，将干扰者出现的时间步分别设置为[t3]、[t5]、[t10]和[t15]。

如图8所示，随着干扰者出现时间步的推迟，最终观点值同步在0.1的節点越来越少，但同步速度却越来越快，这是因为干扰者出现的时间步较迟，故只能同步它的某些直接邻居，所以同步速度较快;且若干扰者出现的时间太迟，则不足以改变网络节点观点，但干扰者的出现还是会影响观点同步，使其最终不能达到统一，这是由网络结构决定的。本文实验悲惨世界复杂网络干扰者出现在第15时间步时，最终节点状态如图9所示，黑色表示“Spreader”、深灰色表示“Accepter”、白色表示干扰者“Disturber”，浅灰色代表“Crowd”，可看到未被同步的节点，其邻居节点只有干扰者。

3 结语

本文基于观点同步模型与信息传播模型的思想，设计了SC模型与SCADR观点传播模型，并结合现实社交网络提出更加符合实际情况的传播规则，研究复杂网络中的观点传播规律。通过在具有明显小世界特性的悲惨世界复杂网络与具有明显社团分布的美国政治家博客网络中进行实验，观察SCADR模型观点传播规律。实验发现，在小世界特性的悲惨世界复杂网络中，随着状态改变域及传播概率的增加，节点观点值达到一致的时间大幅缩减，这说明公众对于容易改变态度并乐于传播的事件更容易形成统一观点;通过置信域变化可发现，置信域越大，节点观点值变化波动越大，这也反映了人们对于接受度比较广或概念比较宽泛的观点往往会犹豫不决。通过在美国政治家博客网络中的实验发现，初始传播者和干扰者的选择及网络结构对最终节点观点和状态有决定性影响，并且在SCADR模型中节点特征向量中心性对观点同步的影响比介数中心性更大。在美国政治家博客网络中置信域的变化也反映了对于接受度较广的事情，最终观点值很难达到统一。本文基于观点邻域状态变化且带有干扰源的观点传播模型为复杂网络传播动力学研究提供了新思路。

参考文献：

[1] 汪筱阳，王瑛，朱参世，等. 具有跨邻居传播能力的信息辐射模型研究[J]. 物理学报，2017， 66（3）： 038901.

[2] VALERIO A，MARCO C，MASSIMILIANO L G， et al. Ego network structure in online social networks and its impact on information diffusion[J]. ?Computer Communications， 2016（57）：26-41.

[3] FU R，ALEXANDER G，MARGARET L B. Modeling a dynamic bi-layer contact network of injection drug users and the spread of blood-borne infections[J]. Mathematical Biosciences，2016（273）： 102.

[4] KANG H Y， FU X C. Epidemic spreading and global stability of an SIS model with an infective vector on complex networks[J]. ?Communications in.Nonlinear Science and Numerical Simulation，2016，5（4）：27-30.

[5] HE X S， ZHOU M Y，et al. Predicting online ratings based on the opinion spreading process[J]. ?Physica A， 2015（436）： 658-664.

[6] YANG L X， YANG X F. The spread of computer viruses over a reduced scale-free network[J]. ?Physica A， 2014（396）：173-184.

[7] WANG Q Y， LIN Z， JIN Y H， et al. ESIS： emotion-based spreader-ignorant-stifler model for information diffusion[J]. ?Knowledge-Based Systems，2015（81）： 46.

[8] üMIT A. Effective field theory in larger clusters-Ising model[J]. ?Journal of Magnetism and. Magnetic Materials， 2015（386）： 60-68.

[9] HOU L L，LAO S Y，SMALL M，et al. Enhancing complex network controllability by minimum link direction reversal[J]. Physical Letter A ，2015（379）：13-21.

[10] 李勤敏，郭进利. 基于改进凝聚算法与铁路网的社团划分[J]. ?软件导刊， 2019， 18（1）： 132-135.

[11] 施佳怡，郭进利. 复杂网络视角下上海市加油站布局特征研究——以中石油为例[J]. ?软件导刊， 2019， 18（9）： 146-149.

[12] AI J， SU Z， LI Y， et al. Link prediction based on a spatial distribution model with fuzzy link importance[J]. ?Physica A， 2019 （527）： 121155.

[13] AI J， LIU Y Y， SU Z， et al. Link prediction in recommender systems based on multi-factor network modeling and community detection[J]. ?Europhysics Letters， 2019 （126）：12003-12011.

[14] 盛成成，刘亚平，朱勇. 自媒体复杂网络消息传播模型[J]. 软件导刊， 2019， 18（3）： 157-161.

[15] ROMUALDO P S，CLAUDIO C，PIET V M， et al. Epidemic processes in complex networks[J]. Review of Modern Physics，2015， 87（3）：925-979.

[16] 王賽，刘子龙. 基于复杂网络的SEIA流行病传播模型最优控制研究[J]. 软件导刊， 2018， 17（11）： 194-197.

[17] KEMPE D，JON K，éVA T. Maximizing the spread of influence through a social network authors[C]. ?Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2003：137.

[18] LIU Q M，DENG C S， SUN M C. The analysis of an epidemic model with time delay on scale-free networks[J]. Physica A，2014 （410）：79-84.

[19] LI C H， T C C， Y S Y. Analysis of epidemic spreading of an SIRS model in complex heterogeneous networks[J]. Communications in.Nonlinear Science and Numerical Simulation，2014，19：1042-1054.

[20] CHEN L J， SUN J T. Global stability and optimal control of an SIRS epidemic model on heterogeneous networks[J]. Physica A， 2014 （410）：196-204.

[21] XIONG F， LIU Y， ZHANG Z J，et al. An information diffusion model based on retweeting mechanism for online social media[J]. Phys. Lett. A ， 2012， 376： 2103-2108.

[22] LI T， WANG Y M， GUAN Z H. Spreading dynamics of a SIQRS epidemic model on scale-free networks[J]. ?Communications in.Nonlinear Science and Numerical Simulation， 2014 （19）：686-692.

[23] XIONG F， WANG X M， CHENG J J. Subtle role of latency for information diffusion in online social networks[J]. ?Chinese. Physics. B ， 2016 ， 25（10）：108904.

[24] 熊熙，胡勇. 基于社交网络的观点传播动力学研究[J]. 物理学报，2012，61（15）： 104-110.

[25] 黄飞虎，彭舰，宁黎苗. ?基于信息熵的社交网络观点演化模型[J]. 物理学报，2014，63（16）： 160501-160509.

[26] DEFFUANT G，NEAU D，AMBLARD F，et al. Mixing beliefs among interacting agents[J]. Advances in Complex Systems，2000（3）： 87-98.

[27] SHANG Y. Consensus formation of two-level opinion dynamics[J]. ?Acta Mathethematica Scientia，2014 （34B）：1029-1040.

[28] SHANG Y.An agent based model for opinion dynamics with random confidence threshold[J]. Communications in.Nonlinear Science and . Numerical Simulation， 2014（19）：3766-3777.

[29] HUANG C W， DAI Q L， HAN W C， et al. Effects of heterogeneous convergence rate on consensus in opinion dynamics[J]. ?Physica A ， 2018（499）：266-275.

（责任编辑：江艳）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。