《基于改进粒子群算法的PID参数优化研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于改进粒子群算法的PID参数优化研究

范文

苏攀张伟李强李世港

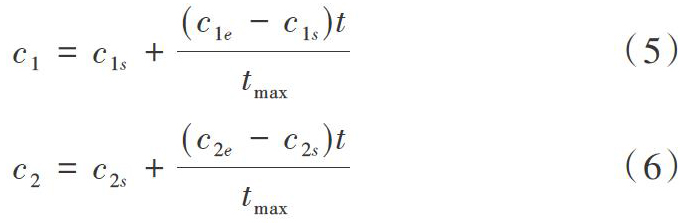
摘要：PID控制是典型的工业控制，其核心内容是PID参数优化。为解决参数优化时不能确保得到最佳性能且耗时问题，通过改进粒子群算法学习因子，研究基于相等随机因子粒子群算法的PID参数优化，将其与标准的粒子群算法及迭代次数线性变化的学习因子进行比较。仿真结果表明，该算法性能指标tr、ts、δ%分别为1.782、3.285、14.07%，两种对比算法的tr、ts、δ%分别为1.804、4.825、24.33%和1.802、4.135、16.56%，改进算法提高了PID参数的稳定性、收敛速度和搜索精度，性能指标更优。

关键词：粒子群算法;参数优化;PID;线性变化;学习因子

DOI：10. 11907/rjdk. 201014

中图分类号：TP301文献标识码：A 文章编号：1672-7800（2020）010-0094-04

Abstract： PID control is a typical industrial control， and its core content is PID parameter optimization. In order to solve the problem that PID parameter optimization cannot ensure the best performance and time consumption， a PID parameter optimization based on equal random factor particle swarm optimization algorithm is proposed by improving the learning factor of particle swarm optimization algorithm. Compared with the standard particle swarm optimization algorithm and the particle swarm optimization algorithm with linear learning factor of iteration times， the simulation results show that the performance indexes tr， ts， δ% are 1.782， 3.285 and 14.07%， respectively， which are better than the tr， ts， δ%： 1.804， 4.825， 24.33% and 1.802， 4.135 and 16.56% of the comparison algorithms. Therefore， the improved algorithm proposed can improve the stability of PID parameter optimization， save time， and obtain better performance indicators. At the same time， the convergence speed and search accuracy are improved， which proves the superiority of this algorithm.

Key Words： particle swarm optimization algorithm; parameter optimization; PID; linear change; learning factor

0 引言

PID控制器诞生至今已有70余年，因其结构简单、稳定性好、鲁棒性强，在工业领域广泛应用，大部分工业控制的反馈回路都具有 PID 结构[1-2]。传统 PID参数优化一般采用 Z-N 法[3]、C-C整定公式法[4]、工业经验等，实践表明这些方法获得的参数并不是最佳参数，改善空间还较大。

随着智能算法的迅猛发展，涌现出许多参数优化方法。孟桂艳[5]将一种改进的果蝇优化算法应用在PID参数整定上以提高果蝇个体寻优能力，改善算法的局部收敛状况;张连强等[6]将融入模拟退火思想的人群搜索算法应用在PID参数优化上。改进算法依据Metropolis准则选择最优解，在一定程度上避免算法过早熟及陷入局部极值，提升算法全局搜索能力;PBOM OLIVEIRA等[7]将引力捜索算法应用到PID参数整定上，解决跟踪目标设定点及干扰控制器问题;Jimenezi等[8]提出将遗传算法用于PID参数优化，在无源光网络管理条件下实验，表明此算法能节省调整时间，提高控制器效率及鲁棒性。

以上方法各有特色，但存在缺陷，如易陷于局部最优点，或使用起来过于复杂等。粒子群优化算法（Particle Swarm Optimization，PSO）是基于群体智能的全局优化算法，由Kennedy等[9]提出。该算法受到飞鸟集群规律啟示，在多维空间内构造“粒子群”进行寻优。算法操作简单，依赖参数少，应用广泛。本文结合PID参数优化，在PSO基础上对学习因子进行改进，并将改进后的算法应用到PID参数整定中。将其与标准PSO和Ratnawecra[10]提出的线形调整学习因子取值比较，以证明改进算法的优越性。

1 PID参数优化

1.1 PID控制器

将比例（P）、积分（I）和微分（D）3种环节并联，可构成比列积分微分控制器，简称PID控制器[11]。设定这3个环节参数可控制被控对象。

其中，[u（t）]为控制器输出，[e（t）]为系统给定与输出量的偏差，[Ti]为积分时间常数，[TD]为微分时间常数，[KP]为比例系数，[KI]为积分系数，[KD]为微分系数。

比例环节反映系统偏差，通过调节能够提高系统灵敏度及系统稳定性;积分环节作用是消除系统稳态误差，改善系统无差度;微分环节反映偏差信号变化规律，依据这些规律进行超前控制调节，改善系统能动性。PID参数优化实际是对3个系数进行优化，如果参数优化不合理，不仅不能达到最佳控制效果，反而适得其反。本文采用改进的PSO对PID进行参数优化，效果较好。

1.2 标准粒子群算法

PSO是通过模拟鸟群觅食行为发展的一种基于群体协作的随机搜索算法，采用速度—位置模型[12]。PSO首先在D维空间中随机初始化一组粒子，这些粒子拥有各自的速度与位置，然后通过迭代方式寻找最优解。每次迭代过程中粒子更新主要依据两个因素：①个体极值点，即粒子自身寻得的最优解[pbest];②全局极值点，即粒子群寻得的最优解[gbest]。粒子群速度—位置更新公式如下：

式（3）中，r1、r2是在（0，1）区间的随机数;c1、c2为学习因子，通常c1=2，c2=2。算法根据式（3）、式（4）循环往复更新粒子的速度、位置，直到达到最大循环次数，或者达到预定的最小适应度阈值，此时的结果即为最优解。

1.3 改进粒子群算法

1.3.1 学习因子研究

根据式（3）可知，粒子速度更新主要由3部分决定[13]：①Vtid，表示粒子的当前速度，换言之是粒子更新前的速度;②c1r1（Ptid-Xtid），表示粒子的自身思考，这部分由学习因子c1、随机变量r1、当前粒子的位置和粒子最优位置构成，由此可见，c1是调节粒子运动到个体极值点的步长;③c2r2? ?（Ptgd-Xtid），这部分表示粒子与整个粒子群之间的信息交流，也就是社会认知，是由c2、r2、当前粒子位置以及整个粒子群的最优位置构成。同理可知，c2是调节粒子向全局极值点运动的步长。

所以在PSO中，学习因子c1 、c2反映了粒子群之间的信息交流;与此同时，c1、c2也决定了粒子自身经验信息及其它粒子经验信息对粒子运动轨迹的影响;c1取值较大，则粒子会在局部过多徘徊; c2值较大会使粒子早熟，陷入局部最优[14]。

Ratnawecra等[10]提出的改进方法将PSO学习因子进行线形调整取值，改进方法如下：

采用随迭代次数线形变化方法，c1取值从2.5～0.5线形递减;c2取值从0.5～2.5线形递增。陈贵敏[15]提出将凹函数方法用于学习因子改进，此方法目的是在早期时加快c1与c2的变化速度，使算法能较快地进入局部搜索，实验结果证明该方法可行。但这些方法缺少多样性，易过早收敛于局部极值，效果不明显。基于此，本文提出基于相等随机学习因子的粒子群算法，试验证明该算法效果较好。

1.3.2 学习因子改进

本文提出基于相等随机的学习因子改进方法。令c1=c2=k，k取0.5、0.7、0.9、1.1、1.3、1.5、1.7、1.9、2.0九组数据，按顺序依次对3个不同的经典函数进行寻优运算，然后对实验结果进行分析。选取相对较佳的寻优结果作为学习因子随机区间，丰富粒子多样性，改善过早熟、陷入局部极值的情况，从而获得较好的收敛性。

采取Rastrigin、Griewank以及Rosenbrock经典测试函数对学习因子进行依次寻优，测试函数描述如表1所示。

九组数据对经典函数进行寻优，迭代次数设为1 000，种群规模为30，寻优次数50次，求平均最优值。通过仿真实验得到表2结果。

将以上数据绘制成散点图进行观察：

对3个经典函数寻优结果及散点图进行分析：①对于Rastrigin函数，当c1=c2=[1.1，2.0]时，寻优结果相对精度较高;②对于Griewank函数，当c1=c2=[0.9，2.0]时，寻优结果相对精度较高;③对于Rosenbrock函数，當c1=c2=[1.3，2.0]时，寻优结果相对精度较高。

基于3个测试函数的实验结果对学习因子进行改进，提出一种相等随机学习因子策略。即c1=c2，且c1、c2随机均匀分布在[1.3，2.0]区间，增加群体多样性。其表达式如下：

将式（7）代入式（3），得到如下表达式：

式（8）与式（4）形成本文改进的PSO速度—位置更新公式。

1.4 参数优化基本思想

本文基于改进的PSO进行PID参数优化，其本质是寻找最优的一组[KP KI KD][16]，换言之就是取合适的系统评价指标作为适应度函数，使粒子群在参数空间里寻找到最优值，使系统达到最优控制性能。基于相等随机学习因子PSO的PID控制结构如图4所示。

对PID控制器性能进行评价时，要求所有指标都达到最佳效果是不可能的，每个参数之间相互影响，难以全部最优，故需要采用能体现综合性能指标最优的系统偏差与时间相联系的性能指标。在众多综合性能指标中，本文选取时间乘绝对偏差积分准则（ITAE）作为改进算法的适应度函数[17-18]：

2 仿真实验

2.1 仿真实验流程

采用MATLAB进行PID参数优化仿真，基于相等随机因子算法流程如下：①初始化粒子群各参数，并确定粒子速度位置;②评价粒子适应值;③将每个粒子适应值与粒子所经历过的最优位置及粒子群所经历的最优位置适应值进行对比更新;④按照式（8）和式（4）进行速度和位置更新;⑤判断是否满足终止条件，若不满足则转向步骤②。

2.2 测试函数仿真

为验证改进算法的优越性，使用标准PSO、文献[10]中改进PSO以及本文改进方法分别对Rastrigin函数进行寻优测试，将结果进行对比。Rastrigin函数表达式如下[19]：

实验将式（3）、式（4）作为标准PSO，式（5）与式（6）代入到式（3）中，然后与式（4）作为文献[10] 改进PSO的学习因子;将式（8）和式（4）作为改进PSO文本。标准PSO学习因子c1=c2=2.0;改进PSO的学习因子c1从2.5～0.5线性递减，c2从0.5～2.5线性递增;本文改进PSO的学习因子c1=c2=[1.3，2.0]，最大迭代次数为1000，精度为0.1，重复仿真50次，得到结果如图5和表3所示。

从图5和表3可知，标准PSO出现早熟，易陷入局部最优，通过改进学习因子提高种群多样性。本文改进的PSO较之于另外两种算法，不论是收敛速度还是跳出局部最优能力都有所提高，寻优结果和精度也有明显改善。

2.3 PID仿真

为证明本文改进算法对PID参数优化的优越性，选取系统控制对象傳递函数表达式如下[20]：

对该系统进行仿真，以ITAE为适应度函数。标准PSO、文献[10]改进PSO以及本文改进PSO在PID参数优化的结果如图6、表4所示。由图表可知，本文改进的算法较之于标准PSO算法和文献[10]改进算法，在PID参数优化上收敛速度和搜索精度均取得较好结果，能够用较少的迭代次数达到最优值，而且本文改进算法在PID参数优化仿真结果的最差值、最优值、方差以及平均值指标上都优于标准的PSO和文献[10]改进的PSO。

图7为改进算法的阶跃响应图。10s时加入一个单位阶跃扰动，可看出本文改进算法有出色的抗干扰能力，表5显示性能指标对比也优于其它两种算法。

3 结语

本文提出一种基于相等随机学习因子粒子群算法，丰富了种群多样性，改善了过早收敛于局部极值状况。PID控制器参数的优化对于系统鲁棒性以及稳定性有十分重要的意义，本文将改进算法应用到PID参数优化上，将其与标准PSO以及文献[10]改进的PSO作对比，仿真结果显示，改进的PSO收敛精度和收敛速度较优，用较少的迭代次数即达到最优值，性能指标更优。

参考文献：

[1] 李献，骆志伟，丁晋臣.? MATLAB/Simulink系统仿真[M].? 北京：清华大学出版社， 2017.

[2] 张霞.? 混沌粒子群优化算法在PID参数整定中的应用[J]. 石油化工自动化，2016， 52（4）： 32-34.

[3] ZIEGLER J G， NICHOLS N B. Optimum settings for automatic controllers[J].? Trans ASME， 1942（64）： 759-768.

[4] COHEN G H， COON G A. Theoretieal consideration of retarded control[J].? Trans ASME， 1953（75）： 827-833.

[5] 孟桂艳. 迭代步进值递减的果蝇优化算法在PID整定中的应用[J].? 青岛大学学报（自然学科版）， 2017， 30（3）： 19-23.

[6] 张连强，王东风. 基于改进人群搜索算法的PID参数优化[J].? 计算机工程与设计， 2016， 13（37）： 3389-3393.

[7] PBDM OLIVEIRA， EJS PIRES. Gravitational search algorithm design of posicast PID control systems[J].? Soft Computing Models in Industrial and Environmental Applications Advances in Intelligent Systems and Computing，2013（188）： 191-199.

[8] JIMENEZ T. An auto-tuning PID control system based on genetic algorithms to provide delay guarantees in passive optical networks[J].? Expert? Systems with Applications An International Journal，2015，42（23）： 9211-9220.

[9] KENNEDY J，EBERHART R C. Particle swarm optimization[C].? IEEE International Conference on Neural Networks， Piscataway，1995（2）： 1942-1948.

[10] RATNAWECRA A， HALAGAMUGE S. Self-orgranizing hierarchical particle swarm optimizer with? time-varying acceleration coefficients[J].? Evolutionary Computation， 2004， 8（3）： 240-255.

[11] 杨平.? PID控制器参数整定方法及应用[M].? 北京：中国电力出版社， 2016.

[12] 杨晓，王国柱.? 基于PID控制理论的改进粒子群优化算法[J].? 控制工程，2019， 26（8）： 1497-1502.

[13] 王博华.? 粒子群算法的改进及其在 PID 参数整定中的应用[D].? 长沙：湖南大学， 2017.

[14] 陈水利.? PSO算法加速因子的非线性策略研究[J].? 长江大学学报（自然科学版）， 2007， 4（4）： 1-4.

[15] 陈贵敏.? 粒子群优化算法的惯性权值递减策略研究[J].? 西安交通大学学报，2006， 40（1）：53-61.

[16] 李晓含.? 基于细菌觅食算法的PID参数整定[D]. 兰州：甘肃农业大学， 2018.

[17] 赵志刚，林玉娇，尹兆远. 基于自适应惯性权重的均值粒子群优化算法[J].? 计算机工程与科学， 2016， 38（3）： 501-506.

[18] 李恒.? 改进的萤火虫算法及其在PID控制器参数整定中的应用[D].? 合肥：安徽大学，2017.

[19] 林玉娇.? 基于改进粒子群的PID参数整定应用研究[D]. 南宁：广西大学，2015.

[20] 史峰. MATLAB智能算法30个案例分析[M].? 北京：北京航空航天大学出版社，2011.

（责任编辑：杜能钢）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。