《基于MATLAB的小波阈值滤波与应用》-工学论文，软件工程论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

基于MATLAB的小波阈值滤波与应用

范文

王赛男++邢冬梅

摘要：小波对分析信号滤波有其独特的优势，本文介绍了小波滤波的原理和常用的小波阈值滤波法，分析了阈值滤波的理论基础和阈值函数数学表达式。最后通过MATLAB实现小波阈值滤波器的设计与仿真，最终利用高低通滤波器来分解和重构有噪声的信号。

关键词：小波阈值滤波；滤波器；分解；重构

中图分类号：TP391.41 文献标识码：A DOI：10.3969/j.issn.1003-6970.2015.10.027

引言

小波滤波与传统滤波相比因小波变换具有时频局部化特性和多分辨的特性，使其在去除噪声方面有独特的优势。对于信号与噪声频谱重叠时，传统的基于傅立叶变换的信号滤波法已经没有办法实现去噪。然而，小波变换可以根据重叠的信号和噪声的小波系数在单层或多层尺度上的不同性质，采用相应的规则，对含有噪声信号的小波系数进行取舍、抽取或切削等非线性处理，达到滤波目的。大量的事实证明，小波在信号去噪处理方面已经取得较好的效果。

l 小波滤波的原理

小波变换除了具有时频局部化、多分辨的重要特性外，还具有去相关特性和选基灵活的特点。因此在去除噪声的同时，还能很好地保留信号的突变部分或图像的边缘部分。

小波滤波的原理过程可以简单的描述为；（1）选择合适的小波并确定变换层数；（2）对实际信号（含噪信号）进行小波分解；（3）通过一定的规则对信号和噪声的小波系数进行非线性处理；（4）用新的小波系数重新构造信号，即得到滤除噪声后的信号。但是在用小波进行滤波时还应注意如下几点：（1）非平滑性。小波滤波是尽可能的去除含噪信号中的所有噪声，而保留所有信号，因此在滤波过程并不考虑频率范围，不能兼顾平滑性（平滑性特指去除高频信息而保留低频信息）；（2）小波滤波是小波变换域对小波系数进行非线性处理。

小波滤波常见的滤波法有：（1）基于信号奇异性的模极大值重构滤波，其思想是根据信号和噪声在小波变换各尺度上的不同传播特性，剔除由噪声产生的模极大值点，保留信号对应的模极大值点，然后利用剩余模极大值点重构小波系数，恢复信号。（2）基于信号尺度间相关性的空域相关滤波，其思想是信号的突变点在不同尺度的同一位置有较大的峰值出现，噪声能量却随着尺度的增大而减小。（3）基于小波变换相关特性的小波域阈值滤波，其思想是通过在不同尺度上选取合适的阂值，并将小于该阈值的小波系数置零，而保留大于阈值的小波系数，从而使信号中的噪声得到有效的抑制，最好进行小波逆变换，得到滤波后的重构信号。鉴于小波阈值滤波法实现具有简单、计算量小、滤波效果好、适用于低信噪比信号处理等优点，本文主要详细介绍小波阈值滤波法。

2 小波阈值滤波的理论基础

2.1 常见的阈值形式

（1）通用阈值（也称为DJ阈值），由Donoho和Johnstone提出的统一阈值（VisuShrink）：

其中σ为噪声标准方差，N为信号的尺寸或长度。这算法是假设在噪声是正态高斯模型，并且是多维独立正态变量联合分布，在维数趋向无穷时的研究得出的结论，即大于该阈值的系数含有噪声信号的概率无限趋于零。该阈值由于与信号的尺寸对数的平方根成正比，所以当N值较大时，阈值将所有小波系数趋向置零，因此小波滤噪器退化为低通滤波器。

（2） SureShrink阈值，在本阈值算法中假设W为一向量，其向量为小波分解系数的平方，并且该小波分解系数按从小到大的顺序排列可以表现为W= [Wl，wz，…，Wn而且Wl《W2《…《Wn，；再假设向量R，其向量可以表达为：其中以R向量中的最小值rmin作为风险值，通过rmin的下标min求出向量的Wmin，可以得到阈值表达式为：

（3）HeurShrink阈值，在通用阈值和SureShrink阈值的基础上，假设S为N个小波系数的平方和，则可以令，可以得到阈值表达式为：

（4） MinimaxShrink阈值（最小极大方差阈值），与前面三种阈值不一样，它是一种固定的阈值，在所选定的阈值中使它们产生最小的极大方差。其表达式如下：

（5）基于零均值正态分布的置信区间阈值，表达式如下：

TH5=3σ～4σ

（5）

这个阈值的思想是根据大量的实验发现：零均值正态分布变量落在[-3σ，3σ]之外的概率非常小，因此绝对值大于30的系数一般都会被认为主要由信号系数构成。

上述几种阈值有其优点，也有其缺点，其中VisuShrink阈值计算量简单，因此在实际中得到了广泛的应用，但是通常计算得到的阈值过大，从而会导致信号中过多的高频信息丢失。SureShrink和HeurShrink阈值，是以估计重建均方误差最小阈值的作为阈值，在该过程要寻找趋向于多个小波系数，阈值的选择存在风险。MinimaxShrink阈值基于最大均方误差最小化，即使置信区间的阈值跟图像（信号）尺寸大小没有关系，但是随着图像尺寸增大，大的噪声系数出现的数目会增多，并且会被保留，因而会导致误差也增大。

2.2 阈值函数

阈值函数也是小波阈值滤波法的基本要素。在小波阈值滤波过程中采取不同的阈值函数，则对系数处理策略和估计方法也会不同。目前常用的两种阈值函数是：软阈值函数和硬阈值函数。其中硬阈值函数的数学表达如下：

在硬阈值函数表达式式中，其中w（j，k）为含噪信号分解后的小波系数，九为选定的阈值，W（j，k）是硬阈值函数处理过的小波系数。硬阈值函数会直接把绝对幅值小于选定为阈值的点取零，而保留绝对幅值大于阈值的点。

软阈值滤波函数的数学表达式为：

软阈值滤波函数不单只抑制幅值较小的小波系数，而且还可以抑制所有的小波系数。

总之，软阈值和硬阈值函数的基本思想都是去除小的小波系数，对大的小波系数进行收缩或保留。软阈值会造成一定的高频信息损失，因而给重构带来不可避免的误差。

3 仿真结果分析

本仿真在MATLAB下，通过滤波函数与dwt函数混合使用，用db4小波单层分解带有随机噪声的信号，并设置高、低通滤波器，从而利用滤波器来分解信号，最后重构信号，并计算误差值。

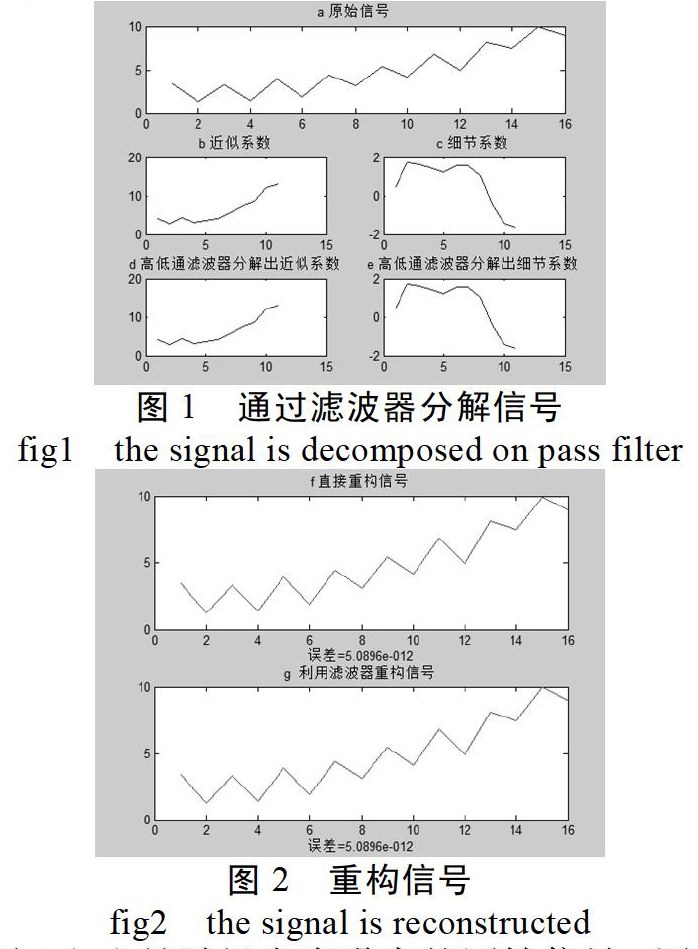
图l（a）是随机含有噪声的原始信号，图l（b）是图l（a）中信号的近似系数，图l（c）是图l（a）中信号的细节系数，图l（d）是通过了高低通滤波器分解得到的近似系数，图1 （e）是通过了高低通滤波器分解得到的细节系数，对比图1（b）与图1（d），图1（c）与图1（e），图中曲线几乎一样，没有的明显变化，该实验结果表明：比较分解出的近似系数和细节系数，用db4小波通过高低通滤波器能有效地单层分解带有随机噪声的信号。

图2 （f）是直接对原始分解的信号进行重构，图1（g）是通过滤波器对分解的含噪信号重构，通过对比图l（a）的原始信号，在曲线上没有太大明显的区别，通过设计的程序函数计算原始信号和重构得到信号的误差，差值为5.0896e-012是可以接受的范围。

4 结论

通过上面的结果分析得到：含噪信号通过设置的高低通滤波器进行小波分解和重构，近似系数和细节系数都没有明显的误差，重构信号与原始信号误差较少。两个基于MATLAB模拟仿真实验结果表明：用db4小波一层分解即使通过高低通滤波器也能有效地分解和重构带有随机噪声的信号。该实验很好的体现了小波阈值滤波的优点：实现简单，计算和编程量小，去噪效果明显。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。