网站首页  词典首页

请输入您要查询的论文：

　

标题 基于GLUE和标准Bayesian方法对TOPMODEL模型的参数不确定性分析
范文 赵盼盼 吕海深　朱永华 欧阳芬



摘要：目前，水文模型不确定性的量化问题在水文研究中受到很大关注，在一些文章中提到了许多不确定性量化的方法，其中，GLUE方法和标准Bayesian方法是两种最常用的方法。主要讨论这两种方法在研究TOPMODEL 模型时计算有效性和不同之处.通过用GLUE和标准Bayesian方法估计TOPMODEL模型参数的不确定性和模拟的不确定性，对这两种方法的结果进行评价，并讨论产生不同的原因，研究的主要结果为：（1）由Bayesian方法得到的参数后验分布比GLUE方法得到的离散型小。（2）给定GLUE中阈值（=0.8）的情况下，由Bayesian方法得到模拟流量的不确定性置信区间与GLUE方法得到的很接近。
关键词：GLUE；Bayesian 方法；TOPMDEL模型；不确定性；敏感参数；拟合；置信区间
中图分类号：P334 文献标志码：A 文章编号：1672-1683（2014）06-0044-05
概念水文模型是水文循环模拟的常用工具。它用于水量平衡分析、延伸和加密径流记录、流量预测、蓄水操作、水量供应和流域管理等。概念性模型的明显特征是一个或者多个的参数需要用物理概念观察集水区响应来校正[1]。当参数校正时，它容易出现多个校正周期从而产生多个优化参数集，并且在单一周期中，优化参数值的不同集合内也可能会产生相同的模型性能，在水文学上把这种现象称为“等度”。另一方面，不同的模型，即使有相似校正结果或者相同的输入和输出数据，也可能会产生不同的预测[2]。因此，在水文模拟中的不确定性问题受到较大关注。
一般来说，产生不确定性的原因有三种：输入数据和校正数据的误差，不完整的模型结构，以及模型参数的不确定性[3]。Xu[4]说明了降雨数据的质量对模拟误差和校正模型参数的影响，Engeland[5]说明了模型结构的不确定性比参数不确定性对概念水量平衡模型的总模拟不确定性影响大。MarshaⅡ[6]说明了模型结构的不确定性需要形成选择，多个模型的输出集中在一起为产生水文总体来描述不确定性，Kavetski[7]和Chowdhury and Sharma[8]说明了通过自主增加噪声的输入数据，然后在噪声和参数误差间形成一个经验关系。
目前，已有许多方法研究参数不确定性和模拟结果的不确定性。例如，由Beven and Binley提出的广义似然不确定性估计（Genralized Likelihood Uncertainty Estimation（GLUE））方法、用Metropolis-Hastings（MH）算法的标准Bayesian方法、MCMC（Markov Chain Monte Carlo）方法等[9-12]。在许多情况下，不容易直接比较GLUE方法和Bayesian方法。原因一，标准的Bayesian方法尝试减少输入、输出、参数和模型结构等误差的影响，并且试图使统计结论不同[13]。GLUE没有对总的不确定性影响因素分离，虽然它不能指出模型中什么元素构成不确定性，但是它更容易运用和理解。原因二，运用标准Bayesian方法过程中，通常在计算不确定性区间时，需要对精确的似然函数假定，或将其转化成一个较一般的未知形式，然而，GLUE方法通常用于计算流量模拟的不确定性区间，具有统计的非正式似然函数。
本文以淮河史灌河流域的黄泥庄集水区为例，拟采用GLUE和Bayesian方法估计概念水文模型TOPMODEL的参数不确定性，并分别对模拟结果进行检验，讨论其差异及原因。
1 区域概况及模型原理
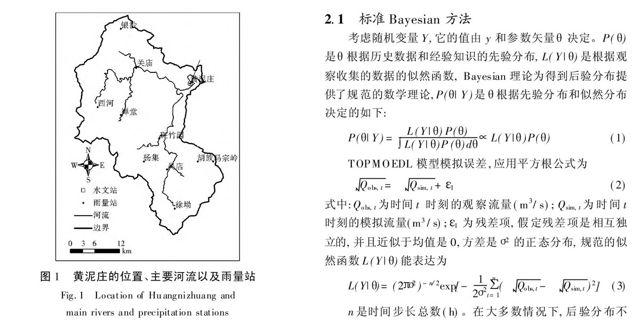
黄泥庄流域位于北纬31°28′，东经115°37′，此区域位于大别山北麓，淮河史灌河流域南部，集水面积为808 km2。地处我国南北气候过渡带，属亚热带季风气候，气候温和，年平均气温为11 ℃～16 ℃。气温变化由北向南、由沿海向内陆递增。区域内地形以山地为主，植被良好，森林覆盖率高达65%，区域的数字地形数据采样GTOPO30数字高程模型，此数据由EROS数据中心研制。该数字高程模型的空间分辨率为30 s（接近1 km），垂直分辨率为1 m。此集水区内有11个雨量站（见图1），获取了1998年逐日降水，平均气温，最高气温，最低气温，平均气压，相对湿度，日照等日值资料
以及1998年5月1日至8月31日的降雨（P）、蒸发（E）、流量（Q）等资料。
1979年Beven和Kirkby[14]基于变动产流面积的概念提出了TOPMODEL（Topography Based Hydrologicl Model），是一个以地形为基础的半分布式流域水文模型。这个模型能够模拟暴雨径流形成的变动源面积，以及能够体现水流过程中地形的影响。TOPMODEL模型是以两个假设为前提的：（1）饱和层的动力学可以由某一面积上的饱和层坡面上某一点排水的连续恒定状态近似表示；（2）饱和层的水力梯度可由根据平面图距离量测的当地地表的地形坡度近似表示。
TOPMODEL的主要特征是以地形空间变化为主要结构，利用地形指数（lnα/tanβ）形式描述水流趋势，基于重力排水作用径流沿坡向运动原理，模拟径流产生的变动面积概念，尤其是模拟地表或地下饱和水源面积的变动。它的主要特征是考虑了流域地形、地貌、土壤等因素对径流形成的影响，并将集总式水文模型计算和参数方面的优点与分布式水文模型物理基础的优点结合在一起。由于TOPMODEL模型的结构简单，参数少，物理概念明确，该模型已在水文领域得到了广泛的应用，并在不断的改进和完善[20]。
地形指数（lnα/tanβ）是一个水文相似性指数，其中α为流经坡面任一点i处单位等高线长度的汇水面积，tanβ为该点处的地表坡度。在本文中地形指数是30 m网格大小的集水数字地形模型，利用Quinn的多流向算法得到。
模型的参数：M为土壤下渗呈指数衰减的深度（m）；SK0为饱和带的平均水力传导（m/h）；LRZ为根部的深度（m）；KS为土壤达到饱和时的导水率（m2/h）；Td为重力排水的时间滞时参数（d）；SRmax为植被根系区的最大蓄水能力（m）；SR0为根带土壤的初始缺水量（m）；RV为地表坡面汇流的有效速度（m/h）；CHV为主河道汇流的有效速度（m/h）。这个模型是以每小时为时间步长，并假设在全流域内有相同的土壤性质。
2 研究方法
2.1 标准Bayesian 方法
考虑随机变量Y，它的值由y和参数矢量θ决定。P（θ）是θ根据历史数据和经验知识的先验分布，L（Y|θ）是根据观察收集的数据的似然函数， Bayesian理论为得到后验分布提供了规范的数学理论，P（θ|Y）是θ根据先验分布和似然分布决定的如下：
式中：Qobs，t为时间t时刻的观察流量（m3/s）；Qsim，t为时间t时刻的模拟流量（m3/s）；ε1为残差项，假定残差项是相互独立的，并且近似于均值是0，方差是σ2的正态分布，规范的似然函数L（Y|θ）能表达为
n是时间步长总数（h）。在大多数情况下，后验分布不是标准形式，尤其在水文模型中。可是为了总结信息，样本可以从后验分布中用MCMC得到。
在Bayesian方法中用MCMC方法估计参数。MCMC从Markov链结构中产生符合后验分布的参数值样本。它从最初的样本值开始，用建议分布产生新的值，然后计算可接受概率，决定是否接受和拒绝新值，然后移除初始的值，样本可能符合后验分布[1，6，15]。
在运用Bayesian方法时出现的一个问题是：建议概率密度函数的选择。建议候选密度的变量影响从当前状态到候选状态以及它可能被接受的概率。如果这个变量太小，迭代过程归纳出的Markov chain 不能很好结合参数空间，后验区域也不能充分采样。如果变量太大，后验分布会经常被拒绝。Chib and Greenberg[16]说明了在链中新一个点的可接受率是45%时将会得到合理高效的链。这个方法的另外一个问题是：对于后验分布这个链的收敛性判断，它可以用点样本粗略的观察判断。如果均值和方差是稳定的，Gelman and Rulun提出了定量的观测、R统计，它使得链间的方差和链内的方差有直接的关系，从而检测收敛性。从参数空间的任意值开始，本文用正态分为作为建议分布产生5个平行链，可接受率在40%～50%。在估计不确定性前，直接观察和R统计计算都是用来检测链的收敛性。
2.2 GLUE方法
GLUE框架是Beven和Binley[16]用于评价预测结果不确定性提出的，GLUE过程是一个MC方法，客观定义了一系列行为模型包含全域的可能模型/参数分布。术语“行为”是用来定义模型，用于判断是“可接受的”，即：不排除[17-18]。GLUE方法中一个很重要的观点是：模型模拟结果的好坏并不是由模型中的某个参数所决定，而是由一组模型参数来决定.在预先设定的参数取值范围内，利用Monte Carlo随机采样方法获取模型的参数值组合，将该参数值代人模型中.选定似然目标函数，计算模型模拟结果与实测值之间的似然函数值，再计算这些函数值的权重，得到各参数组合的似然值。在所有的似然值中，设定一个临界值，这个临界值的选取带有一定的主观性。低于该临界值，表示这些参数组不能表征模型的功能特征；高于该临界值，则表示这些参数组能够表征模型的功能特征。将低于该临界值的参数组的似然值赋为零，而将高于该临界值的所有参数组的似然值重新归一化，按照似然值的大小，求出在某置信度下模型预报的不确定性范围[19]。
GLUE包括以下几个步骤：（1）从均匀分布的可行参数空间中MC采样；（2）似然函数的说明和行为参数集阈值的解释；（3）计算行为参数集的似然值；（4）重新衡量这些值，算出累积分布；（5）从分布中对不确定性值求导。在这种方法中，似然值作为每个参数集的相对权重，或者模拟值。值得注意的是这些似然函数和阈值都是主观决定的。在本文中，NashSutcliffe 效率（ME）作为如下似然函数：
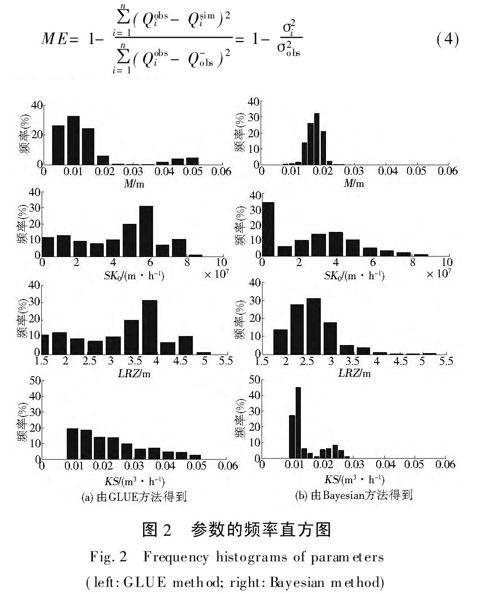
式中：Q-obs代表观测流量的均值（m3/s）；σ2i是第i个模拟的误差方差；σ2obs是观测方差。
3 结果
3.1 参数的不确定性
为了比较GLUE方法和Bayesian方法，选用TOPMODEL中四个较为敏感的参数，即M、SK0、LRZ、KS。每个参数都有一个明确的范围，在Bayesian 方法中，每个参数是多元的，一些参数可以同时迭代，所以采用正态分布采样，而GLUE方法只能从有效参数空间中得到样本，所以采样均匀分布。
本文用1998年5月1日8时到1998年8月31日20时的降雨、径流以及蒸发数据作为输入数据。分别用GLUE方法以及Bayesian方法采样1 000组参数集进行模拟，结果表明通过参数的范围对每个参数有较好的模拟，也有不好的模拟。为了更直观的比较，做出每个参数的直方图（图2），所有的参数具有良好定义和单峰的后验分布。从这些分布中，参数估计对模型值是无歧义的，分布的形状表明估计的不确定性的次数，参数在某一值处的频率越高说明参数的良好性，参数在某一值处的频率越低说明参数具有越多的不确定性。从图2可以看出，由Bayesian方法得到的参数后验分布的范围更窄，对应的频率也高，表明这种方法具有较好定义的参数和较小的不确定性。
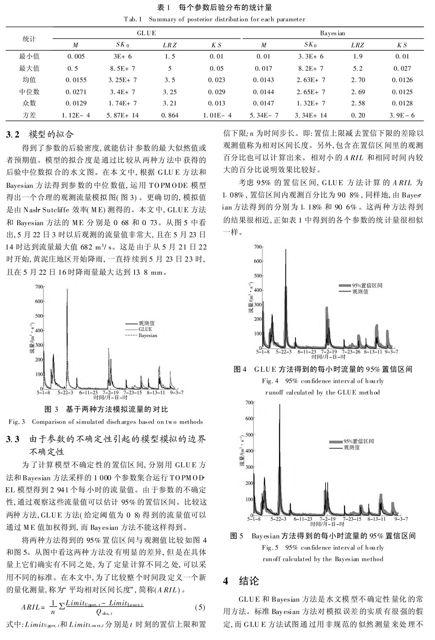
表1给出了参数的方差样本，代表对每个参数的后验总体统计。首先，GLUE方法和Bayesian方法有相似的参数空间；第二，两种方法中对应参数的均值没有很大的差异，同时也给出了每个参数的中位数和众数，在这三个量中，两种方法的众数是相差很小的。第三，尽管两种方法中每个参数的方差很小，但是也能观察出它们的区别，从表中我们可以看出由Bayesian 方法产生的样本有较小的离散性。第四，对于每个参数的取值范围，由GLUE方法得到的参数的区间长度比由Bayesian 方法得到的稍微大些。
3.2 模型的拟合
得到了参数的后验密度，就能估计参数的最大似然值或者预期值。模型的拟合度是通过比较从两种方法中获得的后验中位数拟合的水文图。在本文中，根据GLUE方法和Bayesian方法得到参数的中位数值，运用TOPMODE模型得出一个合理的观测流量模拟图（图3）。更确切的，模拟值是由Nash-Sutcliffe效率（ME）测得的。本文中，GLUE方法和 Bayesian方法的ME分别是0.68和0.73。从图5中看出，5月22日3时以后观测的流量值非常大，且在5月23日14时达到流量最大值682 m3/s。这是由于从5月21日22时开始，黄泥庄地区开始降雨，一直持续到5月23日23时，且在5月22日16时降雨量最大达到13.8 mm。
3.3 由于参数的不确定性引起的模型模拟的边界
不确定性 为了计算模型不确定性的置信区间，分别用GLUE方法和Bayesian方法采样的1 000个参数集合运行TOPMODEL模型得到2 941个每小时的流量值。由于参数的不确定性，通过观察这些流量值可以估计95%的置信区间。比较这两种方法，GLUE方法（给定阈值为0.8）得到的流量值可以通过ME值加权得到，而Bayesian方法不能这样得到。
将两种方法得到的95%置信区间与观测值比较如图4和图5。从图中看这两种方法没有明显的差异，但是在具体量上它们确实有不同之处，为了定量计算不同之处，可以采用不同的标准。在本文中，为了比较整个时间段定义一个新的量化测量，称为“平均相对区间长度”，简称（ARIL）。
式中：LimitUpper，t和LimitLower，t分别是t时刻的置信上限和置信下限；n为时间步长。即：置信上限减去置信下限的差除以观测值称为相对区间长度。另外，包含在置信区间里的观测百分比也可以计算出来。相对小的ARIL和相同时间内较大的百分比说明效果比较好。
考虑95%的置信区间，GLUE方法计算的ARIL为1.08%，置信区间内观测百分比为90.8%，同样地，由Bayesian方法得到的分别为1.18%和90.6%。这两种方法得到的结果很相近，正如表1中得到的各个参数的统计量很相似一样。
4 结论
GLUE和Bayesian方法是水文模型不确定性量化的常用方法。标准Bayesian方法对模拟误差的实质有很强的假定，而GLUE方法试图通过用非规范的似然测量来处理不确定性估计。目前，关于这两种方法的数学理论和结果在水文界引起了激烈的争论。由于它们的方法不同，所以对于这样的争论很难给出明确的结论。
本文针对中国淮河史灌河的黄泥庄流域通过TOPMODEL模型用GLUE和Bayesian方法分析参数的不确定性和模拟的不确定性，同时，也对比了这两种方法的效率和讨论了它们结果的不同之处。具体结论如下：（1）由Bayesian方法得到的参数样本比GLUE方法得到的离散性小；（2）对模拟流量的不确定性，给定GLUE方法的阈值为0.8的情况下，由Bayesian方法得到的置信区间与GLUE方法得到的置信区间很接近，这说明研究的参数后验密度函数的形状对最终结果的影响是有限的。
参考文献（References）：
[1] Kuczera G，Parent E.Monte Caro assessment of parameter uncertainty in conceptual catchment models：the Metropolis algorithm[J].Journal of Hydrology，1998，211：69-85.
[2] Jiang T，Chen Y D，Xu C Y，et al.Development and testing of a simple physically-based distributed rainfall-runoff model for storm runoff simulation in humid forested forested basin[J].Journal of Hydrology，2007，336：334-346.
[3] Refsgaard J C，Storm B.Construction calibration and validation of hydrological models.In：Abbott，M.B，Distributed Hydrological Modelling[J].Water Science and Technology Library，1996，22：41-54.
[4] Xu C Y，Tunemar L，Chen Y D，et al.Evaluation of seasonal and spatial variations of conceptual hydrological model sensitivity to precipitation data errors[J].Journal of Hydrology，2006，324：80-93.
[5] Engeland K，Xu C Y，Gottschalk Lars.Assessing Uncertainties in a conceptual water balance model using Bayesian methodology[J].Hydrological Sciences Journal，2005，50（1）：45-63.
[6] Marshall L，Nott D，Sharma A.Towards dynamic catchment codelling：a Bayesian hierarchical modeling framework[J].Hydrological Processes，2007，21：847-861.
[7] Kavetski D，Franks S，Kuczera G.Confronting input uncertainty in environmental modeling[J].In：Gupta H.V，Sorooshian S，Rousseau A.N，Turcotte R.Calibration of Watershed Models.AGU Water Science and Applications Series，Duan，2002，49-68.
[8] Chowdhury S，Sharma A.Mitigating parameter bias in hydrological modeling due to uncertainty in covariates[J].Journal of Hydrology，2007，340：197-204.
[9] Freer J，Beven K J，Ambroise B.Bayesian estimation of uncertainty in runoff prediction and the value of data：an application of the GLUE approach[J].Water Resources Research，1996，32：2161-2173.
[10] Beven K J，Feer J.Equifinality，data assimilation，and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology[J].Journal of Hydrology，2001，249（1-4）：11-29.
[11] Bates B C，Campbell E P.A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling[J].Water Resources Research，2001，37：937-947.
[12] Blasone R S，Madsen H，Rosbjerg D.Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling[J].Journal of Hydrology，2008，353：18-32.
[13] Vrugt J A，Braak C J F，Gupta H V，et al.Equifinality of formal（DREAM）and informal（GLUE）Bayesian approaches in hydrologic modeling Stochastic Environmental Research and Risk Assessment[C].2008，44，doi：10.1007/s00477-008-0274.
[14] Beven K J（马骏，刘晓伟，王庆斋，等译）.降雨-径流模拟[M].北京：中国水利水电出版社，2006.（Beven K J（MA Jun，LIU Xiao-wei，WANG Qing-zhai，et al）.Rainfall-Runoff Modelling[M].Beijing：China WaterPower Press，2006.（in Chinese））
[15] Chib S，Greenberg E.Understanding the Metropolis-Hastings algorithm[J].The American Statistician，1995，49：327-335.
[16] Beven K J，Binley A.M.The future of distributed models：models：model calibration and uncertainty prediction[J].Journal of Hydrology，1992，6：41-51.
[17] LuLi，JunXia，ChongYuXu.Evaluation of the subjective factors of the GLUE method and comparison with the formal Bayesian method in uncertainty assessment of hydrological model[J].Journal of Hydrology，2010，3：210-221.
[18] Z.Y.Shen，L.Chen，T.Chen.Analysis of parameter uncertainty in hydrological and sediment modeling using GLUE method：a case study of SWAT model applied to three Gorges Reservoir Region，China[J].Hydrol.Earth.Syst.Sci.，2012，16：121-132.
[19] Vahin Nourani.Arash Roughani.Mekonnen Gebremichael.TOPMODEL capability for rainfall-runoff modeling of the AMMAMEH watershed at different time scales using different terrain algorithms[J].Journal of Urban and Environmental Engineering，doi：10.4090/juee.2011.v5n1.001014.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/10 21:01:39