网站首页  词典首页

标题	试论初中数学勾股定理教学与学生知识串联能力培养
范文	施美霞 [摘 要] 勾股定理是初中数学教学的重要定理，是培养学生知识串联能力的有效工具. 本文从勾股定理串联数字运算、串联几何证明、串联函数演算三方面，具体阐释初中数学如何利用勾股定理教学推动学生知识串联能力培养. [关键词] 初中数学；勾股定理；知识串联 初中数学新课程标准对学生学习能力、创新能力都提出了全新的、更高的要求，而对学生学习能力和创新水平产生直接影响的则是学生的知识串联能力. 所谓知识串联能力，简而概之，便是学生举一反三，有效联系各类知识，形成强有力的知识正迁移，有效促进学生课程学习的一种能力. 初中数学知识学习在所有初中学科中是最成体系、最富结合度的，各个知识点串联运用的频率高、范围广，因此学生的知识串联能力对于初中数学的教、学同样具有重大意义. 勾股定理是解释直角三角形三边关系的重要定理，同时也是初中数学课程中最为重要的几个定理之一. 勾股定理具有形式变化多、应用范围广等特点，能与代数运算、图形推导、函数演算等数学内容进行串联应用. 基于这一特性，勾股定理便成为初中数学培养学生知识串联能力的极为有效的工具. 为了进一步培养学生的知识串联能力，推动初中数学课程改革，笔者就初中数学勾股定理教学如何与学生知识串联能力培养“擦出火花”进行探究，总结出如下三点建议. 勾股定理串联数字运算，培养 学生的代数运算能力 代数是初中数学非常重要的内容，包含有理数、整式、实数的代数运算，等式、不等式、方程等内容，是学生开拓初中数学知识时必不可少的工具. 将勾股定理及逆定理与代数知识内容进行串联，将为初中数学代数练习注入新鲜血液，将极大地丰富初中代数运算练习的内容与形式，有助于激发学生代数练习热情，提升学生代数综合解析、运算能力. 初中数学代数运算要与勾股定理有效串联，笔者认为要做好“换”的文章. 怎么“换”？就是将代数运算中的必备条件、必要数字、必定过程勾股定理化，将这些本来现成的代数运算条件全部换成勾股定理内容，让学生的代数运算能力在勾股定理和代数运算概念的灵活转化中得到提升. 应用题是数学运算中非常经典的表达形式，笔者将勾股定理串联到代数应用题中，设计了这样一道试题：“某条高速公路的快车道规定时速不能超过120 km/h，已知一辆小汽车沿着一段直道高速公路的快车道行驶，在路过车辆测速仪正前方时，汽车与测速仪相距60 m，2 s后，汽车距离测速仪100 m，请问汽车超速了吗？”要求汽车是否超速，就必须求出汽车的时速，这是一道典型的代数应用题，但这道代数题却把学生难住了，因为要求速度，必须知道路程和时间，时间是知道了，路程呢？于是笔者引导学生根据题意画了一张图（如图1）. 学生可以发现，汽车正对测速仪时刚好在A点，2 s之后，汽车在B点，测速仪和A，B两点刚好围成一个直角三角形，测速仪到A点的距离是60 m，到B点的距离是100 m，由此很容易得出AB2=1002-602，即AB=80 m. 由此可知小汽车的时速是80÷2=40 m/s=144 km/h，显然汽车已经超速了. 像这样利用勾股定理与代数运算串联，能有效培养学生分析问题、转化问题、解决问题的能力. 勾股定理串联几何证明，培养 学生的图形解析能力 三角形证明几乎占据了初中数学几何证明中的绝大部分内容，而勾股定理又是体现直角三角形三边关系、解决三边问题的有效定理，因此，勾股定理与初中数学几何证明可以说是无缝对接. 通过勾股定理的延伸运用，将为学生的几何证明打开一个全新的思路，许多看似难解、难证的几何问题，也将在勾股定理的引进和串联下迎刃而解. 勾股定理和初中数学几何证明之间的串联，笔者觉得其关键是“找”，教师要引导学生找到几何图形中潜在的勾股定理，并准确地把握勾股定理与图形证明之间的关系，从而解决证明问题. 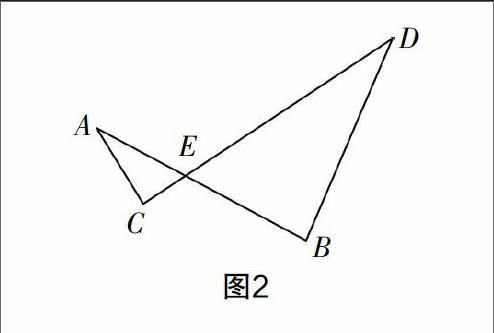例如，笔者为了将勾股定理与相似三角形证明进行串联，设计了这样一道试题：“如图2所示，AB与CD相交于点E，已知AB=11，AE=5，CD=13，DE=10，AC=4，DB=8，求证：△ACE∽△DBE.”学生一看此题，都一筹莫展，于是我开始引导学生：“同学们，我们知道AB=11，AE=5，那能不能求BE的长？”学生回答“能”，我再问：“那我们知道CD=13，DE=10，能不能求CE的长？”学生也点头说“能”，我接着引导：“同学们，经过计算后，我们手头掌握的条件如下，在△ACE中，AE=5，AC=4，CE=3，根据这组数字我们可以发现，AC2+CE2=AE2，符合勾股定理，所以△ACE是直角三角形；再看看△DBE，DE=10，DB=8，BE=6，根据这组数据我们可以发现DB2+BE2=DE2，符合勾股定理，所以△DBE是直角三角形. ”通过这样的引导，学生在图形解析时，利用勾股定理打开了突破口，能找到图形之间的联系，最终解决几何证明题，这有助于培养学生的发散思维，增强学生的图形解析素养，提升学生的几何证明能力. 勾股定理串联函数演算，培养 学生的抽象思维能力 对于很多学生来说，函数就是噩梦，缘何如此？答案就是函数太抽象了. 我们生活在一个具象的世界，对于事物都习惯用具象思维思考，所以很多学生才会对抽象化的函数演算产生畏难情绪. 函数是难，但并非毫无“破绽”，如果能够引导学生有效串联勾股定理，许多函数问题都能不攻自破. 因为函数是直角坐标系中的一组变量关系，在直角坐标系中我们很容易找到直角三角形，所以只要能在勾股定理和函数之间建立联系，解决函数问题自然不在话下. 那如何建立联系？笔者认为答案就一个字，那就是“变”. 很多时候，函数直角坐标系中没有直角三角形，这个直角三角形需要我们利用函数知识进行合理转化，自己“变”一个出来，只要能够引导学生顺利“变”出直角三角形，便能实现勾股定理与函数演算的有机串联. 比如，笔者在教学初中数学“一次函数”时，是这么引导学生串联勾股定理的，题目是：在直角坐标系中，有A（4，2），B（1，3）两点，点E是x轴上一点，求AE+BE的最小值. 这样的题目很抽象，学生不知从何下手，于是笔者引导学生：“同学们，我们学过的知识中，涉及最短距离的定理是什么？”学生思考后回答：“两点之间，线段最短. ”我说：“同学们说得很好，所以要求AE+BE的最小值，我们就应该使AE和BE变成一条线段. 最简单的方法是什么？设置点A关于x轴对称的点A′（4，-2）. ”学生点头，笔者继续引导：“我们现在有一条直线了，那我们好好观察一下，如果我们要变出一个直角三角形，A′B会是什么边？”“斜边”，学生齐答. 笔者点头继续引导：“所以，我们要变出一个直角三角形，只要找到两条直角边就行了，最简单的方法就是作BC∥y轴，A′C∥x轴，交点是C，于是点C的坐标是（1，-2）. 所以A′C=3，BC=5，A′B2=32+52，可得AB=.这样我们就求出AE+BE的最短距离了.”通过这样引导学生设置对称点，画平行线，“变”出一个直角三角形，将有助于帮助学生找到抽象思维具象化表达的方法，为学生破解抽象函数打通一条通道. 总之，利用初中数学勾股定理推动学生知识串联能力培养的核心思路，就是帮助学生养成思维发散习惯，引导学生在题干中找到隐藏着的解题之匙，通过知识之间的有机串联、组合和应用，提高数学学习效率. 教师一定要以此为突破口，多思多想，反复琢磨，探索更多勾股定理与其他知识点有效串联的策略，真正用好勾股定理，提升学生知识联系能力和综合运用能力，切实推动初中数学教学.
随便看	浅议现代“美文”入门创作三部曲 浅谈新基础教育视域下初中作文教学对“学生立场”的关照 中国画融入高中诗词意境教学初探 如何培养农村中学生语文课外阅读的兴趣 新课标下小说整本书阅读教学方法初探 高中议论文教学纵横式序列化训练模式浅析 浅谈近几年高考考场作文命题类型 浅谈在高中语文教学中培养学生核心素养的有效途径 我心中的那轮明月 挫折是特殊的礼物 新课标，让我放飞理想 浅谈信息时代的语文阅读教学 古典诗歌单元阅读拓展整合课堂初探 高中古典诗歌学案导学模式研究 细读：直抵大师心魂 巧架学科网络　构建知识体系 诗词 我是这样引导学生读写古诗词的 深耕金镶玉 巧解名句题 概要写作 浅议新课标下的高中古文教学 如何活跃小学语文课堂气氛 以教材为载体，有效进行人文素养培养 借兴趣之翼，助语文快乐飞翔 引导学生写日记之妙招 extending extend over ex-tends extends extend/stretch extension extensionalism extensionalisms' extensionalisms extensionality's extension cord extension lead extensions' extensions extension strategy extensionstrategy extensive extensively extensiveness extensivenesses extensiveproblemsolving extensivities extensivity extent extents 衰替 衰月 衰服 衰朽 衰朽的力量 衰朽的老翁 衰杀 衰条 衰枯 衰次 衰歇 衰歇沦谢 衰止 衰残 衰残的样子 衰气 衰沮 衰泪 衰涕 衰渐 衰灭 衰灯 衰疲 衰疲委顿 衰疾

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。