《直角与一线三等角在几何和代数中的初步应用》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

直角与一线三等角在几何和代数中的初步应用

范文

夏满

【摘要】在之前的文章中，我提到了一线三等角的模型，然而知道模型和构造模型，从知识体系和能处理的问题上来说，还是有很大的区别.想要解决更加复杂的几何或代数问题，构造一线三等角是初中阶段学习数学不可或缺的一部分.本文将从三方面阐述，希望对广大学子有所帮助.

【关键词】直角;认识和构造一线三等角;一线三等角的运用

一、引入：借助直角构造一线三等角

1.如图1，△ABC为含30°角的直角三角形.

做法：（1）平面内，在△ABC三边所在的直线外任选一点D，连接BD;

（2）过点A、点C作AE，CF垂直BD，分别交于点E、点F，如图2，3.

结论：由于点D的位置选择的不同，得到的模型的形状也就不一样，但总有△AEB与△CFB相似，判定理由为AAA.

2.如图4，△ABC为含45°角的直角三角形

做法：同上，如图5，6.

结论：由于点D的位置选择的不同，得到的模型的形状也就不一样，但总有△AEB与△CFB全等，判定理由为AAS.

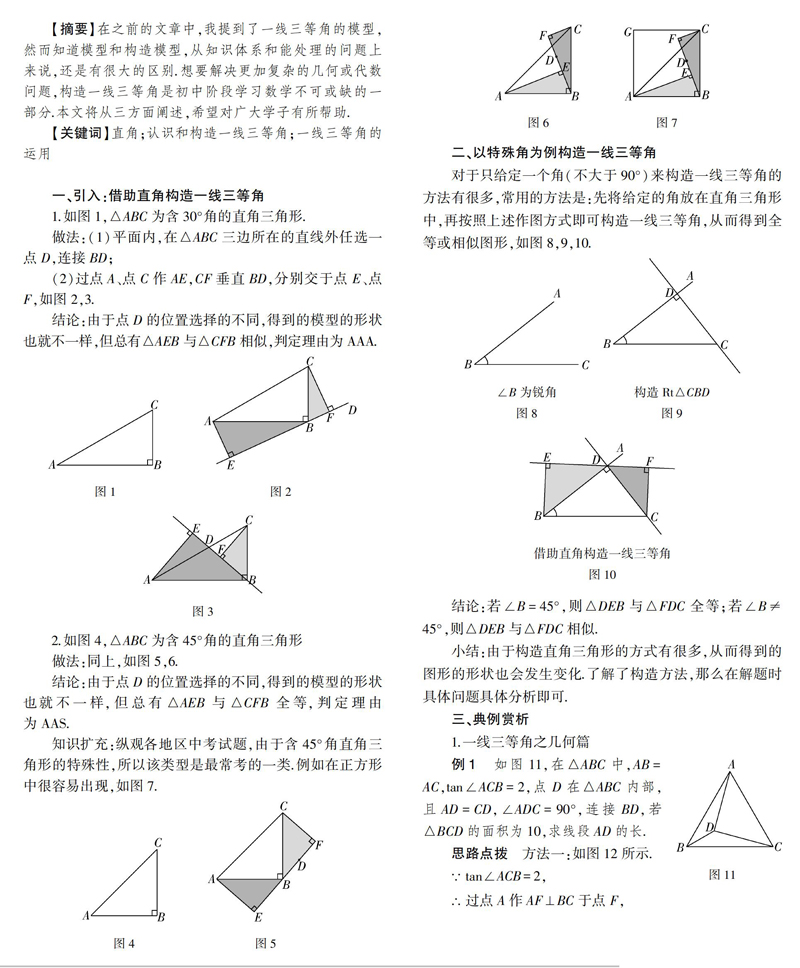
知识扩充：纵观各地区中考试题，由于含45°角直角三角形的特殊性，所以该类型是最常考的一类.例如在正方形中很容易出现，如图7.

二、以特殊角为例构造一线三等角

对于只给定一个角（不大于90°）来构造一线三等角的方法有很多，常用的方法是：先将给定的角放在直角三角形中，再按照上述作图方式即可构造一线三等角，从而得到全等或相似图形，如图8，9，10.

∠B为锐角

借助直角构造一线三等角

结论：若∠B=45°，则△DEB与△FDC全等;若∠B≠45°，则△DEB与△FDC相似.

小结：由于构造直角三角形的方式有很多，从而得到的图形的形状也会发生变化.了解了构造方法，那么在解题时具体问题具体分析即可.

三、典例赏析

1.一线三等角之几何篇

图11例1 如图11，在△ABC中，AB=AC，tan∠ACB=2，点D在△ABC内部，且AD=CD，∠ADC=90°，连接BD，若△BCD的面积为10，求线段AD的长.

图12思路点拨方法一：如图12所示.

∵tan∠ACB=2，

∴过点A作AF⊥BC于点F，∴AFFC=2.

∵AB=AC，AF⊥BC，∴BF=CF.

设CF=x，则BF=CF=x，BC=2CF=2x，AF=2FC=2x，∴AC=5x，

∴AD=AC2=102x.

又∵S△BCD=10，

∴过点D作DE⊥BC于点E，则DE=10x.

∵AD=CD，∠ADC=90°，

∴过点D作DH∥BC交AF于点H，过点C作CG⊥DH于点G（构造一线三等角），

∴△ADH≌△DCG（AAS），∴DH=CG，AH=DG.

又∵DE=CG，

∴四边形DEFH为正方形，四边形HFCG为矩形，

图13∴DH=DE=HF=10x，HG=FC=x，

∴AH=AF-HF=2x-10x，

DG=DH+HG=10x+x，

∴2x-10x=10x+x，解得x=25，

∴AD=102x=102×25=52.

方法二：本题还可以按照图13构造一线三等角来解决.

图14例2 如图14，在△ABC中，AB=AC，∠BAC=90°，∠EPF=90°，顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，连接AP交EF于点G，求证：四边形AEPF的面积是△ABC的一半.

图16思路点拨方法一：如图15所示.

∵AB=AC，∠BAC=90°，点P是BC的中点，且∠EPF=90°，

∴△EPA≌△FPC（ASA），

∴△EPF为等腰直角三角形.

过点E作EM⊥BC，过点F作FN⊥BC，则△EMP≌△PNF（ASA）.

过点E作EH⊥AP，过点F作FI⊥AP，则△EPH≌△PFI（ASA），

∴△EMP，△PNF，△EPH，△PFI均全等，

∴EM=FI，EH=FN.

∵S△BEP=12BP·EM，S△APF=12AP·FI，又∵BP=AP=PC，

∴S△BEP=S△APF，

同理可得S△AEP=S△CFP.

∵S四边形AEPF=S△AEP+S△APF，S△ABC=S四边形AEPF+S△BEP+S△CFP，

∴S四边形AEPF=12S△ABC.

方法二：如图16，可通过证明△BPE≌△AFP（ASA），△EPA≌△FPC（ASA），

得到结论.

2.一线三等角之代数篇

例3 如图17，在平面直角坐标系xOy中，点P为抛物线y=x2上一动点，点A的坐标为（4，2）.在抛物线上是否存在一点P，使∠AOP=30°？若存在，请求出点P的坐标.

分析将特殊角放在直角三角形中，构造一线三等角得到相似或全等三角形解决问题.

思路点拨

如图18所示，假設存在这样的点P，连接OP并延长.

过点A作AG⊥OA，交OP于点G，则△OGA为含30°角的直角三角形，AGOA=tan 30°=33.

过点A作AC⊥x轴于点C，过点G作GH⊥AC于点H，则△AGH与△OAC相似，∴GHAC=AHOC=AGOA=33.

设点G（a，b），则H（4，b）.∵A（4，2），

∴GH=4-a，AC=2，AH=b-2，OC=4，

∴4-a2=b-24=33，解得a=4-233，b=433+2，∴点G的坐标为4-233，433+2，

∴OG的函数解析式是y=（2+3）x.

联立y=（2+3）x与y=x2，得到的解即为点P的横坐标.

小结：由于构造直角三角形的方式很多，故作图方法不唯一，但总体应保持思路一致.

【参考文献】

陈汝作，钱耀邦.初中数学解题技巧[M].上海：东方出版中心，1998.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。