《基于MCMC方法的船舶柴油机磨损故障分布研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于MCMC方法的船舶柴油机磨损故障分布研究

范文

李彦强　江杰

摘要：该文借助WINBUGS软件运用MCMC（MarkovChainMonteCarlo，马尔科夫链蒙特卡洛）估计方法，采用Gibbs抽样原理，在贝叶斯理论的框架下，结合某船舶柴油机气缸盖历史的和更新的磨损故障时间数据，有效提高了磨损故障概率分布的精度。首先介绍了柴油機对船舶航行安全的重要性及其常见故障类型，确定了采用贝叶斯框架下的MCMC抽样方法对磨损故障分布进行仿真计算；其次阐述了通过最大似然估计法获得先验分布参数的过程，并说明了MCMC方法的原理及其常用的抽样方法；最后，引

WINBUGS软件并采用此软件进行建模分析，进行基于Gibbs抽样的MCMC方法的柴油机磨损故障分布计算，以实际算例证明此方法提高了柴油机磨损故障概率分布的计算精度。

关键词：柴油机；磨损故障；贝叶斯网络；MCMC；WinBUGS

中图分类号：TP311

文献标识码：A

文章编号：1009-3044（2017）10-0190-05

1.概述

柴油机是船舶动力装置的关键设备，一旦其发生故障，将会严重影响船舶的正常运行，并有可能直接或间接地造成无法估量的经济损失，甚至可能损坏其他关键设备，严重时还会危及到船员和旅客的人身安全。船舶柴油机的工作环境和条件往往多变而恶劣，由于不稳定的环境与人为操作，船舶柴油机常在负荷与转速多变的工况下运转。柴油机的结构复杂性决定了柴油机故障类型的复杂性，负荷与转速多变又会直接导致柴油机的许多零部件常处于高温、高压、高速的环境下工作，加之人为因素导致的润滑不足、操作不规范等，柴油机零部件故障多发、复杂，具有不确定性和多样性。

船舶柴油机的故障按照子系统来分，主要分为喷油系统故障、燃料系统故障、涡轮增压系统故障、冷却系统故障以及润滑系统故障等。如果按照导致柴油机故障的原因来分类，那么主要有磨损、冲击振动、腐蚀、老化等。其中，磨损故障时柴油机的主要故障类型，约占船舶柴油机故障比率的37.5%t31。船舶柴油机磨损故障一旦发生，若没有及时、准确地排故和维修，就无法保障船舶动力装置的正常运行，甚至会导致严重的安全事故和经济损失。但是，过于频繁地对船舶柴油机进行检修，不仅会带来不必要的人为差错，还会导致维护费用急剧上升，不符合船舶管理的经济性要求。因此，掌握柴油机磨损故障的发生规律、合理地安排检修工作至关重要。

国内外在这一领域有不少相关研究，但大多集中在柴油机故障诊断技术可靠性分析方面，对磨损故障的具体分布研究不够细化，本文在这方面进行了一定的研究，结合MC-MC方法有效提高了船舶柴油机磨损故障分布的计算精度。

柴油机磨损故障的失效前平均时间（Mean Time To Fail-tire，MTI'F）的概率分布可以通过历史的统计数据获得，但由于船舶柴油机工作环境复杂多变，根据历史数据计算得出的概率分布仅能代表综合环境下的情况，对于近期具体的工作环境下的故障分布来说不够准确。如果能结合近期的MTTF数据，对由历史数据获得的柴油机磨损故障MTTF分布进行更新，就可以得到更加符合现有实际情况的概率分布，有效提高磨损故障发生的预测精度。

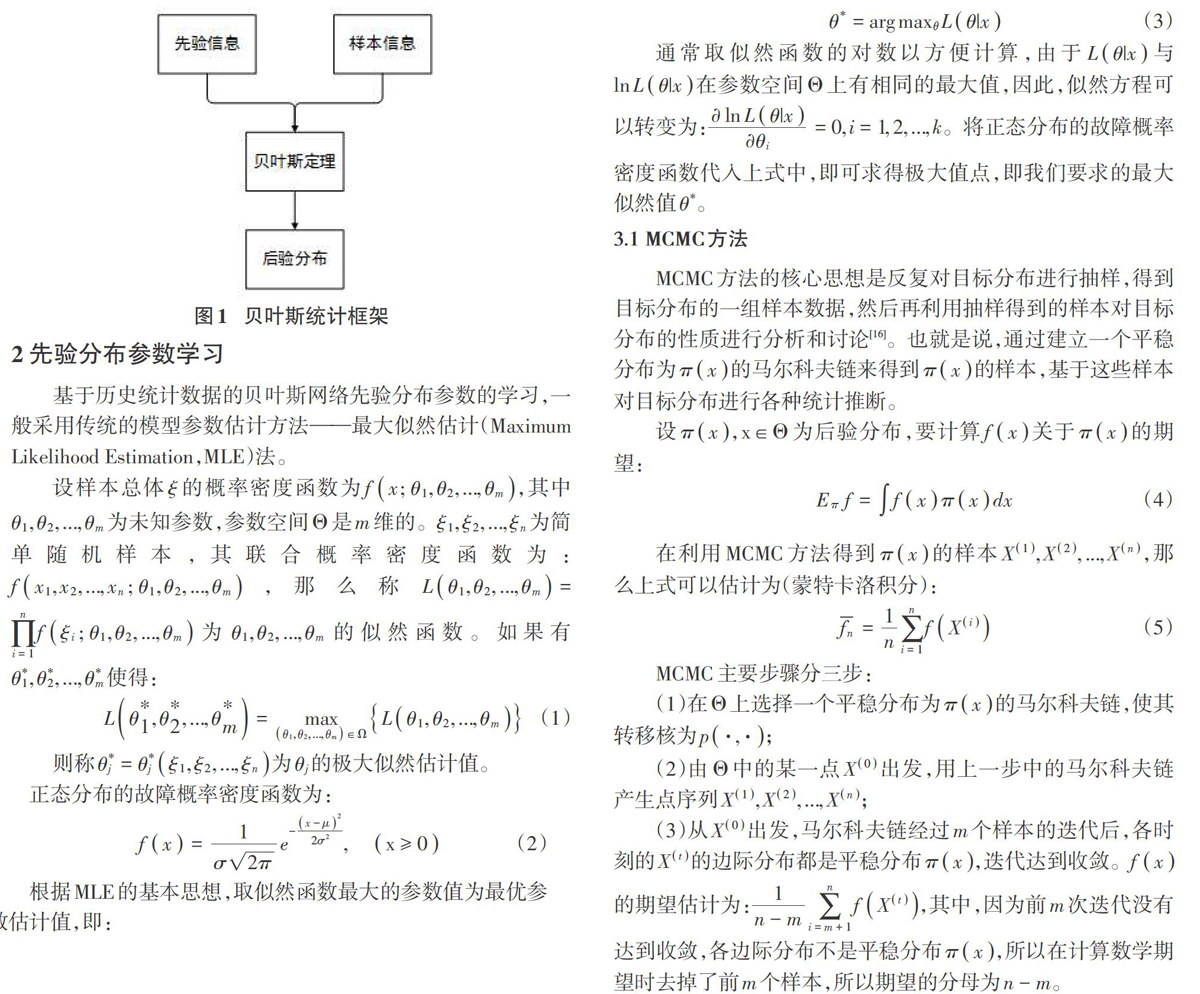
在信息更新方面，贝叶斯网络（Bayesian Network，BN）具有独特的优势。贝叶斯网络是表示随机变量间依赖和独立关系的网络模型，也称为贝叶斯网、因果概率网络或信念网络，它是一个有向非循环的图形结构，其中节点代表问题域的随机变量，节点间的有向边代表变量之间的直接依赖关系，每个节点都附有一个概率分布。贝叶斯定理可以结合先验信息和样本信息，获得更新的后验分布，提高预测精度，如图1所示。但是，贝叶斯统计的困难在于，后验分布是复杂的、高维的分布，难以进行直接计算，所以随着计算机技术与MCMC方法的发展，后验分布的计算被大大简化。

常见的船舶柴油机零部件故障分布规律有指数分布、正态分布、指数正态分布和威布尔分布。超载下工作或过热导致的柴油机故障、人为失误以及偶然操作不当引起的突发故障等均适用于指数分布的故障分布规律；由几种相对独立、作用均匀的微小差异量因素造成的零部件故障，如燃烧室组件、气缸和活塞等的磨损、喷油系统沉淀故障等，其故障概率分布函数大多为正态分布；油水系统和齿轮传动系统故障、滚珠轴承的磨损故障等服从威布尔分布规律。由于不同故障分布问题的在本文的研究方法下类似，所以，选取正态分布进行后续计算说明。

3.后验分布参数获取

在贝叶斯估计中，后验均值即为参数的估计。但在实际计算时，参数后验分布往往难以计算，解析法求解几乎不可能，计算量庞大而过程复杂。近十几年来，计算机技术高速发展，加之贝叶斯方法的不断改进完善，特别是MCMC方法以及Win-BUGS（Bayesian inference Using Gibbs Sampling）软件的发展和应用，原本复杂的高维计算问题可以通过从后验密度抽样取平均的方法方便快速地得到解决。原本传统蒙特卡洛的基本思想是，当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。在处理高维、复杂的问题时，MCMC方法相对于经典的蒙特卡洛方法有明显的优越性，可以在非标准形式、各变量之间互相不独立的情况下进行分布的模拟，在近十几年内被广泛应用于贝叶斯统计、显著性检验等方面。

3.1 MCMC方法

MCMC方法的核心思想是反复对目标分布进行抽样，得到目标分布的一组样本数据，然后再利用抽样得到的样本对目标分布的性质进行分析和讨论。也就是说，通过建立一个平稳分布为π（x）的马尔科夫链来得到π（x）的样本，基于这些样本对目标分布进行各种统计推断。

在MCMC方法中，可以根据转移核的不同构造方法，将主要的MCMC方法分为三种：

（1）Metropolis抽样

Metropolis抽样是最先被使用的MCMC方法，基本思想是从一个对称分布抽取样本，计算接收样本的概率，根据求得的概率值决定是否接收样本，再抽取新的样本，重复这个过程，直至收敛。

（2）Metropolis-Hastings抽樣

Hastings把最初的Metropolis抽样进行了进一步推广，不要求抽取样本的分布为对称分布。

（3）Gibbs抽样

Gibbs抽样是MCMC方法中应用最广泛的一种，它是Me-tropolis-Hastings抽样的一种特殊情况。

3.2基于WinBUGS软件的柴油机零部件磨损故障分布计算

WinBUGS是英国剑桥公共卫生研究所的MRC BiostatisticsUnit推出的用MCMC方法进行贝叶斯推理的专用软件包。WinBUGS可以方便快捷地对各种或常用或复杂的模型和分布进行Gibbs抽样，贝叶斯网络的各变量节点之间的关系也可以通过简单直观的有向图模型进行描述。除此之外，WinBUGS还可以给出指定参数的Gibbs动态抽样图，用Smoothing方法得到后验分布的核密度估计图、抽样值的自相关图等，这使得我们可以对马尔科夫链的收敛性进行直观的判断。参数后验分布的均值、标准差、蒙特卡洛平均标准误差（MC error）等信息也可以直接得到。

在解决柴油机磨损故障MTFF的分布计算问题时，可以按照以下几个步骤进行后验分布参数的估计：

1）建立Doodle模型并检验

在WinBUGS中，Doodle模型通过节点、箭头和平板等元素来进行构建。模型中的每个节点都具备相应的详细属性，在构建Doodle模型时就要指定每个节点的详细属性。

检验Doodle模型的目的是检验WinBUGS对所建立的模型是否识别，即检验建立的模型是否符合软件要求。当出现报错信息时，需要修正模型，直至显示"model is syntactically cot-rect”。

2）载人数据、模型编译和设定初始值

数据输入可以按照以下方式进行定义：

list（t=c（98，110，77，56，102，89，126，97，74，52），

x=c（6，16，54，3 3，25，4 68 890），N=10）

这种数据的表示格式被称为S-PLUS格式。当输入的数据为多维数组形式，具体的数据输入格式可以参照软件中的Help按钮，其中有进行详细的介绍。

当数据载入后，就可以通过Compile按钮继续进行模型的编译，对数据的完整性和一致性进行检验。最终，写入初始值，通过load inits按钮进行设定。

3）变量监控和模型迭代

在Inference选项中的Sample按钮下，设置所需监控的变量，逐个输入并set。接着在Update中输入迭代次数，进行模型迭代。

4）结果输出

在之前打开的样本监控工具窗下输入，便可以得到所有设置节点的运行结果。至此，一个模型的构建到运行结束。

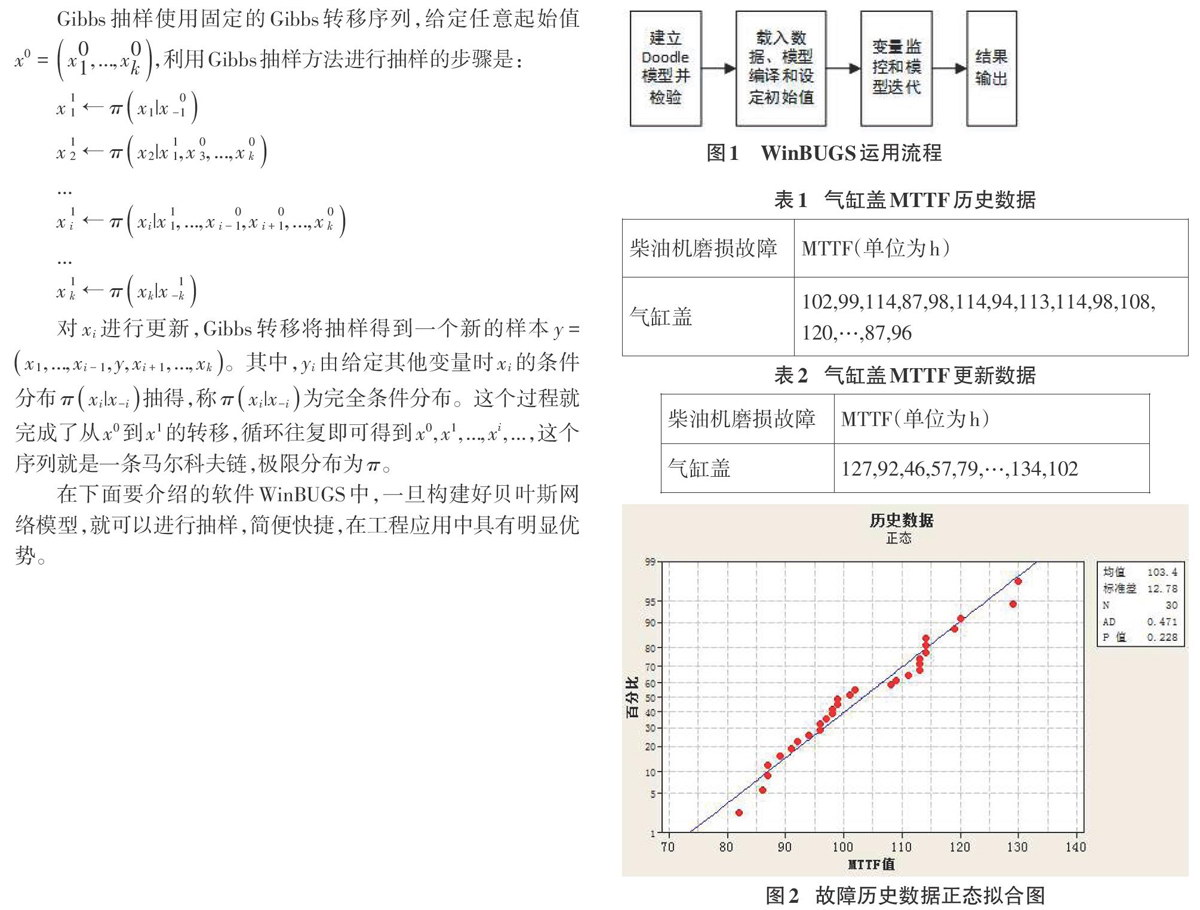
这四个步骤可以用图1来表示：

下面，本文将针对船舶柴油机气缸盖磨损故障的MTTF进行详细的算例说明，计算其更符合实际、更准确的概率分布。

4.实例应用

某船舶柴油机气缸盖磨损故障的MTYF历史数据与更新数据如表1、表2所示：

根据前面介绍的极大似然估计，利用现在最常用的质量管理统计Minitab，结合历史数据可以得出气缸盖磨损故障MTTF服从Normal（103.4，12.782），如图2所示：

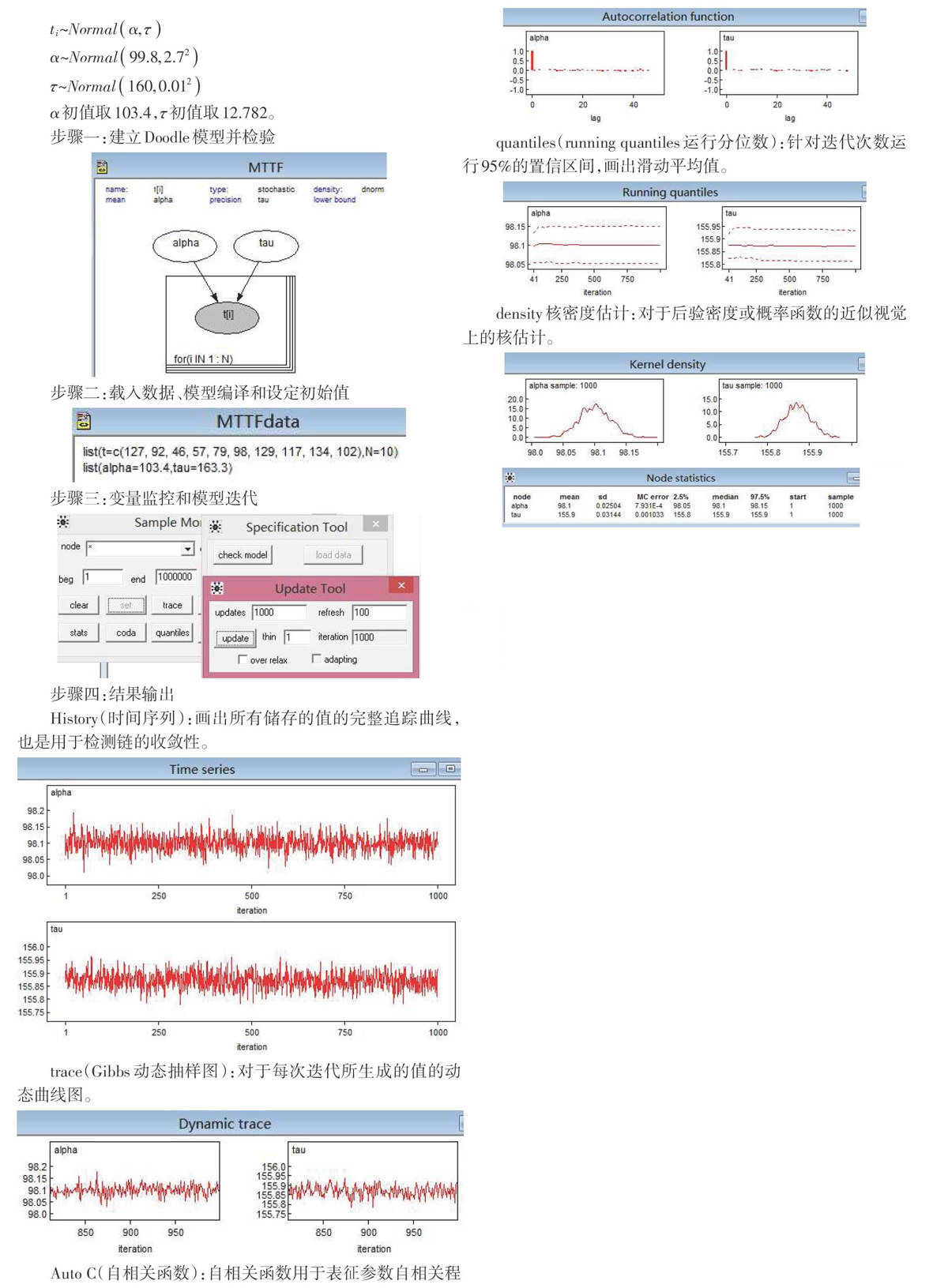
Auto C（自相关函数）：自相关函数用于表征参数自相关程度的大小，波动范围越大，表示自相关程度越大。可使用自相关图来检测收敛性，如果自相关程度低，那么在迭代次数较少时就已收敛。此处自相关程度较低，基本在迭代次数20以内就已收敛，故后验分布计算值可信。

stats中的mean代表所求节点的后验平均值，通俗来说就是我们要得到的结果。样本数据越多，后验估计越准确。可以计算每个参数的Monte Carlo error（蒙特卡罗标准平均误差）来评定后验估计的精度。一般来说，仿真应一直进行到参数的MC error小于样本SD的5%，即可满足精度要求。此处结果均满足精度要求。

综合以上，链的收敛性可以通过以下几步来进行判断：

1）初步可由history和trace所画的图来初步观察，若值在一个平行的区域内而没有强烈的季节性，那么链可能收敛，此处明显可能收敛；

2）通过auto C自相关函数进一步判断收敛性，此处自相关程度低，在迭代次数很少时就已收敛；

3）接着，可根据running quantiles运行分位数来判断收敛性，图中分位点稳定，暗示已收敛；

4）最后，根据stats中的MC error比对应的后验标准差要小很多，那么就可以认为链收敛。链收敛就说明后验密度被精确估计。

某船舶柴油机气缸盖磨损故障MTYF：

先验分布：Normal（103.4，12.782）

后验分布：Normal（98.1，12.492）

由图3可知，得到的后验分布更接近实际总体数据的分布，在只利用历史先验分布和更新数据的条件下提高了分布精度。近期实际运行中得到的MTYF更新数据对由历史数据得到的MTTF分布进行了修正，得到的后验分布更贴近目前的使用实际情况。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。