《基于改进的k-means算法的新闻聚类的研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于改进的k-means算法的新闻聚类的研究

范文

唐啸虎刘志锋

摘要：针对k-means聚类算法对初始聚类中心敏感，容易陷入局部最优的情况，提出一种改进的基于k-means算法的新闻聚类方法。在用传k-means算法对新闻数据集进行多次聚类的基础上，使用證据累积算法对k-means算法的聚类结果进行融合，以平滑k-means算法的结果，减少波动。实验结果表明提出的方法使聚类结果的准确率从53.33%提升至77.78%。

关键词：k-means;新闻;聚类分析;融合;分级聚类

中图分类号：TP391 文献标识码：A

文章编号：1009-3044（2020）10-0201-03

随着互联网的高速发展，人们已经迈向了一个信息化的时代，互联网上的信息交流和获取逐渐取代了传统的电视、报纸、书信等传统媒体。截至2019年6月，中国网民规模为8.54亿人，互联网普及率达61.2%，网站数量518万个。人们每天通过浏览器或者新闻APP看新闻产生大量点击记录，对人们点击的海量新闻进行分析，可以获知特定时间和特定范围内公众最关心的热门事件，进而可以在信息爆炸的互联网时代帮助人们更快、更好、更有效地获取有用的信息。如何快速、有效地在海量新闻浏览记录中发现其中的趋势和主题，不仅能够帮助个人更准确地了解全社会关注的热点事件，同时还能辅助国家及时发现网络舆情事件、趋势，在网络舆情分析、重大网络事件监测防御、信息网络安全等领域具有极其重要的现实意义。

聚类分析旨在分析数据过程中发现数据对象之间的相互关系，将数据依据一定原理进行分组，各分组结果内的相似性越大，各分组之间的差别就越大，聚类效果越好。k均值（k-means）聚类算法具有快速、简单的特点，对大数据集有较高的分析效率。

本文提出了一种结合k-means算法与分级聚类算法的方法，利用k-means算法对预处理过的新闻数据集进行多次聚类，然后用证据累积算法融合多次聚类得到的结果，减少波动。本文对搜狐新闻数据进行分析，考查本文方法的聚类效果，并与传统k-means算法的聚类效果进行比较，体现本文方法的优势。

1算法简介

1.1k-means算法

k-means算法采用迭代更新的思想，该算法的目标是根据输入的参数k将数据对象聚成k簇，其基本思想为：首先指定需要划分的簇的个数k值，随机地选择k个初始数据对象作为初始聚类或簇的中心;然后计算其余的各个数据对象到这k个初始聚类中心的距离，并把数据对象划分到距离它最近的那个中心所在的簇中，然后根据公式：

1.3 k-means算法优缺点

k-means算法是解决聚类问题的经典算法，这种算法简单快速。当结构集是密集的，簇与簇之间区别明显时，聚类的结果比较好。在处理大量数据时，该算法具有较高的可伸缩性和高效性。

但是，目前传统的k-means算法也存在着许多缺点：

（1）k-means聚类算法需要用户事先指定聚类的个数k值。在很多时候，在对数据集进行聚类的时候，用户起初并不清楚数据集应该分为多少类合适，对k值难以估计。

（2）对初始聚类中心敏感，选择不同的聚类中心会产生不同的聚类结果和不同的准确率。随机选取初始聚类中心的做法会导致算法的不稳定性，有可能陷入局部最优的情况。

1.4分级聚类算法

分级聚类是一种自底向上的聚类方法。它的主要思想是：首先将每个样本自定义为一类，然后逐步合并，直到最后聚为一类或者达到要求为止。

对于给定的n个样本集合x={x1，x2，...xn}，分级聚类方法的具体步骤如下：

（1）x中每个样本Xi均自成一类ci，这样就构建了一个初始聚类C={c1，c2，...，cn};

（2）计算c中每对类（ci，ci）之间的相似度sim（ci，cj）;

（3）选择最大相似度的类对Max（sim（ci，ci）），并将其合并为一个新类Ck-CiUci，构成一个新的聚类c={c1，c2，...，ck..，cn-1};

（4）如果C中只有一个类或C已经达到要求，则结束;否则转到（2）。

分级聚类实际上将产生一棵树，底部叶子结点代表n个样本，根结点为最后聚为一类的情况，中间的某层代表其中的一种聚类。

2改进的k-means算法

传统的k-means算法对初始聚类中心敏感，聚类结果随不同的初始聚类中心而波动。针对k-means聚类算法中随机选取初始聚类中心的缺陷，本文提出了一种改进的方法，步骤如下：

（1）准备好数据集D={d0，d1，d2，...，dn-1}，数据集中共有n条数据。

（2）对簇的数目k取2到19，对于每一次聚类结果，计算惯性权重，画出k值一惯性权重折线图，根据肘点法，选择最合适的簇的数目k1。

（3）使用k-means聚类算法对数据集进行多次聚类，每次聚类，k从区间[k1-m，k1+j]随机取值（m>0，j>0且m+j<8），每一次聚类完成后，遍历所有数据点所在簇的标签，簇标签集合为{0，1，2，3…，k-1}。

（4）记录具有相同标签的两个数据点的位置，创建共协矩阵：

（5）多次运行k-means算法，把每一次迭代得到的共协矩阵相加，矩阵中的数值表示两个数据点被分到同一簇的次数。

（6）使用分级聚类对第一步得到的共协矩阵进行聚类分析。构造共协矩阵的最小生成树。

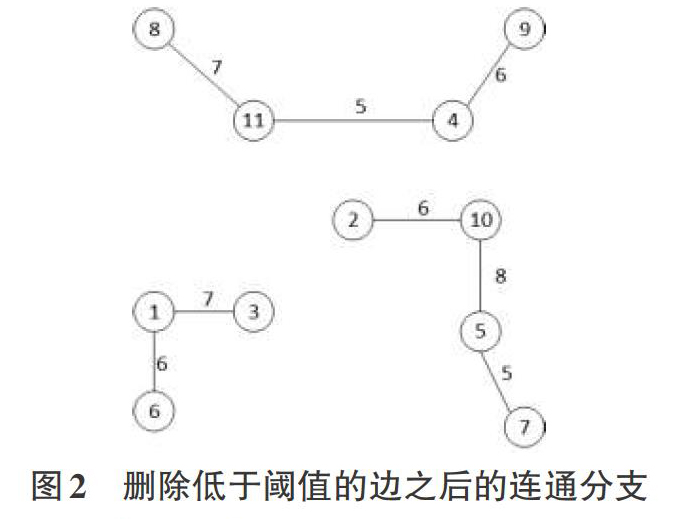
生成树中的节点对应数据集中的个体，边的权重对应两个节点被分到同一簇的次数，也就是共协矩阵所记录的值。

（7）遍历最小生成树矩阵中的每一条边，删除低于阈值的边。

（8）最后，找到所有连通分支，也就是寻找移除低权重边以后仍然连接在一起的节点。连通分支的数量就是簇的数量，连通分支中的节点就是被分到同一簇的数据。

3新闻数据聚类实验与结果分析

3.1实验数据集

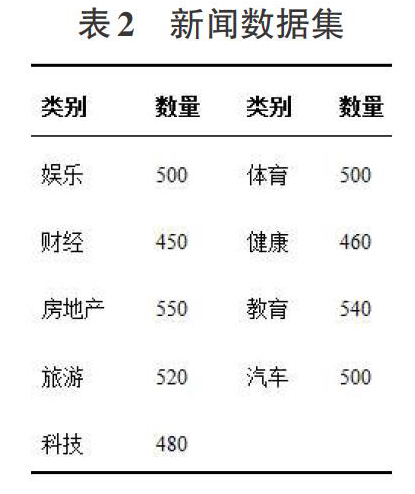
本文的实验数据集来源于网络搜狐新闻，数据集包含了9个类别的新闻：娱乐、财经、房地产、旅游、科技、体育、健康、教育、汽车，共4500条。新闻类别名与数量如下表所示。

3.2评价指标

本文的主要工作是提升新闻聚类的准确率，对于聚类产生的k个簇的新闻，采用准确率A来评价算法的正确性，准确率A的计算方法如下：

公式（3）中，Ca表示新闻数据集中所有新闻类别的集合，CK表示使用k-means算法聚类后得到的类别集合。

3.3实验分析

3.3.1实验过程

首先对数据集进行分词、去除停用词处理。本文采用了iieba分词工具对数据集进行分词，采用哈工大停用词表去除数据集中的停用词。

对经过分词、去除停用词预处理之后的4500条数据进行聚类，k依次取区间（2，20）内的值，每次运行算法都计算惯性权重。

图3中，横轴是k的值，纵轴是惯性权重。由折线图可知，随着簇数量的增加，质心点和其他数据点位置的调整逐渐减少，惯性权重逐渐降低。簇数量为9时，惯性权重进行了最后一次大的调整。

使用k-means算法对新闻数据集进行聚类，运行12次，每次k值在区间[6，12]上随机取值，将聚类结果保存到共协矩阵中。然后，将12次运行得到的共协矩阵相加，使用分级聚类算法对共协矩阵进行聚类分析，构造最小生成树，删除低于阈值的边后，连通分支就是聚类得到的各个簇。

对聚类结果中的每个簇，对该簇中的词语按权重由大到小排序，选取权重最大的10个词作为该簇关键词，聚类结果如下表所示。

对聚类结果进行分析，可以得出结论：本文所提出的基于k-means的聚类方法能够准确、有效地对新闻进行分类，获取的聚类中心附近的高频关键词可以较好地反映该簇所包含新闻的内容、主题、类别。

3.3.2对比分析

在同等条件下，用传统的k-means聚类算法对本文所使用的新闻数据集进行聚类分析。为保证结果的客观性，用传统k-means算法进行了5次聚类，取平均值作为最终结果，实验结果的对比如表4所示。

k-means算法对初始聚类中心敏感，选择不同的聚类中心會产生不同的聚类结果和不同的准确率。随机选取初始聚类中心的做法会导致算法的不稳定性，有可能陷入局部最优的情况。实验表明，与传统k-means聚类算法相比，本文使用证据累积算法对多次运行k-means算法得到的结果进行融合，能够平滑算法多次运行所得到的不同结果，可以减少波动。

综上所述，本文的方法在一定程度上降低了传统k-means算法对初始值的依赖，降低了算法的不稳定性，有效提高了算法聚类结果的准确率。

4结论

k-means聚类算法作为基于划分聚类算法的一个典型算法，在数据挖掘中被广泛应用，经常被用来作为预处理步骤。本文使用基于k-means算法的方法对新闻数据集进行聚类分析，以找到数据集中包含的新闻类别与主题。对新闻数据集进行分词、去除停用词预处理后，先使用k-means算法对新闻数据集进行多次聚类，然后使用分级聚类算法对运行k-means算法得到的多个结果进行融合，克服k-means算法因初始聚类中心的选择而导致的局部最优。实验证明本文的方法对聚类结果的准确率有较大提高。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。