《计算机藏式夹棋博弈系统中局面估值方法的研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

计算机藏式夹棋博弈系统中局面估值方法的研究

范文

尕藏扎西安见才让

摘? 要：局面估值或局面评估是计算机博弈系统的核心部分之一。良好的评估函数才能对局势作出客观的判断，较快地的找到最佳走法，让计算机博弈系统看得更准。针对藏式夹棋的博弈问题，提出一种结合藏式夹棋棋规的静态评估函数和结合MC的动态评估函数。对两种评估函数的准确率和效率进行了对比测试。

关键词：计算机博弈; 藏式夹棋; 静态评估; 动态评估

中图分类号：TP391.1? ? ? ? ? 文献标志码：A? ? ?文章编号：1006-8228（2019）09-61-03

Research on situation evaluation method in computer Tibetan chess game system

Gaznag zhaxi，? Anjian Cairang

（School of Computing，Qinghai University for Nationalities， Xining， Qinghai 810007， China）

Abstract： Situational valuation or situation assessment is one of the core parts of the computer game system. A good evaluation function can make an objective judgment on the situation， and ensure to find the best way to make the computer game system more accurate. Aiming at the game problem of Tibetan chess， this paper proposes a static evaluation function combined with Tibetan chess rules and a dynamic evaluation function combined with MC. The accuracy and efficiency of the two evaluation functions are compared and tested.

Key words： computer game; Tibetan chess; static evaluation; dynamic evaluation

0 引言

计算机博弈是人工智能研究的重要载体，也是目前最具挑战性的研究方向之一，人工智能的快速发展极大地推动了科技进步和社会发展[1]。国内外计算机围棋、国际象棋、亚马孙棋等等研究已成熟[2，9]。而计算机藏棋领域的研究才刚刚起步，还面临着很大的挑战。藏式夹棋搜索空间大、下棋规则多、盘面变化快。研究搜索藏式夹棋博弈和局面评估函数有很大的技术挑战和意义。与搜索算法一样，评估函数也是计算机博弈系统最核心的部分，它的好坏影响着今后局势的发展趋势。如果说搜索引擎是让程序看得更远，那么评估函数则是让程序看得更准。

本文根据藏式夹棋本身的规则，提出一种静态评估函数与MC算法结合的适合于藏式夹棋博弈系统的动态评估方法。可为实现较高博弈水平的藏式夹棋博弈系统打下基础。

1 藏式夹棋评估标准

1.1 子力

在藏式夹棋中，单个棋子来讲，每个棋子的作用都差不多，棋子的影响力更多的取决于它周围的环境，和该棋子连接或距离较近的己方棋子和空位置都是决定其影响力的因素，它会受哪些棋子的影响，这些棋子对它的影响力的范围值是多少，具体如何等。

1.2 位置

位于棋盘不同位置的棋子，即使其子力相同，其作用可能差别很大。在藏式夹棋中，棋子之间的相对位置是衡量其作用的一个关键。在棋盘中有些点是纵横线的交叉点和两个对角线的交叉点，因此这种点会影响八个方向或会受到八个方向的影响。而有的点只是对角线的交叉点或棋盘边线上的点，这些点的影响力相对较小。

1.3 機动

在藏式夹棋中，机动性的概念也有重要体现。藏式夹棋中的一块棋，如果周围有较开阔的扩展空间，或者可以方便地自己的其他棋块中间相夹对方棋快，那么其机动性就较高;反之，如果一块棋已被对方完全夹击，其机动性就很小。

2 藏式夹棋局面估值方法

在评估棋局盘面时，通常存在两个相互矛盾的因素：准确性高低与性能好坏。当评估越准确越全面时，计算机的博弈水平也自然而然的越高，但是时间对于博弈来说是很重要的约束条件，计算机博弈最好是既要保证一定的正确率来进行评估，也要尽可能多地访问局面数，同时，当评估考虑到的因素越细致，就越能提高其准确性，但是会消耗大量计算时间，访问的局面数就有所降低，从而影响搜索的深度与广度[3]。对计算机博弈当前盘面的评估方法分为：静态评估和动态评估。

2.1 静态局面评估方法

藏式夹棋是一种较复杂的棋类，因此直接从整体上进行判断或评估棋盘局面的话，其计算复杂性高而无法准确的判断。因此，分块组合是非常重要的一步。在本文中按棋规来各个规则分块组合;我们在进行评估之前先对棋规则做一个分块，然后再各个模块被充分评估后，将各个模块的评估结果综合起来，得出整个盘面的一个评估值。

2.1.1 进攻值

在藏式夹棋中进攻方法主要是夹法和打枪法两种。因此首先计算夹法的估值，在计算打枪法的估值。最后把两个估值综合起来，确定为最终的进攻值。夹法规则的估值计算公式如下：

[expJ=i=1nP（i）]? ⑴

[expJ]为夹法规则的进攻值，i为被夹的棋子号，n为被夹的总数。P（i）为对应棋子的价值。在藏式夹棋中每个棋子的作用都差不多，因此在这里每个棋子的价值定义为1。

打枪规则的估值计算公式如下：

[expQ=j=1mP（j）]? ⑵

[expQ]为打枪规则的进攻值，j为已打枪的棋子号，m为被打枪的总数。P（j）为对应棋子的价值（棋子的价值定义为1）。

按以上的夹法规则的进攻值和打枪规则的进攻值综合为藏式夹棋的进攻值。藏式夹棋的进攻值计算公式为如下：

[expJQ=i=1nP（i）+j=1mP（j）? ? Pi=1，Pj=1]? ⑶

2.1.2 威胁值

所谓威胁值，就是当轮到对手方行棋时，己方棋子被对手棋子吃掉的可能性评估，亦即我方棋子受到对方棋子威胁的评估值，也称对方对我方的威胁度。在藏式夹棋中对方对我方的威胁方式也是夹法和打枪法两种。对方用夹法来威胁的估值计算公式如下：

[axpJ=i=1nP（i）]? ?⑷

[axpJ]为对方用夹法规则来威胁的估值，i为对方夹我方的棋子号，n为被夹的总数。P（i）为对应棋子的价值。在评估函数时用来计算当前局面对我方有利的估值。因此，计算威胁值时，对方的每个棋子的价值设为-1。

对方用打枪规则威胁的估值计算公式如下：

[axpQ=j=1mP（j）]? ?⑸

[axpQ]为对方用打枪规则威胁的估值，j为对方已打枪的我方棋子号，m为被打枪的总数。P（j）为对应棋子的价值（棋子的价值定义为-1）。

按以上对方用夹法规则的威胁值和打枪规则的威胁值综合为藏式夹棋的威胁值。藏式夹棋的威胁值计算公式为如下：

[axpJQ=i=1nP（i）+j=1mP（j）? ?Pi=-1，Pj=-1]? ⑹

2.1.3 藏式夹棋的静态估值方法

按以上谈论，本文对藏式夹棋的静态局面估值方法用了分块组合的方法。首先计算了当前局面的进攻值，在计算当前局面对我方的威胁值。最后将进攻值和威胁值的综合后确定为当前局面的评估值。藏式夹棋的静态局面评估函数为如下：

[Evalboard=expJQ+axpJQ ]? ⑺

[expJQ]为当前局面的进攻值，[axpJQ]为当前局面的威胁值。

2.2 动态局面评估

评估算法其准确性将直接影响搜索算法的走向，也因此决定了博弈性能的优劣[7]。静态评估方法尽管具有一定的效果，但每个棋局的情况各不相同，应对方法也不同，不可能只采用某一固定法则去套用所有可能的情况，总会有例外出现，最重要的是，我们现在还没有找到一种非常准确的规则来能囊括所有可能遇到的问题[6]。通常决定静态评估算法好坏的关键是我们对要解决的问题有非常清晰的认识，只有充分了解问题所在，才可能通过编程来解决。针对这种情况，蒙特卡罗（Monte Carlo，简称为MC）算法就是一种可供考虑的方法，它通过对当前局面下所有可以选择的点进行大量模拟，得出胜负的统计概率，一般胜率较高的点就认为是可以选择的较好的点[5]。

MC算法用于藏式夹棋中的思想是：当我们给定一个棋局时，程序会在当前所有可落子的位置中随机选择，并不断重复这个过程，直到对弈结束，再把最终结果记录下来，作为对当前局面的评估依据，即通过尽可能多的统计模拟棋局的结果来评估当前局面的好坏。相对于静态评估，MC算法是一种动态搜索算法[4]。对于每个局面，可下的点最多不超过40个（棋盘上的交叉点总数），在这些点中可以比较容易的找到一些明显更好的点。因此，当模拟次数达到一定次的时候，只要恰当的选择函数，在这些较好的点上就会聚集大量的模拟。

MC算法的实现步骤如下：

Step1：选择。把当前盘面作为搜索树的根节点，在可以选择的节点中随机选择一个;

Step2：扩展。若该节点首次被选中，则将加入该点后的局面作为叶节点（没有子节点的节点）加入搜索树中，若该点并非首次被选中，则为该盘面作为子树的根节点再构建一次搜索树;

Step3：模拟。对当前棋局进行模拟，即随机下完整盘棋，模拟结束后，就可计算出根节点下每个子节点在模拟棋局中的获胜概率。

3 实验结果

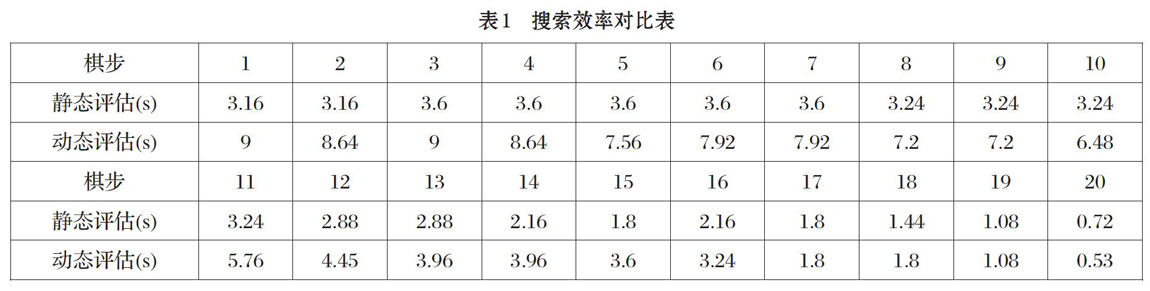
为了实验测试藏式夹棋静态评估与动态评估的搜索效率和准确率，将两种评估方法在搜索深度相同的前提下比较搜索效率和准确率。藏式夹棋在开局阶段搜索树较大，因此测试搜索效率时只有开局阶段的二十步。两种评估分别进行50局测试，并统计了开局阶段前二十步的平均时间和胜率，作为衡量两种评估方法在相同搜索深度中的搜索效率准确率。测试结果为表1和图1所示。

4 结束语

本文讨论了一种静态的藏式夹棋局面估值方法和基于MC的动态局面估值方法。两种方法有各自的优势与劣势。静态的估值方法有局限性，对局面的信息评估不全面、不准确。基于MC的动态估值方法对于搜索量巨大的局面，其收敛性很差，效率过低，耗时也很长。在后续的研究中，把基于MC的动态估值与静态的估值方法结合。寻求一种快速的、节省资源占用的，准确的估方法是未来研究的主要目标[10]。

参考文献（References）：

[1] 刘知青.现代计算机围棋基础[M].北京邮电大学出版社，2011.

[2] 于永波.基于蒙特卡洛树搜索的计算机围棋博弈研究[D].大连海事大学，2015.

[3] 周明明.基于专家系统和蒙特卡罗方法的计算机围棋博弈的研究[D].南京航空航天大学，2012.

[4] 曹一鸣.基于蒙特卡罗树搜索的计算机扑克程序[D].北京邮电大学，2014.

[5] 张小川.六子棋博弈的评估函数[J]. 重庆理工大学学报，2010.

[6] 刘明慧.计算机博弈的估值方法研究[D].东北大學，2008.

[7] 刘洋.点格棋博弈中UCT算法的研究与实现[D].安徽大学，2016.

[8] 王帅.一种德州扑克的牌力评估方法[J].计算机工程与科学，2017.

[9] 光洋.爱恩斯坦棋计算抓博弈系统的研究与实现[D].安徽大学，2016.

[10] 张玉琪.基于静态评估的计算机围棋UCT算法改进研究[D]. 南昌航空大学，2015.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。