《基于多熵源的移动终端随机数生成方案》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于多熵源的移动终端随机数生成方案

范文

韩冬磊刘世颖

摘要：随着移动智能设备的普及，给用户的数据、隐私甚至是财产安全带来了前所未有的威胁。给用户提供安全应用服务的核心是密码技术，而随机数作为密码技术的信任根，其安全生成是整个应用服务安全保障的根本。然而由于移动终端的应用环境复杂多变，传统的随机数生成方案在移动终端上无法保证所生成随机数的安全性。基于此，提出了一种在可信执行环境（Trusted Execution Environment，TEE）中利用多熵源的伪随机数生成方案。该方案通过利用SRAM PUF生成带有设备硬件特征的随机数与来自移动终端上传感器采集的物理随机数整合成为伪随机数发生器（Pseudo-Random Number Generator，PRNG）的種子，生成满足安全要求的随机数，从而满足移动终端对于随机数的安全需求。

关键词：随机数生成;可信执行环境;SRAM PUF

中图分类号：TP391.4文献标志码：A文章编号：1008-1739（2021）07-55-5

0引言

根据中国互联网信息中心CNNIC发布的2019中国移动互联网发展状况及其安全报告显示[1]，截止2019年6月，我国手机网民规模达8.47亿，网民使用手机上网的比例高达99.1%。随着移动智能设备的普及，针对智能移动设备的安全威胁也日益增多。以境内网民使用比重最大的Android系统为例，由于Android系统的开源性，Android应用市场存在很多恶意应用，这些恶意应用在移动终端后台进行发短信、屏蔽短信、联网扣费及修改上网接入点等恶意操作，不仅会泄露用户个人隐私，还会给用户带来重大经济损失，保障用户的应用安全成为亟待解决的问题。给用户提供安全的应用服务的核心是密码技术，而随机数作为密码技术的信任根，生成的方法是整个应用服务安全保障的根本。

当下移动终端的随机数生成方案主要有2种：第1种是使用软件方法去产生伪随机数，其伪随机源就无法达到足够的安全要求;第2种随机数生成方案是基于移动终端上的传感器采集的真随机数据来产生随机数。这种方法生成的随机数来自物理真随机源，但是因为移动终端上的传感器和采集装置都极有可能被敌手掌控，通过它们采集到的数据可能受到敌手的干扰和篡改，甚至完全暴露给攻击者，所以这种利用单一物理随机源来产生随机数的方案也无法保证足够的安全。除此之外，由于移动终端功能的多样性，上述应用往往鱼龙混杂、应用环境复杂多变，无法保证所生成随机数的安全性。

鉴于以上在移动终端生成随机数的问题，提出了TEE[2]中实现多熵源的随机数生成方案。TEE技术作为硬件隔离技术，能够确保敏感数据在可信环境中得到存储、处理和保护。所以在TEE环境下，能够保证随机数生成与计算安全，大幅度提高了随机数安全性的保障。根据方案，在移动终端上电时系统利用SRAM PUF生成一组随机数，考虑到移动终端上电频率较低以及移动终端SRAM PUF资源较少的情况，还利用移动终端上的物理传感器来采集随机数，然后将这2组随机数进行整合成为伪随机数发生器的种子，生成符合安全要求的随机数。该方案保证了随机数的熵源是来自移动终端SRAM PUF上电初值以及从移动终端的传感器收集的随机数据，解决了利用单熵源生成随机数时带来的安全问题，为移动终端的随机数生成提供了一种新思路。

1核心技术

1.1物理不可克隆函数

物理不可克隆函数（Physically Unclonable Function，PUF）并不是一个数学概念上的函数，是指一个物体（如一个芯片）固有的、不可克隆的、个体所特有的物理特征表现。PUF一般采用挑战-响应的工作方式，每一个PUF实体所具有的这种挑战-响应都是固有的且具有鲜明的个体特征，敌手几乎不可能克隆PUF实体的挑战-响应行为[3]。

PUF因其固有的、唯一的、不可克隆等特性，所以在密钥生成、系统认证等领域有重要的应用。除此之外，PUF的响应会受到噪声影响，绝大多数情况下同一个PUF对于多次同样的挑战所产生的响应并不完全一样。利用这种差异性，在不需要额外硬件成本的情况下，就可以产生安全的高质量随机数。

1.2 SRAM PUF随机特性

SRAM[4]是基于双稳态电路的电子存储技术。每个SRAM单元由6个场效应管MOSFET组成[5]，如图1（a）所示，其逻辑功能可看作是2个交叉耦合的反相器，如图1（c）所示。每个反相器各由1个n-MOS和1个p-MOS组成，剩下2个MOS用于存储状态的读出和写入。从逻辑上看，SRAM单元具有2个稳态可以分别表示‘1和‘0，因此SRAM存储器每个单元在上电时都可以稳定存储一个比特的信息。

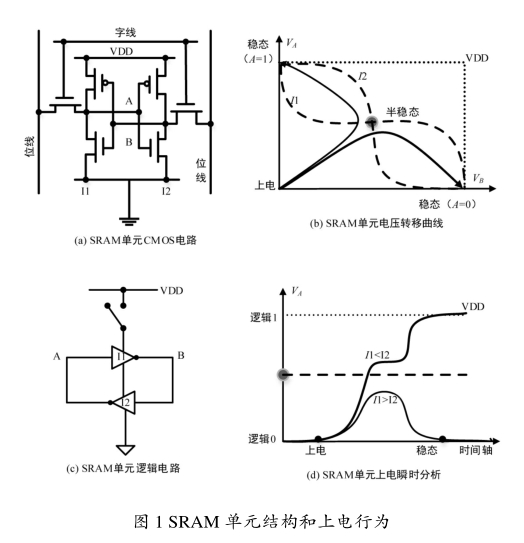
SRAM PUF基于SRAM单元在上电时的瞬时行为，对于SRAM PUF来说，需要读取一段SRAM地址，响应的是对应地址单元格的上电初值。

然而，SRAM单元格上电后无法立刻明确趋向于哪个稳态，而是由2个因素共同决定：首先是制造工艺，其偏差会使2个反相器不完美对称，其中一个反相器会比另一个反相器更强。如果说2个反相器的这种差异比较明显，那么在上电过程中，较强的反相器会很快将SRAM单元的状态推向它所决定的稳态上，在此情况下SRAM单元的上电初值倾向是稳定的。但如果2个反相器的差异并不是很明显，那么此时SRAM单元初值的决定因素就变成了电路噪声。在此情况下，SRAM单元每次上电的初值往往是不一样的，倾向性并不明显，即SRAM单元在每次上电时，会在电路噪声的干扰下随机选择2个反相器中的一个，并推向其对应的稳态，这就是SRAM PUF响应的噪声来源，也是随机性的来源。本文主要利用SRAM上电时受到的电路噪声影响倾向性不明显的特性来提取随机数。

1.3利用物理随机源生成随机数

移动终端可以利用音频采集装置、传感器等多种真随机源来产生随机数。这种提取随机数的方法主要利用移动终端上的器件所记录的数据具有一定的物理随机性，将数据经过适当处理后作为随机数使用，可以作为随机源提取的器件包括加速度传感器、磁力传感器和声音采集装置。

移动终端在通过采集移动终端的加速度传感器、磁力传感器和声音采集装置获得样本数据后，将采集的样本数据使用Hash函数作为熵累加器，不断地将处理后的结果追加到数据池中。随着数据采集地不断进行，数据池的总熵值也会不断增加，当总熵值大于需要产生随机数的位数时，再利用Hash函数计算数据池中数据的消息摘要作为随机数进行输出。

2方案设计与实现

利用SRAM PUF的随机特性以及移动终端上的物理随机源，提出了在TEE中利用多熵源的伪随机数生成方案，具体方案设计如下。

移动终端每次系统上电启动时，在TEE下利用SRAM PUF的噪声特性提取一部分随机数。考虑到现在对移动智能终端的使用习惯，关闭移动终端或者重新启动移动终端的频率变得越来越小。此外，由于制造过程中的不可控因素，会造成SRAM逻辑单元上电初值大部分会趋向于一个稳定的状态，而受到电路噪声影响的符合SRAM PUF随机特性的单元比重较小。鉴于这两方面的局限性，从TEE中获取的随机数很难满足移动终端中大量随机数的使用需求。

为了解决这个问题，除了利用SRAM PUF的噪声特性提取随机数之外，还利用移动终端的物理传感器采集数据获取来自外界的随机序列。将这2组随机数进行异或操作，产生一个定长的随机数，最终用这个随机数作为PRNG伪随机数发生器的种子来产生大量随机数。

2.1 SRAM PUF随机数提取

2.1.1 SRAM生成随机数最小熵分析

在信息论中，熵表示对某件事的不确定性度量，熵值越大表示随机性越大，可以得到的信息量越少;反之熵值越小表示随机性越小，可以得到的信息量越多。为了获得高质量的真随机数，需要获得高熵值、独立且均匀分布的随机数序列。对于利用SRAM PUF上电-激励响应来产生的序列，分析了其最小熵[6]，并证明了利用Hash函数的特性可以从熵值较低的低质量随机数中提取定长的熵值较高的高质量随机数。

此外，为了获得好的随机提取性能，每次提取时使用的通用Hash函数族的索引下标应该是随机选取的，而目的就是为了提取随机数，这也使得信息理论上安全的随机提取器无法满足实际要求的关键问题。

鉴于信息理论上安全的随机提取器问题，不妨借鉴某些基于物理随机种子的伪随机数发生器（Pseudo-Random Number Generators，PRNG）结构。这些PRNG从物理源中提取熵，通过基于香农熵估计的随机性累计，将一定的熵累积在定长序列中。这种结构的设计准则和实践技术在Barker和Kelsey、Eastlake等人，以及Kelsey等人关于随机数发生器的著作中均有讨论。在提出的结构中，都利用安全Hash函数作为所谓的熵累加器。所以可以利用一个Hash函数作为熵累加器，来从熵值较低的低质量随机数中提取定长的熵值较高的高质量随机数，在利用SRAM提取随机数的方法中，采用SM3密码杂凑算法[7]作为熵累加器。

2.1.2利用SRAM PUF提取随机数方法

利用SRAM PUF的噪声特性产生真随机数，但是由于直接读取的上电初值的熵值不够，所以利用Hash函数可以作为熵累加器的特性，通过读取的低熵值随机序列来提出将近满熵的高质量真随机数。随机数提取方法要有3个阶段：

①移动智能终端启动时，在TEE中读取一段SRAM单元的上电初值。

②在TEE中将提取的响应对进行Hash来产生定长的将近满熵的高质量随机数。

③通过上述过程产生一个高质量随机数。

按照上述方案，可以仅需要提取一个256 bit接近满熵的随机数。首先在移动智能终端的TEE中选择4 KB数据提取初始上电激励响应对，将此作为随机提取器的输入;然后采用SM3密码杂凑算法，将平均熵值较低的低质量随机序列，转换为均匀分布长度为256 bit的高质量随机数，完成利用SRAM PUF提取随机数的工作。

2.1.3 SRAM提取随机数测试结果

由于在移动终端直接读取CPU上高速缓存中上电初值的技术难度太大，所以使用Zynq-7000 AP SoC开发板来模拟对SRAM上电初值的采集过程[8]。通过开发板上的扩展卡槽将一块类型为IS61LV6416-10TL的芯片与开发板相连，然后采集芯片上的SRAM上电初值数据。

利用以上方法在SRAM芯片上选取4 Kbit数据，循环上电100次，统计上电激励响应对，利用公式（1）～（2）分析并计算4 Kbit的最小熵，结果为5.46%，所以该SRAM芯片的最小熵比率约为5.4%。保守的認为该SRAM芯片的最小熵为2%，所以如果在系统上电的过程中，利用提取CPU高速缓存中的初值来产生256 bit随机数，则至少需要读取长度为256/0.02=1.6 Kbit的Cache上电初值，所以读取长度为4 Kbit的上电初值来提取265 bit的随机数绰绰有余。

2.2物理随机源真随机数提取

2.2.1利用物理随机源提取随机数方法

利用移动终端上的一些器件所记录的数据具有一定的物理随机性，将数据经过适当处理后，可以作为随机数使用的特性来提取随机数。移动终端上可以作为随机源提取的器件包括：加速度传感器、磁力传感器和声音采集装置。通过读取来自这些物理随机源的数据作为生成随机数的熵源，与基于SRAM PUF提取随机数时遇到的问题一样，读取来自物理随机源的原始数据熵值是不够的，所以同样需要利用Hash函数可以作为熵累加器的特性，通过读取低熵值的随机序列来提出将近满熵的高质量真随机数。随机数提取方法要有3个阶段：

①通过采集移动终端的加速度传感器、磁力传感器和声音采集装置获得样本数据。

②将不断从物理随机源中采集到的样本数据通过SM3密码杂凑算法计算后追加到数据池中。

③随着数据采集的不断进行，数据池的总熵值会不断增加，当总熵值大于需要产生随机数的位数时，利用SM3密码杂凑算法计算后输出随机数。

接下来需要对从物理随机源中提取的随机数进行熵值评估，来确定需要从各种传感器中读取多长的数据才可以达到提取定长随机数的目的。

2.2.2物理随机源随机数联合熵评估

從产生速率来看，声音采集装置每秒钟可提供的熵至少为8 000×1.999=15 992 bit，加速度和磁力传感器（一个轴）平均每秒可提供的熵分别为92.95 bit和41.8 bit，所以通过这些传感器足够满足在物理随机源中获取随机数的需求。

3结束语

移动智能设备的普及使得针对移动智能设备的安全威胁也日益增多，如何有效地保障用户隐私和应用安全是一个关键且迫切的问题。而随机数作为信息安全系统的核心，其安全性不容忽视。本文首先分析了移动终端上随机数提取技术的现状以及面临的问题，并针对这些问题提出了一个在移动终端基于多熵源的随机数生成方案，该方案通过利用SRAM PUF生成的带有设备硬件特征的随机数与来自移动终端上传感器采集的物理随机数进行异或整合成为伪随机数发生器的种子，生成满足安全要求的随机数，使得生成的随机数符合了安全标准，满足了移动智能设备系统对于随机数的安全需求。

参考文献

[1]于朝晖.CNNIC发布第44次《中国互联网络发展状况统计报告》[J].网信军民融合，2019（9）：30-31.

[2]范冠男，董攀.基于TrustZone的可信执行环境构建技术研究[J].信息网络安全，2016（3）：21-27.

[3]张紫楠.物理不可克隆函数的研究与应用[D].郑州：解放军信息工程大学，2013.

[4]刘客.嵌入式SoC片上SRAM PUF的设计与实现[D].武汉：华中科技大学，2013.

[5] ROEL M.Physically Unclonable Functions： Constructions， Properties and Applications [M].Berlin：Springer，2013.

[6] HERREWEGE A V，LEEST V V D，SCHALLER A， et al. Secure PRNG Seeding on Commercial Off-the-shelf Microcontrollers[C]//Proceedings of the 3rd International Workshop on Trustworthy Embedded Devices.Berlin：ACM， 2013：55-64.

[7]申延召.SM3密码杂凑算法分析Diss[D].上海：东华大学， 2013.

[8] ZHAO Shijun，ZHANG Qianying，HU Guangyao，et al. Providing Root of Trust for ARM Trustzone using On-Chip SRAM[C]// International Workshop on Trustworthy Embedded Devices，Scottsdale：ACM，2014：25-36.

[9] HONORIO M，PEDRO M H，PEDRO P L，et al. On the Entropy of Oscillator-based True Random Number Generators Under Ionizing Radiation[J]. Entropy，2018，20（7）： 165-180.

[10]齐玮，王仁明，李夕海，等.连续型随机向量联合熵的离散方差分离估计[J].数学的实践与认识，2010，40（13）：102-109.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。