网站首页  词典首页

标题	腔体滤波器温度补偿和温度试验
范文	冯文文++李磊++王惠生 摘 要： 为了减小腔体滤波器随温度变化对性能的影响，利用CST仿真软件对腔体滤波器进行温度分析，并结合ADS软件对该滤波器进行模拟，得出60 ℃温差下的幅相变化数据和频漂数据。设计了一个采用双导体结构的滤波器，该滤波器盒体为铝合金材料，谐振杆和调谐螺钉为殷钢。通过分析温度试验中误差的影响因素，提出一种较小误差的温度试验方法，并对调试好的滤波器进行温度试验，试验结果显示该滤波器的频漂为5.6 ppm/℃，试验数据跟仿真结果吻合。 关键词： 腔体滤波器； 温度补偿； 殷钢谐振器； 温度试验 中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）10?0131?03 0 引 言 微波滤波器广泛应用于各种通信系统中。通常情况下，微波滤波器要在较宽的温度范围内工作，当环境温度发生变化时，滤波器由于谐振腔的热胀冷缩，其谐振频率会产生变化，由此可能导致滤波器驻波比变大，损耗增加，相位出现偏移等情况，也就是常说的温度漂移现象。如果温度漂移引起的幅相变化超过某一数值，将会影响信号的传输质量。因此对微波滤波器进行温度补偿非常必要。滤波器温度补偿的方法有很多种，文献[1]通过一个可以随温度自动调整的谐振杆，来保证谐振杆跟腔体之间的电容不变，以进行温度补偿；文献[2]使用形状记忆合金制作的弹簧装置进行温度补偿；文献[3?4]利用介质材料与金属材料相反的热膨胀系数对谐振腔进行温度补偿；文献[5]选用不同温度系数的材料，使材料温度变化对谐振频率的影响相互抵消。 综合考虑加工、成本、可靠性等因素，本文利用CST仿真软件，采用双导体结构，优化谐振腔各部分的尺寸参数[6]，设计了一个外腔体用铝材，谐振杆用殷钢的滤波器，并利用ADS仿真软件计算出窄带滤波器的温度特性。同时，本文将温度试验方法进行了改进，减小了试验误差。滤波器温度试验结果表明该滤波器的温度漂移特性跟仿真结果吻合。 1 温度补偿设计方法 1.1 谐振腔模型 在CST仿真软件中，建立滤波器谐振器的三维模型，假定谐振器各尺寸都是按照热胀系数线性膨胀，由于谐振器的形变量极小，为了保证计算精度，设置较宽的温度范围，CST中谐振腔模型如图1所示。将殷钢的热胀系数1.3 ppm/℃和铝合金材料的热膨胀系数24 ppm/℃，代入谐振器模型，分别计算腔体和内导体为铝材、腔体为铝材内导体为殷钢、腔体和内导体都是殷钢，这三种情况下谐振器的频率变化如图2所示。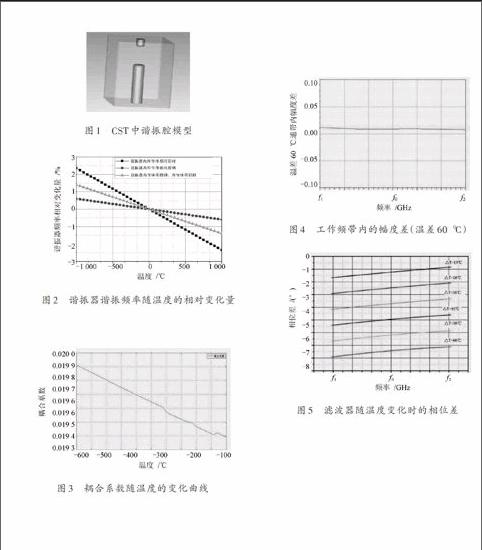 图1 CST中谐振腔模型 图2 谐振器谐振频率随温度的相对变化量 由图2可知，如果腔体和内导体都用铝材的谐振频率变化量为25 ppm/℃，腔体和内导体都用殷钢的谐振频率变化量为1.5 ppm/℃，腔体用铝材内导体用殷钢的谐振频率变化量为5 ppm/℃。可以看出谐振器用铝材内导体用殷钢的谐振器可以起到很好的温度特性。 1.2 耦合系数变化模型 按照铝材的温度膨胀系数计算双腔谐振器的奇偶模频率，利用公式：[k=f22-f12f22+f12]，可得出谐振腔随温变化时耦合系数的变化曲线，如图3所示，耦合系数的变化量很小，即使全铝材的谐振腔，耦合系数的变化量都小于1 ppm/℃。 图3 耦合系数随温度的变化曲线 1.3 ADS中温度变化仿真结果 将谐振器的频率变化情况和耦合系数变化情况代入ADS滤波器模型，可以得出滤波器在温度变化时的幅相变化曲线。由于滤波器幅度变化很小，仅给出温差60 ℃的曲线，如图4所示。 从图5可以看出，该滤波器在温差60 ℃时幅度变化量约为0.05 dB，相位变化约8°，通过数据拟合可以计算出滤波器的频漂约为6.3 ppm/℃。 图4 工作频带内的幅度差（温差60 ℃） 图5 滤波器随温度变化时的相位差 2 温度试验 试验是验证设计结果的重要环节，由于滤波器随温度变化引起的幅相变化量较小，在进行环境试验时必须考虑误差的影响。试验过程中产生的误差主要是由测试系统误差和计算精度误差等误差项引起的，其中测试系统误差包括：矢量网络分析仪的测量精度，高低温箱的控温精度和温箱内温度的均匀程度等方面。其中最主要的试验误差是测试电缆组件引起的试验误差，为了减小测试电缆组件引起的幅相误差，在温度试验前应先将测试电缆组件的随温度特性记录下来，然后在保证温度箱中的电缆长度和形状不变的情况下，再接入待测滤波器进行温度试验。同时矢量网络分析仪设置更多的测试频率点，尽量缩短温箱内测试电缆的长度，温箱温度到达某一温度时要保温半个小时以上，通过以上方法尽量减小测试系统的误差。 3 数据处理结果 将温度试验中的测试数据进行处理后可以得出幅相数据如表1所示，滤波器在-30～60 ℃的范围的幅相变化曲线如图6和图7所示，其相位变化（以15 ℃时的相位归零）在整个温度范围内小于8.7°，幅度变化小于0.17 dB，利用数据拟合求得该滤波器的频率漂移为5.6 ppm/℃，跟ADS仿真数据吻合很好。 表1 滤波器温度试验数据 图6 滤波器温度试验时相位变化曲线 4 结 语 窄带滤波器在设计过程中不仅要关注技术指标的实现，还应当关注温度对技术指标的影响。本文提供的方法可以帮助此类滤波器进行温度影响的仿真分析，避免因选材不当造成滤波器失效。 图7 滤波器温度试验时幅度曲线 参考文献 [1] COGDELL J R， DEAM A P， STRAITION A W. Temperature compensation of coaxial cavities [J]. IRE Transactions on Microwave Theory and Techniques， 1960 （3）： 151?155. [2] KEATS B F， GORBET R B， MANSOUR R R. Designed and testing of SMA temperature?compensated cavity resonators [J]. IEEE Transactions on Microwave Theory and Techniques， 2003， 51（12）： 2284?2289. [3] LIM Sang?Kyn， LEE Han?Young， KIM Jun?Chul， et al. The design of a temperature?stable stepped?impedance resonator using composite ceramic materials [J]. IEEE Microwave and Guided Wave Letters， 1999， 9（4）： 143?144. [4] 柳光福，刘启明.介质加载谐振腔滤波器的频率温度系数设计[J].航空电子技术，2007，38（3）：42?46. [5] 李军，贾宝富.双金属谐振腔温补方法研究[J].真空电子技术，2009（1）：61?66. [6] 任菁圃，张德伟，牛忠霞，等.一种同轴谐振腔的温度特性研究[J].信息工程大学学报，2005（4）：31?33.
随便看	探究日本文化内涵及日语学习策略 探究中国近现代艺术歌曲在高校声乐教学中的应用 心理健康教育在高校学生管理中的思考 辽东学院校园垃圾分类观念和现状调查 浅析课程思政如何融入应用型课程教学 翻转课堂模式在高职声乐教学中的应用 高职院校艺术类课程信息化教育教学改革研究 高职院校学生职业素质教育的改革研究 高职人物形象设计专业“实用型”人才培养 课程思政在思想政治教育工作中的价值分析 试论大学生法治素养培育措施 职业中学英语教学之我见 立德树人视域下加强体育专业学风建设研究 电气自动化技术专业卓越技术技能人才培养初探 浅谈儿歌即兴弹唱的一般步骤 浅析三维动画教学中的关键帧制作 探究高考英语改革背景下高中英语教学的开展 思政教育在影视课改中的作用 广播电视编导专业人才培养现状、存在问题及对策 大学英语考级对学风建设的影响及路径研究 大学生思想政治素质教育中美育的运用 多媒体信息技术助力室内设计教学的发展研究 基于文博信息技术下的创新体系研究 关于职业学校信息技术教学改革问题 中职计算机专业课程课堂教学探究与策略 erupted eruptible erupting eruption eruptively erupts erythrocyte erythrocytes erythrocytic esc escalate escalated escalates escalating escalation escalationclause escalation clause escalations escalator escalator clause escalatorclause escalators escalatory escapade escapades 羊裘之徒 羊裘垂钓 羊裘老子 羊裘钓 羊裘钓泽 羊裙 羊角 羊角大灯 羊角手罩 羊角插在篱笆里——伸头容易回头难 羊角树 羊角疯 羊角葱 羊角葱靠南墙——越发老辣 羊角辫 羊角风 羊触藩篱 羊触藩篱——进退两难 羊负来 羊质虎形 羊质虎皮 羊贪狼很 羊贪狼狠 羊走人汤， 自送其死。 羊走入汤——自送其死

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。