网站首页  词典首页

请输入您要查询的论文：

　

标题 基于属性权重的Bagging回归算法研究
范文 孟小燕



摘 要： 提出一种新的回归算法——基于属性权重的Bagging回归算法。首先使用支持向量机回归或主成分分析方法对样本数据的属性赋以一定的权值，以表明该属性在回归过程中的贡献大小；再根据不同属性的权重大小构建训练使用的多个属性子集。在构建这些属性子集的过程中，按照不同属性权重在总权重中所占比重为概率进行，使得对回归贡献大的属性有更大的可能被选入属性子集当中参与训练；最后，对这些属性子集进行训练，生成相应的多个回归子模型，这些子模型的集合就是通过基于属性权重的Bagging回归算法训练得到的最终模型。
关键词： 支持向量机； 属性权重； 集成学习； 主成份分析； 回归算法
中图分类号： TN911?34； TM417 文献标识码： A 文章编号： 1004?373X（2017）01?0095?04
Abstract： An attribute weight based new regression algorithm called Bagging regression algorithm is proposed. The support vector regression or principal component analysis is used to value a certain weight for the sample data to show the attribute contribution in the regression process. And then the multiple attribute subsets for training were constructed according to the weights of different attributes. The constructing process of the attribute subsets is conducted in accordance with the weights of different attributes as a percentage of the total weight to determine the probability， which makes the attribute with great regression contribution possibly be selected in the attribute subsets for training. The attribute subsets are trained to generate the corresponding multiple regression sub?models. The assembly of these sub?models is the final model trained by the Bagging regression algorithm based on attribute weight.
Keywords： support vector machine； attribute weight； ensemble learning； principal component analysis； regression algorithm
在诸多回归方法中，线性回归方法是一种比较传统的回归方法，通过对自变量和应变量之间统计量的分析，得到一个线性函数[1]。這种回归方法能够很好地拟合线性关系的数据，但是，对于非线性关系的数据则无法做到好的拟合。为了应对线性回归方法的缺陷，提出了支持向量机回归方法。支持向量机回归方法能够解决许多非线性回归问题[2]。本文通过综合应用支持向量机回归方法、属性权重方法和集成学习方法，取长补短，提升现有的支持向量机回归方法的准确度[3]。
1 基于属性权重的Bagging回归方法
1.1 计算属性的权重
1.1.1 通过SVM方法计算属性权重
1.2 基于属性权重对属性进行选取
对于样本数据属性的取舍是基于属性的权重来决定的。如果一个属性的权重比较大，那么认为这个属性对于最终的模型训练具有比较大的贡献，应当让它有比较大的概率被保留[4]。而一个属性的权重比较小，那么就认为这个属性对于最后的结果贡献不大，保留它的概率就比较小了，换句话说，保留这个属性的可能性就比较低。
对于属性保留与否的概率判断，并不是通过权重感性的决定，而是通过权重值进行理性的分析后才能做出合理的决定。此处，采用的是不同属性的权重在总权重值中所占比来确定保留这个属性的概率的，即对于属性它被赋值的权重为，是否保留这个属性的概率为。
1.3 交叉验证确定属性子集大小
1.3.1 Holdout验证
Holdout验证方法首先是从原始的样本中随机选择一部分数据作为验证集，剩下的样本则作为训练集[5]。之后使用一种需要验证的机器学习方法，利用训练集训练得到一个模型，最后用验证集对这个模型进行验证，得到这个模型性能的结果。
1.3.2 折交叉验证
折交叉验证的做法是首先将原始的样本集划分为份。从其中选择一个样本子集作为验证集使用，而剩下的个样本子集则合起来作为一个训练集。接下来，使用需要验证的机器学习方法对训练集进行训练并得到模型，最后，使用这个模型对验证集进行验证，得到结果。之后重新选择一个新的样本子集（j≠i）作为新的验证集使用，并使用剩下的个样本子集作为训练集[6]。使用同样的方法能够得到新的验证结果。如此重复，直至所有的样本子集都被选作验证集使用过一次，得到了验证结果集。对于这个机器学习算法效果的判断就是对个验证结果的平均，或者使用这个验证结果集与别的数学方法进行结合。
1.3.3 留一验证
留一验证实际上是折交叉验证的一个特例。假设原始样本集中具有个样本，那么，所谓的留一验证就是折交叉验证。首先需要从原始样本集中选择一个样本作为验证，剩余的所有样本作为训练集使用，如此重复，直到所有的样本都被用作验证一次，并将验证的结果平均，得到机器学习方法的性能结果。
1.4 Bagging方法训练回归模型
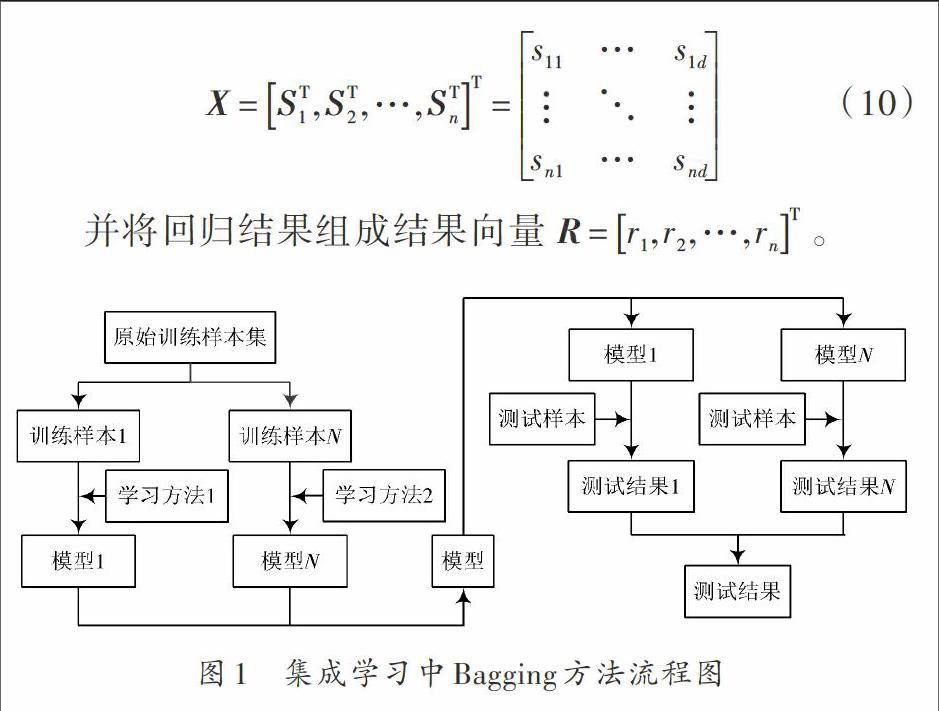
对于回归模型的训练，采用集成学习Bagging方法，其流程图如图1所示。Bagging方法需要对不同的子模型进行训练后形成一个模型集[7]。测试时，根据这个模型集中不同子模型的测试结果，综合给出整个模型的最终结果。
1.5 基于属性权重的Bagging回归方法
1.5.1 A基于SVM的属性权重赋值方法
（1） 将统计得到的原始样本数据集组成样本列矩阵
（2） 使用SVM回归方法对数据进行预处理，得到回归直线的切向量信息，并对数据第个属性赋权重值为。
（3） 以为第个属性的概率对样本数据的属性进行无放回的抽取，组成新的属性子集。属性子集的大小从1开始直至完全选择所有的属性进入属性子集。对于每一个不同大小的属性子集，需要构建适当数量的属性子集，并对训练集进行交叉验证[8]。验证时，对每个属性子集经过训练后得到的模型测试结果进行平均，取得最终的验证结果。通过交叉验证确定性能最优的属性子集大小。
（4） 依照上一步的方法，结合概率无放回地抽取样本数据的属性，组成属性子集，直至属性子集大小为最优。反复这个步骤，直到有了足够多的属性子集可用作集成学习。使用支持向量机回归方法对每一个属性子集进行训练得到回归模型。保留所有的回归模型和相对应的属性信息，得到最终的回归器。
（5） 测试时，测试样本需要经过每一个回归模型的检验。测试样本保留在回归模型中保存的属性信息所包含的属性，组成一个属性子集，将属性子集送入回归模型进行测试，得到单个回归模型的回归结果。反复以上步骤，直至所有的回归模型都对样本进行了测试，得到了结果。对这些结果求平均值，便是利用SVM确定权重，是基于属性权重的Bagging回归方法的最终回归结果。
1.5.2 基于PCA的属性权重赋值方法
（1） 将统计得到的原始样本数据集组成样本列矩阵
对这个协方差矩阵求解特征值和特征向量，得到相应的特征向量矩阵和特征值向量，与是一对相对应的特征向量和特征值。对数据第个属性赋权重值为。
（3） 以为第个属性的概率对特征向量矩阵进行无放回的选择，被选择的矩阵向量加入到属性变换矩阵中。属性变换矩阵的列数从1开始直至完全选择所有的特征向量进入属性变换矩阵。对于每一个不同的属性变换矩阵列数，需要构建适当数量的属性变换矩阵，使用属性变换矩阵对原数据矩阵进行变换，得到新的属性子集，并对训练集进行交叉验证。验证时，每个属性子集经过训练后对得到的模型测试结果进行平均，取得最终的验证结果。通过验证确定性能最优的属性子集大小，即属性变换矩阵的列数。
（4） 依照上一步的方法，结合概率无放回地选择特征向量加入属性变换矩阵当中去，组成属性变换矩阵，直至属性变换矩阵的列数达到最优。使用属性变换矩阵对原数据矩阵进行变换，得到属性子集。重复这个过程，指导足够多的属性子集用作集成学习。使用支持向量机回归方法对每个属性子集进行训练，得到回归模型。保留回归模型和相对应的属性变换矩阵，得到最终回归器。
（5） 测试时，测试样本需要经过每一个回归模型的检验。测试样本经过属性回归矩阵的变换得到一个属性子集，将属性子集送入回归模型进行测试，得到单个回归模型的回归结果。反复以上步骤，直至所有的回归模型都对样本进行了测试，得到了结果。对这些结果求平均值，便是利用PCA确定权重，是基于属性权重的Bagging回归方法的最终回归结果。
2 实验平台和数据
2.1 试验过程
此次实验使用“housing_scale”和“eunite2001”两个样本数据集进行。“housing_scale”样本集已经过归一化处理，但未区分训练集和测试集。因此，在对这个样本集进行实验时，就需要从中选择一部分数据作为测试集使用。在实验前，需要先做归一化处理，这两个样本数据集的概况如表1所示。
2.1.1 确定属性权重
属性权重赋值的方法有两种：一是需要对样本数据进行预处理的支持向量机方法；二是根据样本数据统计学特性进行赋值的主成分分析方法。使用支持向量机方法得到的housing_scale，eunite2001样本集中各个属性的权重如图2，图3所示。
从图2中可以看出，housing_scale样本集数据的各个属性中，具有最高权重的三个属性权重被选择的概率和为42.97%，相对应地，权重最低的三个属性被选中的概率和仅为9.01%。仅从概率上来说，具有最高权重的三个属性被选择的可能性是最低权重的三个属性的5倍，形成了鲜明对比。
eunite2001样本数据集的各个属性的权重差异更为明显，最高的三个权重被选择的概率和为37.33%，而最低的三个被选择的概率则仅为0.256 5%，相差高达145倍之多。这表示在进行属性子集构建的过程中，权重最低的那些属性几乎没有可能被抽取。
使用主成分分析方法得到的housing_scale样本最终确定的权重值在各个属性之间的差异巨大，权重最大的属性占到权重总和的61.27%，换句话说，在构建属性子集的过程中，有超过一半的可能性会将这个属性选择在内。
eunite2001样本虽不像housing_scale屬性权重之间有非常大的差异，但它的差异也决不能轻视。被选择概率超过10%的属性仅存在5个，而剩余的11个属性需要共享剩余16.29%的概率，这就会导致最终在属性子集构建的过程中不同的属性被选入的可能性大不相同。
2.1.2 对最佳属性子集的实验
在进行实验的过程中，除了之前提到的支持向量机属性权重赋值方法和主成份分析属性权重赋值方法外，还将对随机属性权重赋值方法进行实验。实验将使用10折交叉验证进行，让属性子集的大小从1开始逐步增长，直至所有的属性都被选入属性子集中。对于每一个属性子集的大小进行50次交叉验证，对这50次验证的结果求平均得到最终的性能评价。其中，性能最优的属性子集大小即为需要的结果。
通过实验可以看出，随着属性子集大小的增加，模型的性能也得到了不断的提升。但当模型的性能提升到最优点后，模型的性能便开始下降，直至属性子集为样本属性全集。随着属性子集的大小接近样本属性的总数，回归结果的方差变得越来越小，即稳定性增强了。因此，不同次实验间的差异性也就减小了。
2.1.3 通过集成学习训练回归模型
采用最优的属性子集大小来构建子模型的训练集，并对1～100个子模型的数量进行回归性能的实验。每一个子模型数量需要进行50次实验并求取平均和方差。通过实验数据可以发现，当Bagging方法集成的子模型数量较少时，回归模型的准确度不高，但随着参与到Bagging方法中的子模型数量的增长，整个回归模型的准确度迅速提升。但回归模型的性能并不会发生太大的变化。
2.2 实验分析
在这次实验中，通过对housing_scale和eunite2001两个样本集使用基于属性权重的Bagging回归算法，统计在不同属性子集大小和不同集成规模情况下的实验数据，分析通过支持向量机方法确定属性权重方法和主成分分析方法确定属性权重方法之间的差异。
对属性的权重进行赋值，使其能够按照不同的概率被选入属性子集中，这使得权重高的属性即对回归结果贡献大的属性，在训练时能够得到更多的训练。而权重低的属性，虽无法得到与高权重属性相同的训练机会，但在训练时并未被忽略，这一点是通过集成学习得到的保证。这样的操作使得回归模型在训练时更关注主要信息，兼顾次要信息，提升模型的性能。
3 结 论
支持向量机方法自从被提出以来，已经在许多领域得到了广泛的应用，并得到了不少的好评与支持。因此，本文选择支持向量机方法进行回归。基于属性权重的属性子集的构建对于最终回归结果的影响，通过使用权重来区别不同重要性的属性有实验依据。高权重的属性比低权重的属性更能反映样本的性质，有目的的选择高权重的属性参与训练的回归方法比随机选择属性参与训练的回归方法在准确度上能够提升10%的性能。
通过实验，集成学习方法中的Bagging方法的重要性也得到了体现。在实验中使用Bagging方法，消除了样本中噪声对最终回归的影响，使得最终的回归结果在提升准确度的同时，保证了稳定性。最重要的是，使用Bagging方法能够让低权重的属性不被忽略，同样能够参与到模型的训练中，使模型能够更好地反应样本的真实情况。
参考文献
[1] 杜树新，吴铁军.用于回归估计的支持向量机方法[J].系统仿真学报，2003，15（11）：1580?1585.
[2] 姚明海，赵连朋，刘维学.基于特征选择的Bagging分类算法研究[J].计算机技术与发展，2014（4）：103?106.
[3] TAX D M J， DUIN R P W. Support vector domain description [J]. Pattern recognition letters， 1999， 20（11）： 1191?1199.
[4] 谷雨，郑锦辉，戴明伟，等.基于Bagging支持向量机集成的入侵检测研究[J].微电子学与计算机，2005，22（5）：17?19.
[5] 华德宏，刘刚，兰家隆.一种改进的一元线性回归算法[J].现代电子技术，2006，29（7）：63?65.
[6] 于玲，吴铁军.集成学习：Boosting算法综述[J].模式识别与人工智能，2004，17（1）：52?59.
[7] 张春霞，张讲社.选择性集成学习算法综述[J].计算机学报，2011，34（8）：1399?1410.
[8] 丁里，毛力，王晓锋.应用于p2p流分类的一种改进Bagging学习算法[J].软件导刊，2014（5）：71?73.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 1:52:38