《“有方向了吗”》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

“有方向了吗”

范文

黄雪芬

“教育，即经验连续不断地改造.”（杜威）认知心理学也认为小学生学习数学的过程是新旧知识不断同化、顺应、调查、扩充并形成新的认知结构的建构过程，因而，学生原有的知识、经验对学生学习新知有着重要的作用.教学中如何运用转化的数学思想方法帮助学生搭建新旧知识间的桥梁，沟通联系，积累数学活动经验呢？下面以苏教版三年级下册“两位数乘两位数”的教学片段为例，谈谈转化思想在教学中的应用与渗透.

“数学的特点之一是它具有很强的抽象性，随着学习的不断深入，数学问题的抽象性也不断加强.”计算教学的问题则在算理的理解上，如果能把抽象的算理问题转化为操作或直观的问题，那么，不但使算理容易理解，而且经过不断的“抽象—直观—抽象”的训练，学生的思维能力也会逐步提高.

以下是教学片断，在学习本课内容之前，学生已经理解了乘法的意义，掌握了多位数乘一位数的笔算及两位数乘一位数、整十数、整百数的口算乘法.

（课件展示由一個点动态演变成一行14个，共2行的点子图）

师：一行14个，2行一共有多少个？怎么列式？

生：14×2.

师：这是两位数乘一位数的乘法.跟老师连续拍4次手，看看点子会怎样？

（学生一起拍手，点子随之增加，从2行扩展成4行、8行、10行、12行）

师：现在一共有多少个，怎么列式？

生：14×12.

师：变成了两位数乘两位数的乘法.想想，这只是一个乘法算式吗？我可看到了很多数学知识.谁来说说？

（学生编题）

师：我也说一个，屏幕出示：每套书14本，买12套，一共多少本？估算一下，大约是多少？

生：把14看作15，12看作10，大约就是150本.

生：把12估成10，大约是140本.

师：公布正确答案.答案就是——出示点子图结果，每行14个，12行.

师：看到书了吗？

生：每个点子就代表一本书.

师：拿出学习纸，上面有点子图.可以数一数，也可以拿出红色笔，在点子图上圈一圈、画一画，还可以算一算.

（学生独立尝试解决）

反馈算法.

① 14×2=28，② 14×6=84，③ 14×10=140，

28×6=168；84+84=168；14×2=28，

140+28=168.

……

师：现在告诉老师，14×12等于多少？说说刚才都是怎么做的？

（交流想法）

师：看出来了，14×12不会算，可分成14×2会算，14×6会算，14×10也会算.

师：是的，把不会的知识变成会的知识来解决，是一种很好的学习方法.现在一个个数的同学有方向了吗？

经历这样的学习过程，一句“有方向吗”虽是这部分教学短暂的结点，也给后续的解决问题指明了方向，潜移默化之中渗透学习方法的指导，数学转化思想的培植及有效学习经验的积累.

研读片断中“转化”的运用.

从“这只是一个乘法算式吗？我可看到了很多数学知识”，打开了数学与学生生活实际的联系之门.带领学生把数学知识带回现实生活，去生活中找原型，将一道普通的计算习题转化为解决生活中常见的实际问题，沟通生活经验与新知的联系.让学生感受到数学与生活如此之近，数学源于生活、取之于生活，终将回归生活.通过转化培养学生发现问题、提出问题的能力，发展应用意识与创新意识.

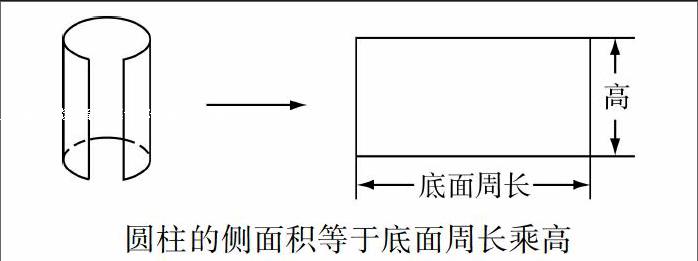
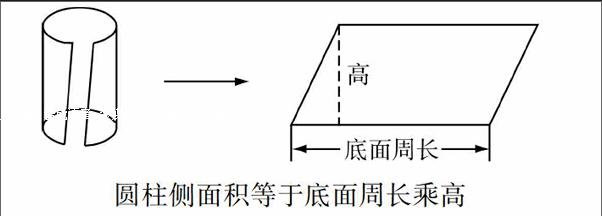
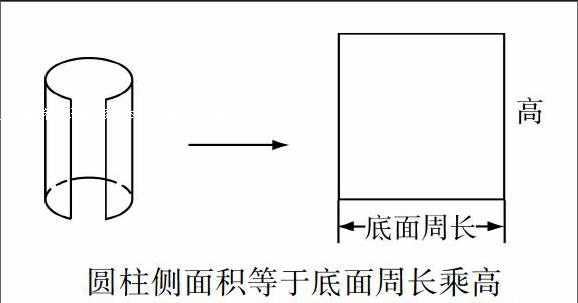
在估算完14×12的积大约是多少后，教师“公布正确答案”，本以为正确答案无非就是出示积等于168，没想到授课教师却以点子图作为替代.在学生疑惑的目光中，问道：“看到书了吗？”学生恍然大悟，明白一个点子就代表一本书，将“数”巧妙转化成“形”，为后续学习、思维发展找到形象化的载体.三年级学生的思维处于从具体到抽象的过渡阶段，学习数学时同样需要有直观表象作为支撑，教师借助点子图的“意外”出现，将抽象的数学问题转化为直观的可操作的问题，帮助学生利用点子图进行描述、分析，使复杂的数学问题变得简明形象.

“可以数一数，也可以拿出红色笔，在点子图上圈一圈、画一画，还可以算一算.”通过动手操作唤醒已有的知识经验，将两位数乘两位数的乘法问题转化为两位数与一位数、与整十数的乘法.学生反馈得出12个14，可以先算2个14是28，再算6个28是168；先求出一半即6个14是84，再84+84=168；12个14先算10个14，再加上2个14，即140+28=168等多种方法.“14×12不会算，可分成14×2会算，14×6会算，14×10会算.是的，把不会的知识变成会的知识来解决，是一种很好的学习方法.”引导学生感受拆分解决的策略，有效植入了数学转化思想.

这样的教学过程，几次运用转化，沟通新旧知识的联系，架设学习的桥梁，学生的学习还会没有“方向”吗？

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。