《高考难点探究》-哲学论文-论文范文参考-科学狗论文网

标题

高考难点探究

范文

傅俊杰

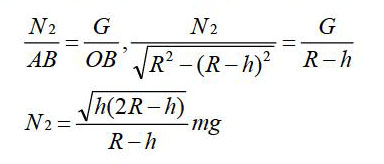
摘要：高中有些知识点就比较难，针对于物理来说有更多的难点和重点。下面对于物理的极值问题的求解进行一些探讨，可以解决一些问题。

关键词：高中物理;物理极值

一、引言

极值问题则是指物理变化过程中，随着条件数量连续渐变越过临界位置时或条件数量连续渐变取边界值（也称端点值）时，会使得某物理量达到最大（或最小）的现象，有关此类物理现象及其发生条件研究的问题称为极值问题[1]。在处理这些问题的时候，我们需要找到已知条件和未知条件的关系，对于极值文题，我们可以用以下几种方式进行处理。

二、二次函数求极值

在物理学习中，遇到的问题是待求物理量随着另外物理量的变化而变化，并且变化形式为：y=ax2+bx+c可以用到这种解题方式。因为y=ax2+bx+c可以转换为y=（ax+m）2+k。

（1）当a>0，不论x取何值，a（x+m）2≥0。则 x=-m 时，y有极小值，即所求的物理量有最小值。Ymin=k=（4ac-b2）/4a。（2）当a<0，不论x取何值a（x+m）3于≤0。则 x = - m 时，y 有极大值，所求物理量就有最大值。Ymin=k=（4ac一b2）/ 4a。

例：例1如图圆环是一一个电阻丝，阻值为R，A点固定，B点可以在圆环滑动。求A、B两点间的最大阻值是多少？

分析：A、B两点把圆分成两部分，两部分并联阻值为A B两点间的电阻。B点无论是在上面，还是在下面成接近A点阻值都越来越小，如果B点与A点重合了，AB两点间的阻值就为0。当B把圆环一分为二时，A、B两点间的阻值最大。我们可以通过二次函数的来进行验证。

AB两点把圆分为两部分，那么阻值设为R1，R2，R=R1+R2。由上图可知为并联：

由结果可以得出当R1=1/2 R是A、B两点间的阻值最大。

三、函数的单调性求极值

用单调性求极值是高中物理中最常用，最普通的数学方法，适用于求解待求量与在一定范围内变化的已知物理量之间存在直接的单调递增或者单调静摩擦力即为本题的临界条件。跟据临界值进行计算。

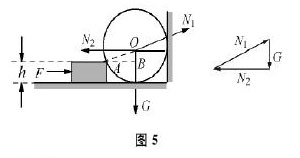
如：如图4所示，半径为R，质量为M的均匀球体紧贴竖直墙壁放置，在球体的左下方有一厚为h的木快（h

解析：球体脱离地面的临界条件是对地面的压力恰好没有，此时所需要的力F最小。对球体受力分析如图5所示，再以木块和球体组成的系统为研究对象，易知：F=N2。可见，求 F的极小值实际上就是确定N2的极小值，将图示中球体所受的三力平移组成一个矢量三角形，如图5所示，由三角形相似原理，有

即为需要的最少的推力。

四、三角函数求值法

当物理量跟数据的关系不大，题目中涉及到角度和角度的量时，我們需要用到三角函数来进行极值的求解，一般三角函数大多数在0到1之间徘徊。例如：

拖把是由拖把杆和拖把头构成的擦地工具。设拖把头的质量为m，拖把杆质量可忽略，拖把头与地板之间的动摩擦因数为常数P重力加速度为某同学用该拖把在水平地板上拖地时，沿拖把杆方向推拖把头，拖把杆与竖直方向的夹角为θ。

解：平衡可得：。N表示对拖把的压力，f表示拖把的摩擦力，

要使上式成立的θ角的取值范围。注意到上式右边总是大于零，且当F无限大时极限为零，有。

使上式成立的角满足，这里是题中所定义的极值角，即当时，不管沿拖把杆方向用多大的力都推不动拖把头。极值角的正切为。

五、总结

在进行物理极值问题时，不能想当然按照惯性思维去思考问题，需要全方面的考虑，有时题目不是困难的，而是我们忽视了其中的一个问题，从不同的角度去看，可以发现更多的想法，以上只是我个人总结的些对极值问题的看法，希望可以给其他人一个参考价值。

参考文献

[1]宋军锋.物理临界与极值问题的教学方法[J].中学物理教学参考，2009（06）

[2]周宏建.例析高中物理极值问题的求解方法[J].中学生数理化，2016（11）

[3]鲁信.高中物理极值问题求解的两种思路[J].新高考（高三理化生），2013（02）

[4]徐建.福州物理学会新编高中数理化复习参考丛书[M].天津：天津科学技术出版社，2016.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。