巧用面积法突破几何题

    覃秀芬

    

    

    

    [摘要]面积法是几何中较为特殊的思想方法，该方法可用于解决一些与线段相关的几何问题，探讨面积法的解题思路及技巧，可以提高学生的解题能力。

    [關键词]面积法，几何题，转化

    [中图分类号]G633.6[文献标识码]A [文章编号]1674-6058（2020）11-0014-02

    面积法是利用面积之间的相互转化或利用面积与边、角之间的关系来求解的一种方法，面积法在几何问题中有着广泛的应用，

    一、用面积法求线段长

    面积法可用于求线段长，求解时一般结合题干信息采用两种思路：一是若图形的面积已知，则可以结合面积公式直接转化为关于线段长的乘积;二是若图形中存在等面积关系，则可以利用等面积法完成线段乘积关系构建，

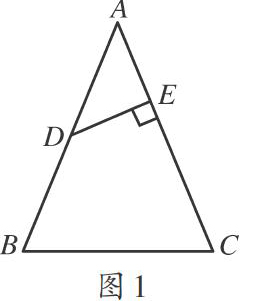
    [例1]如图1所示的△ABC为等腰三角形，其中AB=AC=13.BC=10.点D是腰AB上的中点，现过点D作AC上的垂线，垂足为点E，则线段DE的长为____，

    分析：题干表明点D是AB的中点，若过点B再作AC的垂线，令垂足为点F，则DE就为△ABF的中位线，DE长就为BF长的一半，此时可利用面积法求出BF的长，

    评析：上述面积法用到了等量转化思想，该面积模型构建的思路是建立在对几何三角形面积模型的充分认识上，也是等面积求线段长的常用方式，

    二、用面积法证明线段和差问题

    [例2]如图3所示，△ABC为等边三角形，设h表示其中一边上的高，已知点P为三角形内的任意一点，分别过点P作三角形三边上的垂线，垂足分别为点D、E、F试证明：PE+PF+PD=h。

    分析：过点P作了三条垂线，若连接PA、PB、PC，则可以将△ABC分割为三个小的三角形：△APC、△APB和△BPC，三个小三角形的面积和等于△ABC的面积，

    三、用面积法证明定理

    几何定理和公式之间存在一定的关联，实际上也可以用面积法与角平分线判定定理之间的关联完成相关问题解答，

    [例3]如图4所示的△ABM中，AE和BD分别是底边BM和AM上的高，AE与BD相交于点C，已知AE=BE，且BD是∠ABM的角平分线，试证明∠BDE=∠MDE

    分析：证明∠BDE=∠MDE就是证明ED是∠BDM的平分线，根据角平分线的判定定理可知，只需要证明点E到角两边的距离相等即可，

    四、用面积法求最值

    求最值是平面几何常见的问题类型，对于一些线段、面积最值问题有时也可以采用面积法来求解，

    [例4]如图5所示的等腰△ABC中，已知AB=AC=5.BC=6.点P是边AC上的一个动点，连接BP，试分析线段BP的最小值，

    分析：本题看似是几何动点问题，但结合“垂线段最短”知识可直接确定BP最短时的情形，即BP是边AC上的垂线时就可以满足条件，△ABC为等腰三角形，题干给出了三边长，可以通过面积法来求解，

    五、用面积法求比例

    利用面积法可以构建关于线段长的比例关系，因此可以将面积法推广到求证线段比例问题中，

    分析：如图6所示的三条直线为平行关系，需求证对应的线段比例式，实际上就是要证明平行线分线段的成比例，证明线段比例式一般有两种思路：一是构建相似三角形，利用相似性质完成;二是借用面积法，通过等面积转化来完成，本问题采用面积法。

    评析：上述在求证比例式时将等面积作为中介，借用面积公式完成了比例式转化证明，面积法的使用是建立在几何图形上的，因此，在求解线段比例问题时首先需要构建图形，然后利用面积关系来转化。