数学史融入线性代数教学的探讨

    李中 肖劲森 林全文

    

    

    摘 要：线性代数是大学数学一门重要的基础课，具有较强的抽象性与逻辑性，在线性代数的教学中融入数学史的相关内容，不仅可以培养大学生的学习兴趣，拓宽大学生的视野，而且有助于学生理解数学思想和方法，从而提高学生分析问题和解决问题的能力。

    关键词：线性代数; 数学史; 线性方程组

    中图分类号：G642? ? ? ? ? ? ? 文献标识码：A? ? 文章编号：1006-3315（2019）9-149-001

    性代数是代数学的一个分支，是高等代数的一部分。它的研究对象是向量、线性空间、线性变换和线性方程组。由于线性代数具有较强的抽象性与逻辑性，许多问题要通过繁琐的计算步骤才能解决，这使得很多学生对线性代数感到乏味枯燥，学习兴致不高，难以准确理解与掌握线性代数的基本概念和基本理论，从而不能在有限的时间内系统地掌握线性代数的基本概念、基本理论和基本方法。因此必须适当地将数学史融入线性代数的教学之中，提高学生的学习兴趣和学习积极性。

    一、将数学史融入行列式的教学中

    行列式是线性代数的入门和基础知识，是研究线性代数的一个重要工具，在线性方程组、矩阵、二次型中都要用到行列式知识。在教学中可以适当讲解行列式的发展史。据数学史记载，行列式是由德国数学家莱布尼茨和日本数学家关孝和于17世纪后半叶分别提出的。1750年，瑞士数学家克莱姆在其著作中完整、明确地给出了行列式的定义和计算方法，并给出了后人称之为解线性方程组的克莱姆法则。在克莱姆发表其著作《线性代数分析导引》后的一段时间内，行列式只是作为解线性方程组的一种工具，直到1771年，法国数学家范德蒙给出了用余子式来展开行列式的法则，此后行列式除了应用于线性方程组的求解外，并逐步单独作为线性代数的一个理论分支来研究。1812年，法国数学家柯西发现了行列式在解析几何中的应用。继柯西之后，雅可比发表了著名论文《论行列式的形成和性质》，建成了行列式的系统理论，并将其应用到除解析几何外的其他数学分支中。现在，人们对行列式应用的不断探索，行列式的应用也越来越广泛了。

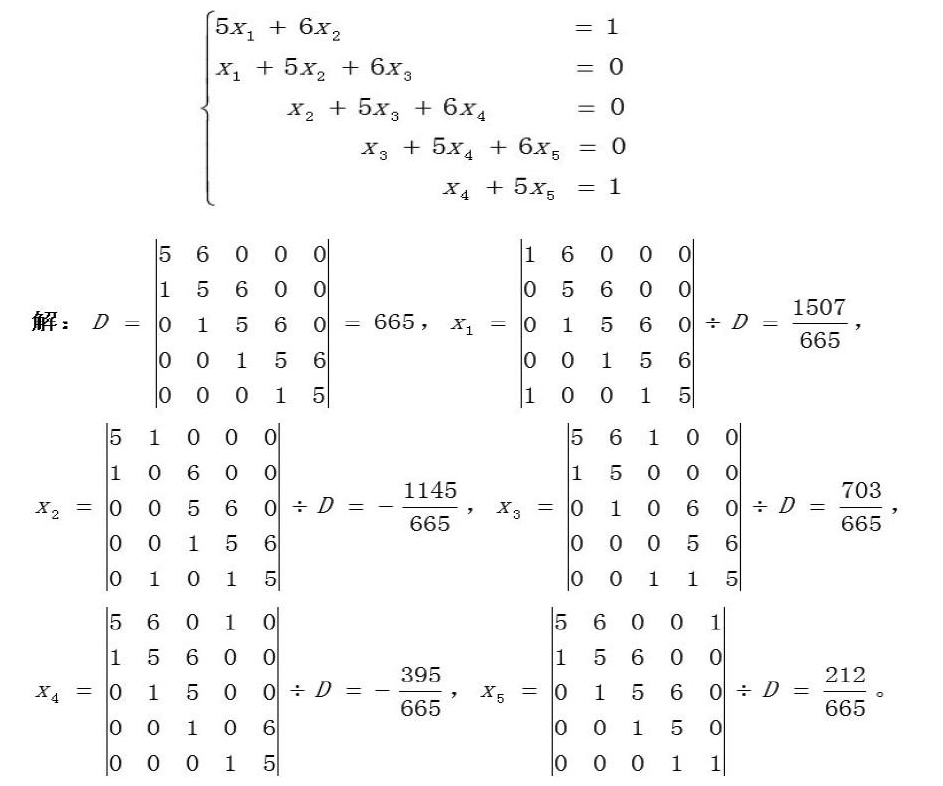
    例：用克莱姆法则解方程组

    通过上述数学史和例子的讲解，学生学习兴趣和学习积極性提高了，从而有助于学生对基本概念和基本理论的理解。

    二、矩阵论的一些数学史在教学中的作用

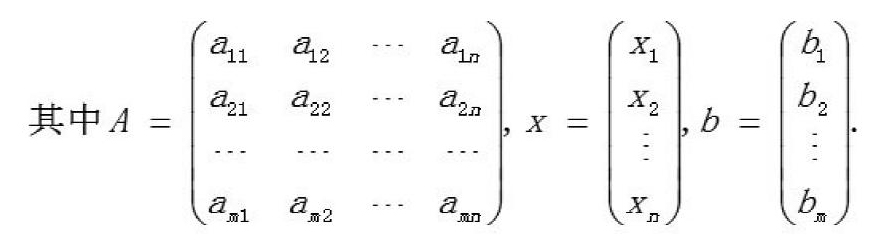
    早在公元1世纪下半叶，我国古代数学专著《九章算术》中的“方程章”就介绍了线性方程组。书中的方程组是用列表（算筹布列）的方法解之，即今之增广矩阵求解方程组，是人类历史上最早出现的线性方程组。这些数学史可以激发学生的爱国热情和民族自豪感，使学生学习线性代数的兴趣大增。到了19世纪，德国数学家高斯和爱森斯坦系统地研究了矩阵及其乘积，使矩阵作为研究数学的工具得到了完善。有了矩阵的乘法，任意一个线性方程组都可以写成向量方程的形式。例如：n元线性方程组可以写作向量方程

    将线性方程组写成向量方程的形式，可以利用系数矩阵A和增广矩阵B=（A，b）的秩来讨论线性方程组是否相容及相容时解是否唯一等问题，进而可以用初等行变换求解线性方程组。

    高斯和爱森斯坦的研究结果为英国数学家凯莱把矩阵作为一个独立的数学概念提出来并创立了矩阵论打下了坚实的基础。矩阵理论的发展，使得矩阵不但在线性代数作为一个重要工具使用，而且也是研究其他数学分支的一个重要工具。通过上述数学史的讲解，可以拓宽大学生的视野，使学生学习线性代数起到了事半功倍的效果。

    三、结语

    通过探讨数学史融入线性代数主要内容行列式和矩阵的教学，不仅可以培养学生的学习兴趣和拓宽学生的视野，加深他们对线性代数基本概念和基本理论的记忆和理解，而且有助于学生理解数学思想、理论和方法，从而提高学生的数学思维能力、创新能力和实践能力，使学生早日成为社会主义事业的建设者和接班人。

    基金项目：广东省高等学校优秀青年教师培养计划资助项目（YQ2015117）;广东石油化工学院2017年“创新强校”发展规划类入库项目（No.GYFG2017A08）;广东石油化工学院教学改革研究项目（No.214357）;数学与应用数学专业双体系人才培养模式试点（No.214404）。

    参考文献：

    [1]李文林.数学史概论第二版[M]北京：高等教育出版社，2002

    [2]同济大学应用数学系.线性代数，第四版[M]北京：高等教育出版社，2003

    [3]吴文俊.九章算术与刘徽[M]北京：北京师范大学出版社，1982

    [4]梁宗巨，王青建，孙宏安.世界数学通史（下册）[M]沈阳：辽宁教育出版社，2001