数理结合解决电学图象问题
李鸿


摘 要:电学图象是中考、竞赛中解决问题的重要工具和考查内容,利用数学中直角坐标系知识结合物理意义分析图象中的图线,通过数理结合“凑公式”利用斜率和“面积”、遵循规律“凑数字”、寻找方程“凑图线”等解决相关问题,形成解决相关电学问题通用的思维方法,并提高学生解答物理问题的思维能力.
关键词:数理结合;解决;电学图象
物理图象能方便形象地表示一个物理量随另一个物理量的变化规律,物理图象通常是利用数学中的直角坐标系来表示,在物理电学中有很多应用,是中考、竞赛的重要内容之一.
1 数理结合“凑公式”
如图1所示的数学图象中,倾斜的直线表示y与x成正比,直线的斜率k=yx.在物理图象中,横轴、纵轴表示的物理量不同,图象的物理意义不同.
在解答物理图象相关问题时,先要理解图象中的横轴、纵轴表示的物理量及其单位.图2所示图象中,倾斜直线的斜率k=yx=UI,可以“凑”成公式R=UI ,则直线斜率表示定值电阻R=U1I1=U2I2=ΔUΔI.图3所示图象中,倾斜直线斜率k=yx=IU (注意图2、图3两图象区分),可以“凑”成公式IU=1R,则直线斜率表示定值电阻的倒数(或导体的导电性能).
例1 如图4所示的电路中,电源电压保持不变,电压表和电流表的示数分别用U、I表示,定值电阻R2和整个电路消耗的电功率分别用P、P总表示.如图5所示的图象中,反映物理量之间的关系错误的是( )
分析:图中变阻器与R2串联,设电源电压为U电源、电流表示数为I、电压表示数为U,R2消耗电功率P =I 2R2=U2R2,则PI2=R2等于定值,对应图线为倾斜的直线,图A合理;P =U2R2对应数学图象y =kx 2(k为定值),对应图象为抛物线,图B合理.整个电路消耗电功率P总=U电源I =U电源 UR2,则P总I=U电源等于定值,对应的图线为倾斜的直线,图C合理;P总U等于定值,对应的图线为倾斜的直线,图D错误.
图2的U -I、图3的I-U图象中,还可以“凑”成公式P =UI,图线与横轴围成的“面积”表示电功率(某一电压下、对应的电流两点“坐标”乘积).利用此方法解题,比单纯的理论推导,思维要清晰、简洁很多.
例2 小明在进行“测量小灯泡电功率”的实验测得如下数据.你认为该灯泡“实际电压是额定电压一半时的电功率P1”和“实际电流是额定电流一半时的电功率P2”的大小关系是P1P2(选填“大于”、“小于”或“等于”).
分析:根据实验数据或实验经验画出如图所示的图象,图6中阴影面积表示实际电压为额定电压一半时的电功率P1,图7中阴影面积表示实际电流为额定电流一半时的电功率P2(实际作图中,可以将两图作在一个图中,便于比较),显然P1>P2.
2 遵循规律 “凑数字 ”
如图8、9所示的图象中,曲线都表示y随x增大而增大,但图8中的y随x增大的越来越快,图9中的y随x增大的越来越慢(虚线表示曲线上该点的切线对应斜率).图10、13中的曲线表示用电器的电阻随电压的增大而增大,图11、12中的曲线表示用电器的电阻随电压的增大而减小.
对于曲线,其规律只能“点”(该点对应的横坐标)与“点”(该点对应的纵坐标)对应.在串联电路中,如果只有两个元件,元件有图11~13中的曲线(如果两元件的电流和电压关系在两个图象中,将两元件的电流和电压关系画在同一图中,可以有效地分析和解答问题),可以根据串联电路中电流相等的规律,分析图中电流相等线(对应的直线)与图中的图线的交点坐标(对应的电压),只有能“凑”成两电压之和等于电源电压的才是符合要求的“点”.
在并联电路中,如果只有两个元件,分析图中电压相等线(对应的直线)与图中的图线的的交点坐标(对应的电流),只有能“凑”成两支路的电流之和等于干路电流的才是符合要求的“点”.
例3 如图14甲所示,当开关S接a时,移动滑动变阻器的滑片P,根据测出的电流、电压值,画出了定值电阻R0的U-I图象;当开关S接b时,同样根据测出的电流、电压值,画出了灯泡L的U-I图象,如图乙所示.
(1)求定值电阻R0的阻值;
(2)将R0与灯L串联接在6 V的电源两端时,求灯丝的实际电阻值;
(3)将R0与灯L并联接入电路并调节电源电压,当R0消耗的电功率为4.9W时,灯L恰好正常发光,求灯L的额定电功率.
分析:解答“将R0与灯L串联接在6V的电源两端”一类题的关键是利用“串联电路中电流相等、总电压等于各元件两端电压之和”的特点,利用图象中电流相等(0.4A竖直线)上对应的电压(2V、4V)之和为6V两个特殊点“凑数字”来解答.
解:(1)由图乙知:U0=2V时,I0=0.2A
∴R0=U0I0=10Ω
(2)分析图象可知R0与L串联接在6 V电源两端时,IL=0.4A,灯两端电压UL=2V
∴RL=ULIL=5Ω
(3)R0與L并联接入电源,R0两端电压
U0′=PR0=4.9W×10Ω=7V
∵R0与RL并联且灯正常发光
∴UL额=U0′=7V
由图象可知此时:IL额=0.75A
∴L额定功率
PL额=UL额IL额=7V×0.75A=5.25W
3 寻找方程“凑图线”
数学中,如果已知函数关系式,可以用描点法在图象中画出相应的图象.如果电学中的两个物理量符合函数关系式(可以结合物理知识求出这个关系式),数学图象就变成对应的物理图象,“凑”成需要的图线,再利用图线来解决问题.
例4 如图15甲所示为一灯泡两端的电压与通过它的电流的变化关系曲线.如图乙所示,将两个这样的灯泡并联后再与10Ω的定值电阻R0串联,接在电压为8V的电源上(不计电流表和电源的内阻),求:通过电流表的电流值以及每个灯泡的实际功率.
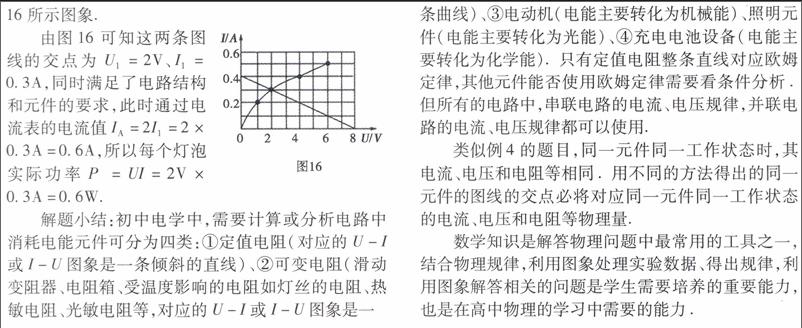
分析:由图甲中灯泡的伏安特性曲线知灯泡的电阻温度升高而增大.设图乙中每个灯泡两端电压为U、电流为I,由并联电路电流规律知电流表示数为2I,电阻R0两端电压为2IR0,则电源电压U总=U +2IR0,再将U总=8V、R0=10Ω代入上式整理得一次函数U =8-20I,采用描点法把该直线图15上画出,可得图16所示图象.
由图16可知这两条图线的交点为U1=2V、I1=0.3A,同时满足了电路结构和元件的要求,此时通过电流表的电流值IA=2I1=2×0.3A=0.6A,所以每个灯泡实际功率P =UI=2V×0.3A=0.6W.
解题小结:初中电学中,需要计算或分析电路中消耗电能元件可分为四类:①定值电阻(对应的U-I或I-U图象是一条倾斜的直线)、②可变电阻(滑动变阻器、电阻箱、受温度影响的电阻如灯丝的电阻、热敏电阻、光敏电阻等,对应的U-I或I-U图象是一条曲线)、③电动机(电能主要转化为机械能)、照明元件(电能主要转化为光能)、④充电电池设备(电能主要转化为化学能).只有定值电阻整条直线对应欧姆定律,其他元件能否使用欧姆定律需要看条件分析.但所有的电路中,串联电路的电流、电压规律,并联电路的电流、电压规律都可以使用.
类似例4的题目,同一元件同一工作状态时,其电流、电压和电阻等相同.用不同的方法得出的同一元件的图线的交点必将对应同一元件同一工作状态的电流、电压和电阻等物理量.
数学知识是解答物理问题中最常用的工具之一,结合物理规律,利用图象处理实验数据、得出规律,利用图象解答相关的问题是学生需要培养的重要能力,也是在高中物理的学习中需要的能力.



摘 要:电学图象是中考、竞赛中解决问题的重要工具和考查内容,利用数学中直角坐标系知识结合物理意义分析图象中的图线,通过数理结合“凑公式”利用斜率和“面积”、遵循规律“凑数字”、寻找方程“凑图线”等解决相关问题,形成解决相关电学问题通用的思维方法,并提高学生解答物理问题的思维能力.
关键词:数理结合;解决;电学图象
物理图象能方便形象地表示一个物理量随另一个物理量的变化规律,物理图象通常是利用数学中的直角坐标系来表示,在物理电学中有很多应用,是中考、竞赛的重要内容之一.
1 数理结合“凑公式”
如图1所示的数学图象中,倾斜的直线表示y与x成正比,直线的斜率k=yx.在物理图象中,横轴、纵轴表示的物理量不同,图象的物理意义不同.
在解答物理图象相关问题时,先要理解图象中的横轴、纵轴表示的物理量及其单位.图2所示图象中,倾斜直线的斜率k=yx=UI,可以“凑”成公式R=UI ,则直线斜率表示定值电阻R=U1I1=U2I2=ΔUΔI.图3所示图象中,倾斜直线斜率k=yx=IU (注意图2、图3两图象区分),可以“凑”成公式IU=1R,则直线斜率表示定值电阻的倒数(或导体的导电性能).
例1 如图4所示的电路中,电源电压保持不变,电压表和电流表的示数分别用U、I表示,定值电阻R2和整个电路消耗的电功率分别用P、P总表示.如图5所示的图象中,反映物理量之间的关系错误的是( )
分析:图中变阻器与R2串联,设电源电压为U电源、电流表示数为I、电压表示数为U,R2消耗电功率P =I 2R2=U2R2,则PI2=R2等于定值,对应图线为倾斜的直线,图A合理;P =U2R2对应数学图象y =kx 2(k为定值),对应图象为抛物线,图B合理.整个电路消耗电功率P总=U电源I =U电源 UR2,则P总I=U电源等于定值,对应的图线为倾斜的直线,图C合理;P总U等于定值,对应的图线为倾斜的直线,图D错误.
图2的U -I、图3的I-U图象中,还可以“凑”成公式P =UI,图线与横轴围成的“面积”表示电功率(某一电压下、对应的电流两点“坐标”乘积).利用此方法解题,比单纯的理论推导,思维要清晰、简洁很多.
例2 小明在进行“测量小灯泡电功率”的实验测得如下数据.你认为该灯泡“实际电压是额定电压一半时的电功率P1”和“实际电流是额定电流一半时的电功率P2”的大小关系是P1P2(选填“大于”、“小于”或“等于”).
分析:根据实验数据或实验经验画出如图所示的图象,图6中阴影面积表示实际电压为额定电压一半时的电功率P1,图7中阴影面积表示实际电流为额定电流一半时的电功率P2(实际作图中,可以将两图作在一个图中,便于比较),显然P1>P2.
2 遵循规律 “凑数字 ”
如图8、9所示的图象中,曲线都表示y随x增大而增大,但图8中的y随x增大的越来越快,图9中的y随x增大的越来越慢(虚线表示曲线上该点的切线对应斜率).图10、13中的曲线表示用电器的电阻随电压的增大而增大,图11、12中的曲线表示用电器的电阻随电压的增大而减小.
对于曲线,其规律只能“点”(该点对应的横坐标)与“点”(该点对应的纵坐标)对应.在串联电路中,如果只有两个元件,元件有图11~13中的曲线(如果两元件的电流和电压关系在两个图象中,将两元件的电流和电压关系画在同一图中,可以有效地分析和解答问题),可以根据串联电路中电流相等的规律,分析图中电流相等线(对应的直线)与图中的图线的交点坐标(对应的电压),只有能“凑”成两电压之和等于电源电压的才是符合要求的“点”.
在并联电路中,如果只有两个元件,分析图中电压相等线(对应的直线)与图中的图线的的交点坐标(对应的电流),只有能“凑”成两支路的电流之和等于干路电流的才是符合要求的“点”.
例3 如图14甲所示,当开关S接a时,移动滑动变阻器的滑片P,根据测出的电流、电压值,画出了定值电阻R0的U-I图象;当开关S接b时,同样根据测出的电流、电压值,画出了灯泡L的U-I图象,如图乙所示.
(1)求定值电阻R0的阻值;
(2)将R0与灯L串联接在6 V的电源两端时,求灯丝的实际电阻值;
(3)将R0与灯L并联接入电路并调节电源电压,当R0消耗的电功率为4.9W时,灯L恰好正常发光,求灯L的额定电功率.
分析:解答“将R0与灯L串联接在6V的电源两端”一类题的关键是利用“串联电路中电流相等、总电压等于各元件两端电压之和”的特点,利用图象中电流相等(0.4A竖直线)上对应的电压(2V、4V)之和为6V两个特殊点“凑数字”来解答.
解:(1)由图乙知:U0=2V时,I0=0.2A
∴R0=U0I0=10Ω
(2)分析图象可知R0与L串联接在6 V电源两端时,IL=0.4A,灯两端电压UL=2V
∴RL=ULIL=5Ω
(3)R0與L并联接入电源,R0两端电压
U0′=PR0=4.9W×10Ω=7V
∵R0与RL并联且灯正常发光
∴UL额=U0′=7V
由图象可知此时:IL额=0.75A
∴L额定功率
PL额=UL额IL额=7V×0.75A=5.25W
3 寻找方程“凑图线”
数学中,如果已知函数关系式,可以用描点法在图象中画出相应的图象.如果电学中的两个物理量符合函数关系式(可以结合物理知识求出这个关系式),数学图象就变成对应的物理图象,“凑”成需要的图线,再利用图线来解决问题.
例4 如图15甲所示为一灯泡两端的电压与通过它的电流的变化关系曲线.如图乙所示,将两个这样的灯泡并联后再与10Ω的定值电阻R0串联,接在电压为8V的电源上(不计电流表和电源的内阻),求:通过电流表的电流值以及每个灯泡的实际功率.
分析:由图甲中灯泡的伏安特性曲线知灯泡的电阻温度升高而增大.设图乙中每个灯泡两端电压为U、电流为I,由并联电路电流规律知电流表示数为2I,电阻R0两端电压为2IR0,则电源电压U总=U +2IR0,再将U总=8V、R0=10Ω代入上式整理得一次函数U =8-20I,采用描点法把该直线图15上画出,可得图16所示图象.
由图16可知这两条图线的交点为U1=2V、I1=0.3A,同时满足了电路结构和元件的要求,此时通过电流表的电流值IA=2I1=2×0.3A=0.6A,所以每个灯泡实际功率P =UI=2V×0.3A=0.6W.
解题小结:初中电学中,需要计算或分析电路中消耗电能元件可分为四类:①定值电阻(对应的U-I或I-U图象是一条倾斜的直线)、②可变电阻(滑动变阻器、电阻箱、受温度影响的电阻如灯丝的电阻、热敏电阻、光敏电阻等,对应的U-I或I-U图象是一条曲线)、③电动机(电能主要转化为机械能)、照明元件(电能主要转化为光能)、④充电电池设备(电能主要转化为化学能).只有定值电阻整条直线对应欧姆定律,其他元件能否使用欧姆定律需要看条件分析.但所有的电路中,串联电路的电流、电压规律,并联电路的电流、电压规律都可以使用.
类似例4的题目,同一元件同一工作状态时,其电流、电压和电阻等相同.用不同的方法得出的同一元件的图线的交点必将对应同一元件同一工作状态的电流、电压和电阻等物理量.
数学知识是解答物理问题中最常用的工具之一,结合物理规律,利用图象处理实验数据、得出规律,利用图象解答相关的问题是学生需要培养的重要能力,也是在高中物理的学习中需要的能力.

