巧用“一题多变”突破浮力难点

    罗小飞

    

    

    

    [摘要]“浮力”是初中科学教学中的重难点，对知识的综合和思维的灵动等要求都很高。学生在学习浮力时兴趣并不浓厚，畏惧心很强，对相应知识的认识只知其一，不知其二，思維窄，稍有变化就无计可施。针对以上情况，巧妙利用“一题多变”可以灵活整合相关知识，将“浮力”难点逐个击破，从而激活学生的思维，培养学生的核心素养。

    [关键词]浮力;一题多变;思维;核心素养

    [中图分类号]G633.98 [文献标识码]A [文章编号]1674-6058（2020）05-0085-04

    “浮力”是初中科学中最具魅力、最变幻莫测、最具挑战性的一模块内容。为了啃掉这块硬骨头，许多教师可谓煞费苦心，有的用题海战术，有的用模型战术，有的用公式战术，可是不论采取哪种战术，学生一遇到稍微灵活点的浮力问题，依然手足无措。“浮力”让师生都陷入了身心俱疲的难堪境地。

    常言道：“变则通，通则达。”一次大胆的尝试，让笔者寻找到了一个新的解决办法——“一题多变”。“一题多变”是数学教学常用的一种方法，对思维的拓展和提升能起到推波助澜的作用，其在科学教学中也可收到神奇的效果。“一题多变”可让学生经历“求同存异”的辩证性思维训练，提升分析与综合、逻辑与推理、类比与创新等高阶思维，水到渠成地培养学生的科学学科核心素养，尤其是科学思维。将“一题多变”运用于“浮力”的教学，可让“浮力”以“阿基米德原理”为主线，以“受力分析”为辅线，双线螺旋式上升，成功突破教学难点。下面笔者谈谈如何巧用“一题多变”突破浮力难点。

    一、“一题多变”突破浮力难点之“体积”问题

    浮力中求解“排开液体的体积”，是“阿基米德原理”和“受力分析”两大难点相结合的题型，此类题型非常典型，学生虽然经常遇到，但是一旦稍有难度，依然会难以驾驭。教师可将“一题多变”融入“比比液面高低”这样的趣味情境中，让学生积极参与层层递进的“变式训练”，进而实现思维的节节攀升。

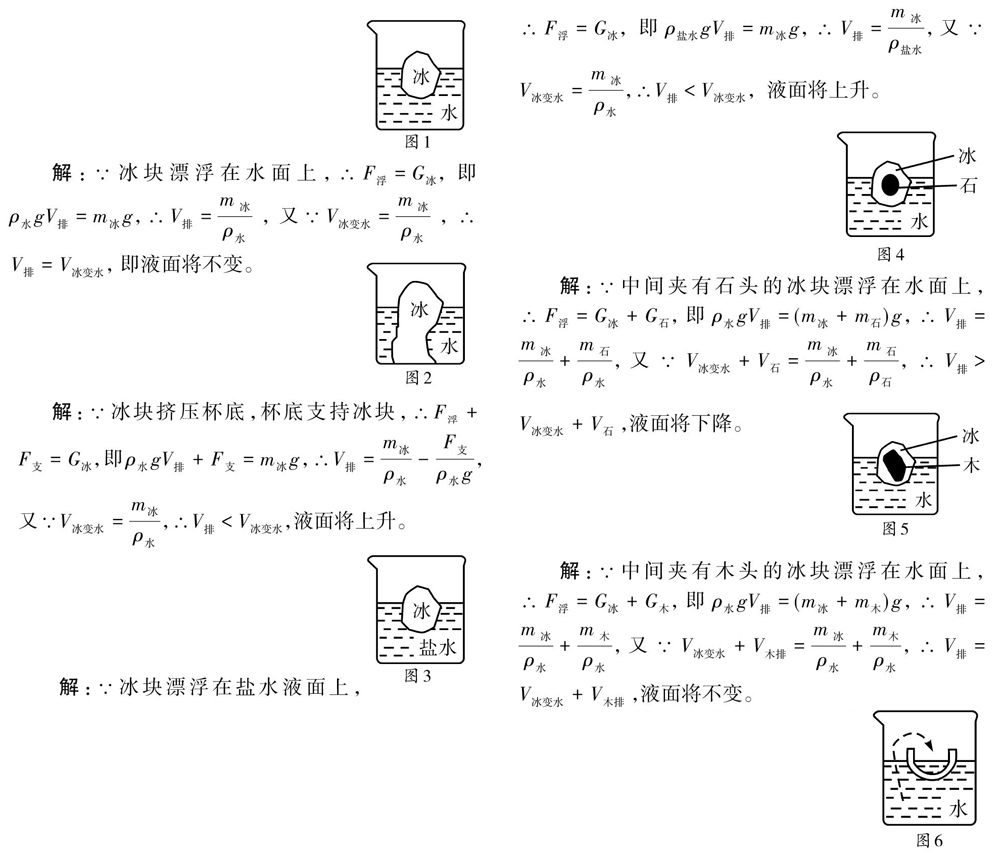
    【典型例题1】如图1.烧杯中盛有一定量的水，有一冰块漂浮在水面上，当冰完全熔化后液面将一（填“上升”“下降”或“不变”）。

    【变式1】如图2.烧杯中盛有一定量的水，有一冰块在水中，且下表面对杯底有压力，当冰完全熔化后液面将__（填“上升”“下降”或“不变”）。

    【变式3】如图4.烧杯中盛有一定量的水，有一中间夹石头的冰块漂浮在水面上，当冰完全熔化后液面将一（填“上升”“下降”或“不变”）。

    【变式4】如图5.烧杯中盛有一定量的水，有一中间夹木头的冰块漂浮在水面上，当冰完全熔化后液面将__（填“上升”“下降”或“不变”）。

    【变式5】如图6.烧杯中盛有一定量的水，有一只塑料碗漂浮在水面上，将烧杯中的部分水舀入塑料碗中（碗依然漂浮），液面将__（填“上升”“下降”或“不变”）。

    【变式6】如图7.烧杯中盛有一定量的水，有一物块沉在水底，又有一只塑料碗漂浮在水面上，现将烧杯中的物块捞起放入塑料碗中（碗依然漂浮），液面将__（填“上升”“下降”或“不变”）。

    二、“一题多变”突破浮力难点之“密度”问题

    浮力中求解“浸在液体中物体的密度”和“液体的密度”也是比较常见的题型，它融合了“平衡力法求浮力”“称重法求浮力”“阿基米德原理法求浮力”以及“受力分析”。此类题型变幻莫测，非常具有挑战性。教师可以迎合学生的挑战欲望，巧妙地将“一题多变”融入“冲关我最棒”这样的游戏挑战情境中，让学生积极参与“变式挑战”活动，进而挑战自己的思维极限。

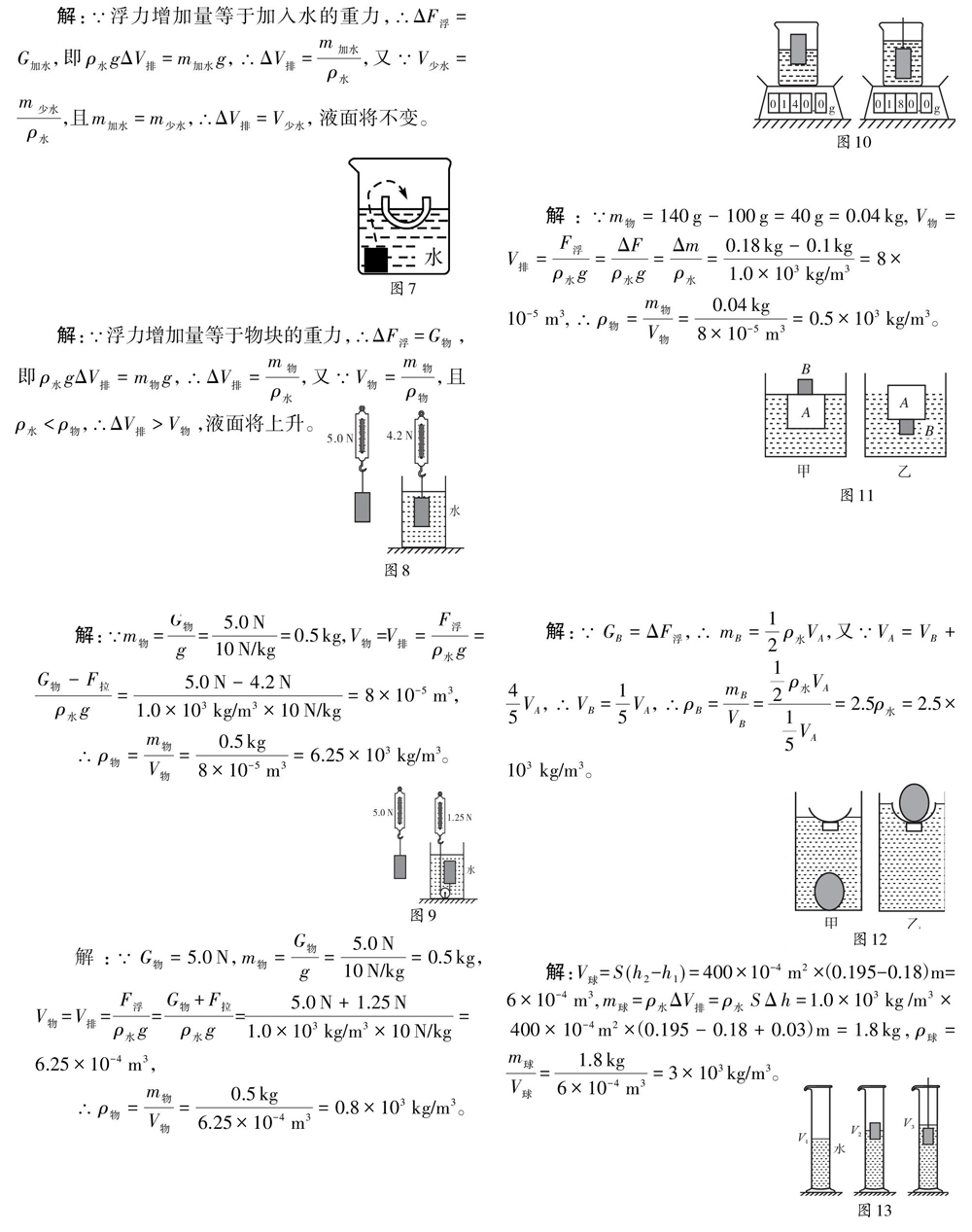
    【典型例题2】如图8.先用弹簧测力计测出实心物块在空气中的重力为5.0 N，再将实心物块浸没在水中，此时弹簧测力计的示数为4.2 N，求实心物块的密度。（g取10N/kg）

    【变式1】如图9.先用弹簧测力计测出实心物块在空气中的重力为5.0 N，再利用定滑轮将实心物块浸没在水中，此时弹簧测力计的示数为1.25 N，求实心物块的密度。（g取10 N/kg）

    【变式2】如图10.烧杯中倒入适量的水，放上电子秤称出质量为100 g，然后放入一实心塑料块，示数为140 g，再用一个力将塑料块完全浸没时，示数为180 g，请问塑料块的密度是多少？（g取10 N/kg）

    【变式3】在一个圆柱形容器内盛有深为20 cm的水，现将一质量为200 g的密闭空心铁盒A放入水中，空心铁盒有一半浮出水面;当铁盒上放一个小磁铁B时，铁盒恰好浸没水中，如图11甲所示;当把它们倒置在水中时，A有1/5的体积露出水面，如图11乙所示，小磁铁B的密度为__kg/m2。

    【变式4】有学生用学过的科学知识测一个金属球的密度。他找来了圆柱形容器、刻度尺和一个塑料小碗。把圆柱形容器放在水平桌面上并在其中装入适量的水，让塑料小碗漂浮在水面上，此时容器内的水深为18 cm。当把金属球放入容器内的水中时，容器内的水深为19.5 cm，如图12甲所示。现将金属球取出后放入塑料小碗中，静止时如图12乙所示。乙图中的水面比甲图中的水面高3 cm。已知：容器的内部底面积为400 cm2，则金属球的密度是__kg/m3。

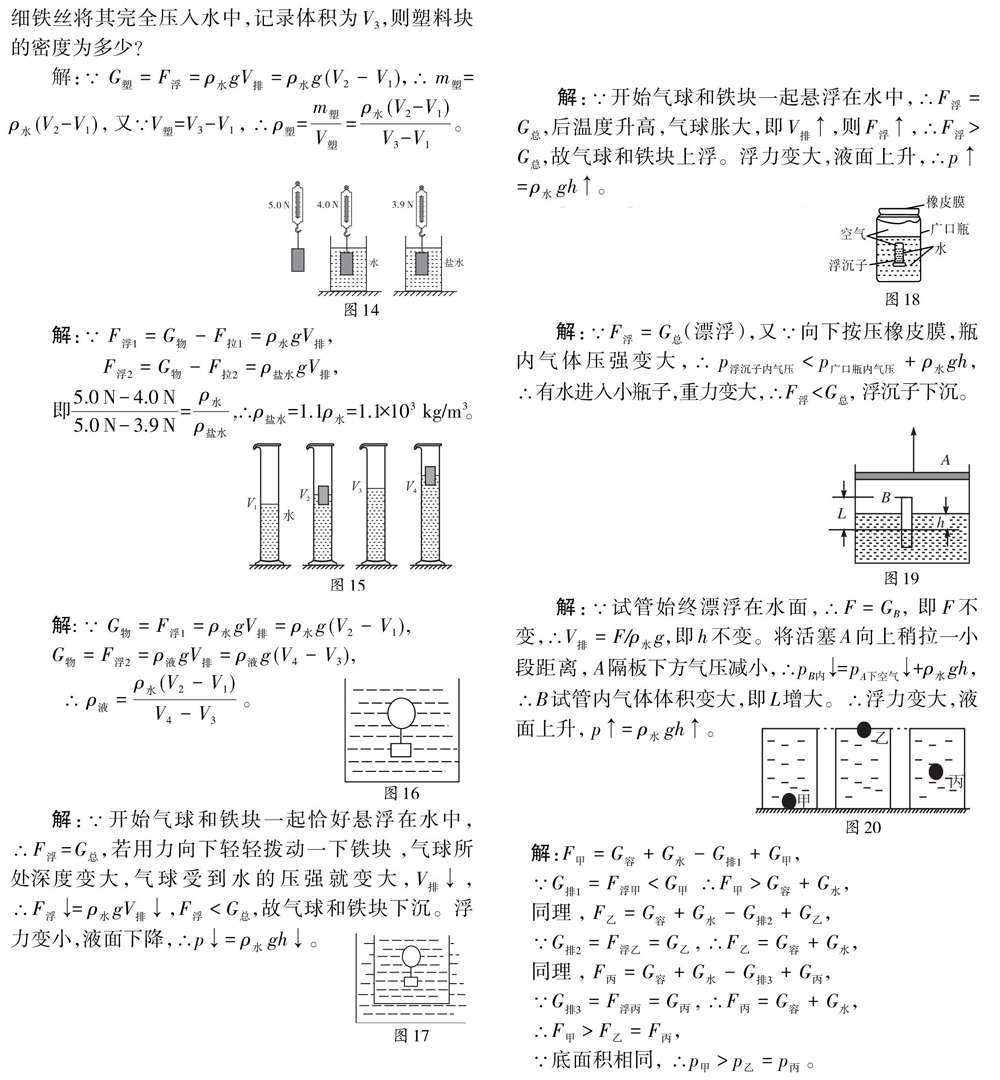
    【变式5】如图13.在量筒中放入适量的水，记录体积为V1.然后将一实心塑料块放入量筒，当其漂浮时，记录体积为V2.然后用细铁丝将其完全压入水中，记录体积为V3.则塑料块的密度为多少？

    【变式6】如图14.先用弹簧测力计测出实心物块在空气中的重力为5.0 N，然后将物块浸没在水中，此时弹簧测力计的示数为4.0 N，再将物块浸没在盐水中，弹簧测力计的示数为3.9 N，求实心物块的密度。

    【变式7】如图15.量筒中放入适量水，体积为V1.让一轻质物体漂浮在量筒的水里，水面到达的刻度为V2;量筒中放待测液体，体积为V3.再让同一个轻质物体漂浮在量筒中的液体里，液面到达的刻度为V4.则待测液体的密度为多少？

    三、“一题多变”突破浮力难点之“沉浮”问题

    “沉浮”问题，说白了就是比较重力和浮力的大小，然而其融合“阿基米德原理”和“壓力、压强”等知识后就很具变换性和挑战性了。此类题型内藏玄机，趣味盎然，教师可以巧妙地将“一题多变”融入“魔性沉浮”这样的趣味情境中，让学生享受“一题多变”带来的快乐。

    【典型例题3】用细绳连在一起的气球和铁块，恰能悬浮在盛水的圆柱形容器内如图16所示位置。若用力向下轻轻拨动一下铁块，则气球和铁块的沉浮情况及水对容器底部的压强将如何变化？

    【变式1】用细绳连在一起的气球和铁块，恰能悬浮在盛水的圆柱形容器内如图17所示位置，若用水浴微微加热，则气球和铁块的沉浮情况及水对容器底部的压强将如何变化？

    【变式2】如图18.一个广口瓶里面装着一个用倒放的小瓶子制作成的浮沉子，广口瓶中装有一定量的水，瓶口用橡皮膜封住，开始时小瓶子是漂浮的，若向下按压橡皮膜会观察到什么现象？

    【变式3】如图19.圆筒内盛有水，水的上方被活塞A密封住一部分空气，一试管B开口朝下，竖直漂浮在水面上，管内封有一段长为L的空气柱，试管所受浮力为F，管内外水面高度差为h，现将活塞A向上稍拉一小段距离后，试管又重新平衡（试管内气体没有溢出），h、L、F如何变化？

    【变式4】如图20.将体积相同、材料不同的甲、乙、丙三个实心小球，分别轻轻放入三个装满水的相同烧杯中，甲球下沉至杯底、乙球漂浮和丙球悬浮，比较各烧杯对桌面压强的大小。

    四、“一题多变”突破浮力难点之“图像”问题

    浮力中的“图像”问题对学生思维的要求很高，它需要学生根据图像想象运动情景，并建立模型，然后再分析受力情况，且综合运用“阿基米德原理”“沉浮条件”“压力、压强”等来解决相应问题。此类题型灵活多变，难度颇大。教师可以巧妙地将“一题多变”融入“美图秀秀”自主创作情境中，让学生享受“一题多变”带来的思维冲浪。

    【典型例题4】如图21甲所示，在容器底部固定一轻质弹簧，弹簧上方连有正方体木块A，容器侧面的底部有一个阀门B，此时木块A刚好完全浸没在水中，接着打开阀门B，缓慢放水，直至木块A完全离开水面时，再关闭阀门B，这个过程中，弹簧弹力F与木块露出水面的体积V的关系如图21乙所示。（已知p水=1.0×103kg/m3，p木=0.7×103kg/m3，木块体积为Vo不计弹簧所受浮力）求：（1）D点的横坐标d值为多少？（2）点C与点E的纵坐标c、e的绝对值之比为多少？

    例题讲解后，请学生画一画对应其他物理量的“变式图像”（如图22、图23和图24），并以“美图秀秀”的形式来呈现，让学生自己体验“一题多变”带来的快乐。

    为了更好地锻炼学生的逆向思维，教师可以将“放水”改成“注水”，让学生饶有兴趣地去逆向探索，以发展学生的科学思维。

    【逆向思维例题】如图25甲所示，高5 cm、重4 N的长方体物块被弹簧固定在烧杯底部。现向烧杯中缓缓加水，水位高度H随时间变化如图25乙所示。（整个过程中，弹簧每受到1N的力，伸长或压缩1 cm，弹簧所受的浮力忽略不计）

    讲解逆向思维例题后，也请学生画一画对应其他物理量的“变式图像”（如图27、图28和图29），这时学生已经有了经验，再次亲自参与“一题多变”的创作，内心便会获得满满的成就感。

    综上可知，运用“一题多变”可有效突破浮力难点，很好地激活学生的科学思维，全面提升学生分析与综合、逻辑与推理、类比与创新等高阶思维，真正培养了学生的科学学科核心素养。