负整数指数幂简便运算规律的探究及归纳
黄小燕
【摘要】负整数指数幂的运算主要运用了负整数指数幂的性质a-p=1ap(a≠0,p是正整数),但在运算的过程中,当底数a是负数、分数时,学生解题相当困难,特别是当对底数为负分数时,要顾虑括号,还要考虑指数的奇偶导致结果符号正负不同的问题等,非常头疼.本文将对负整数指数幂的运算规律加以探究并归纳,希望能为学生的学习带来帮助.
【关键词】负整数指数幂;简便运算;运算规律
俗话说的好,授之以鱼不如授之以渔.在教学的过程中,尤其是理科的教学,教师教会学生解一道题,不如教会学生解一类题,更不如教会学生更好的解题方法.初一的学生在学习幂运算,特别是负整数指数幂运算的时候,由于认知能力不够成熟,逻辑思维能力也比较薄弱,导致对负整数指数幂的运算性质理解不透彻,对运算公式的特征辨识度也不高,因此记忆模糊,运用起来相当困难,错漏百出,只有你想不到的错误,没有他不出现的错误.这不仅让学生的学习非常困难,甚至痛苦,老师也为学生忧心忡忡.因此,对负整数指数幂简便运算规律的探索研究显得尤为必要和紧急.为此,本文将展开对负整数指数幂简便运算规律的探索.
1规律的发现
《义务教育数学课程标准(2011年版)》中强调数学教学要注重对学生数学思想方法的教育.其中化未知为已知的化归思想是初中阶段数学教学中非常重要的一种思想.生物学也告诉我们,人的生理、认知发展是循序渐进的,每个人对接触过的、熟知的事物的理解能力、接收能力都较陌生事物容易、简单.因此,若能把学生感到陌生的负整数指数幂转化为他们熟知的正整数指数幂运算,那么学生对该知识的理解和掌握就会变得非常简单、轻松.
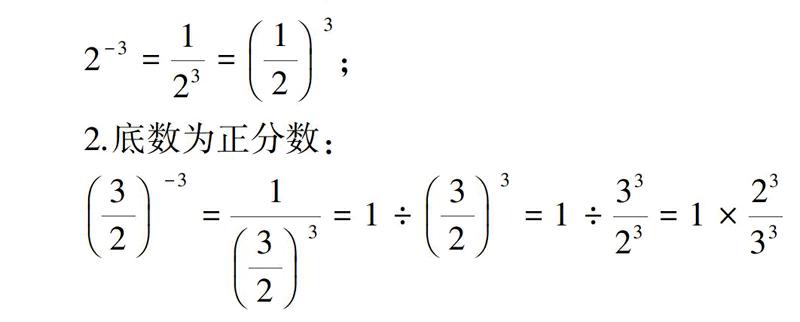
1.底数为正整数:
2-3=123=123;

2.底數为正分数:
32-3=1323=1÷323=1÷3323=1×2333=233;
3.底数为负整数:
-4-3=1-43=1-43=-143=-143=-143;
4.底数为负分数:
-34-5=1-345=1÷-3455=-1×4535=-435=-435.
下面我们再仔细观察上面四个式子:
①2-3=123;②32-3=233;
③-4-3=-143;④-34-5=-435;
我们发现,无论底数是正整数、正分数、负整数、负分数的负整数指数幂运算,其在运算过程中都存在这样的规律:底数转变成它的倒数,指数则变成它的相反数,即:a-p=1apa≠0,p是正整数.可见,a-p=1ap(a≠0,p是正整数)相较a-p=1ap(a≠0,p是正整数),计算结果简便了许多,当a为分数时,不再出现重分数、多括号的情况,学生也不用过多的担心符号正负的问题,这会让运算过程变得容易理解和操作.
2规律运用的先进性
马克思主义理论告诉我们,检验理论的唯一标准就是实践,在具体的数学实践之中真正能够使得某些运算更加简便、精确的方法才会得到全面的推广,下面我们通过几个例子,将课本方法和运用规律运算的简便方法进行鲜明对比,感受一下此规律在实践中的可操作性和先进性.

例1 计算38÷13-6.
课本方法简便方法38÷13-6简便方法:38÷13-6.解原式
= 38÷1136
=38×136
=32×36×136
= 9×3×136
=9. 解原式
= 38÷36
= 32
= 9.通过例1运用的两种不同的运算方法的鲜明对比,我们发现:利用课本方法求解,在运算过程中出现了比较繁琐的重分数,如:38÷1136,对于这类式子的变形和运算,正是学生很难理解的地方,所以往往运算到这一步的时候就会被卡住,无从下手.使用简便的去处规律,我们可以轻轻松松的避免繁琐的重分数,直接转化成学生熟悉的同底数幂相除,即可轻松获取最终答案.
例2计算14×-12-2.
课本方法简便方法解:原式
= 14×1-122
= 14×1÷-122
= 14×4
=1.解:原式
= 14×-22
= 14×4
= 1.例2的求解中,我们发现利用课本方法求解的过程中,不仅仅出现了重分数,还出现了中括号,这意味着学生需要考虑符号以及括号内部的整体问题,难度再次加大了!但运用简便方法的运算,在第1步就将重分数、括号问题解决掉,并将负整数指数幂巧妙转化成正整数指数幂,计算量小,难度小,易懂易掌握.

很显然,在探索出新规律之后,负整数指数幂的运算变得非常简单,运算过程中不再出现繁琐的重分数、多括号、符号正负不同等问题,为学生解决了烦恼,还大大降低了运算的错误率,学生也能很好地理解和掌握,最后运用于实践解决实际问题.
3规律的延伸
在探索过程中,我们发现此规律在科学记数法以及部分同底数幂除法的运算中衍生出了新的简便运算规律,在数学的举一反三的思想引领下,继续探究,下面通过例子说明:
例3 计算
1÷2.5×10-9.
解原式
= 1÷2.5÷10-9
= 0.4÷1109
=0.4×109
= 4×108.例4 计算
2÷10-8.
解原式
= 2÷1108
= 2×108.通过观察上面两个例子,我们发现将当除以一个以10为底的负整数指数幂的时候,可以将除法转化为乘法,指数则变成它的相反数,即:a÷10-p=a×10p(p为正整数),例:2÷10-8=2×108.
如果除数的底数不是10呢,上述运算规律仍然成立.
例5计算:
20÷-12-2.
解原式
=1÷1-122
=1×-122
=14. 例6计算
138÷3-6.
解原式
=138÷136
=138×36
=19.下面再仔細观察一下上面两个式子:
①20÷-12-2=1×-122;
② 138÷3-6=138×36.
观察上列式子可见,无论除数的底数为任意负数、正数、分数或整数,任意有理数a除以任何非零数b的负整数指数幂,其结果都等于乘以这个数b的正整数指数幂,其中b的指数-p变成它的相反数p,即:a÷b-p=a×bp(b≠0,p为正整数).
此外,最后一个运算规律a÷b-p=a×bp(b≠0,p为正整数)并不是在所有的运算式子中都是最简便的,例如本文中的例6,相较而言,采用第一个简便运算规律a-p=1ap(a≠0,p是正整数)时,反而使运算更加简单.因此,学生在运算负整数指数幂的过程中也许多观察、总结,在不同的式子中选择最简便的方法才是最明智的.
4总结
北师大版教材中,初一的知识以数与代数为主,学生每天都需要跟本来就很枯燥无味的数字打交道,还要在原本非常简单的数字中去理解、分析、掌握它们之间形成的变幻莫测的公式,这对初中生而言是有一定难度的,尤其在遇到负整数指数幂运算这样难度较大的运算时,学生恐之惶之,严重地打击了学生的自信心和学习数学的兴趣.本文对负整数指数幂简便运算规律的探究和归纳,在投入到教学实践推广运用的过程中,绝大部分的学生能够正确理解并掌握精髓,还能在实践中屡试不爽,极大的激发了学生对数学研究的热情,激发了学生学习数学的兴趣和自信心,也给予学生更多坚持下去的力量,充分体现了《课程标准》中强调的学生为本的人文主义精神,让学生快乐学习.
通过文中众多例子以及实际的教学效果来看,本文所探究归纳得出的两个负整数指数幂运算规律的实用性很强,把学生感觉陌生的负整数指数幂非常巧妙的转化为他们非常熟悉的正整数指数幂进行运算,变繁琐的重分数、多括号、多符号等问题为简单的分数、整数的正整数指数幂运算,通俗易懂,可操作、可推广,希望对学生的学习有所裨益.
【摘要】负整数指数幂的运算主要运用了负整数指数幂的性质a-p=1ap(a≠0,p是正整数),但在运算的过程中,当底数a是负数、分数时,学生解题相当困难,特别是当对底数为负分数时,要顾虑括号,还要考虑指数的奇偶导致结果符号正负不同的问题等,非常头疼.本文将对负整数指数幂的运算规律加以探究并归纳,希望能为学生的学习带来帮助.
【关键词】负整数指数幂;简便运算;运算规律
俗话说的好,授之以鱼不如授之以渔.在教学的过程中,尤其是理科的教学,教师教会学生解一道题,不如教会学生解一类题,更不如教会学生更好的解题方法.初一的学生在学习幂运算,特别是负整数指数幂运算的时候,由于认知能力不够成熟,逻辑思维能力也比较薄弱,导致对负整数指数幂的运算性质理解不透彻,对运算公式的特征辨识度也不高,因此记忆模糊,运用起来相当困难,错漏百出,只有你想不到的错误,没有他不出现的错误.这不仅让学生的学习非常困难,甚至痛苦,老师也为学生忧心忡忡.因此,对负整数指数幂简便运算规律的探索研究显得尤为必要和紧急.为此,本文将展开对负整数指数幂简便运算规律的探索.
1规律的发现
《义务教育数学课程标准(2011年版)》中强调数学教学要注重对学生数学思想方法的教育.其中化未知为已知的化归思想是初中阶段数学教学中非常重要的一种思想.生物学也告诉我们,人的生理、认知发展是循序渐进的,每个人对接触过的、熟知的事物的理解能力、接收能力都较陌生事物容易、简单.因此,若能把学生感到陌生的负整数指数幂转化为他们熟知的正整数指数幂运算,那么学生对该知识的理解和掌握就会变得非常简单、轻松.
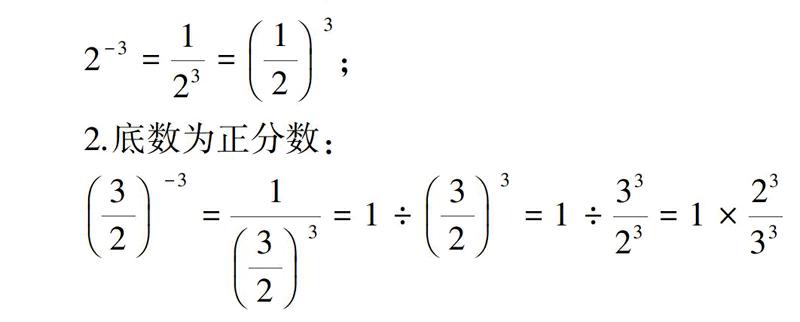
1.底数为正整数:
2-3=123=123;

2.底數为正分数:
32-3=1323=1÷323=1÷3323=1×2333=233;
3.底数为负整数:
-4-3=1-43=1-43=-143=-143=-143;
4.底数为负分数:
-34-5=1-345=1÷-3455=-1×4535=-435=-435.
下面我们再仔细观察上面四个式子:
①2-3=123;②32-3=233;
③-4-3=-143;④-34-5=-435;
我们发现,无论底数是正整数、正分数、负整数、负分数的负整数指数幂运算,其在运算过程中都存在这样的规律:底数转变成它的倒数,指数则变成它的相反数,即:a-p=1apa≠0,p是正整数.可见,a-p=1ap(a≠0,p是正整数)相较a-p=1ap(a≠0,p是正整数),计算结果简便了许多,当a为分数时,不再出现重分数、多括号的情况,学生也不用过多的担心符号正负的问题,这会让运算过程变得容易理解和操作.
2规律运用的先进性
马克思主义理论告诉我们,检验理论的唯一标准就是实践,在具体的数学实践之中真正能够使得某些运算更加简便、精确的方法才会得到全面的推广,下面我们通过几个例子,将课本方法和运用规律运算的简便方法进行鲜明对比,感受一下此规律在实践中的可操作性和先进性.

例1 计算38÷13-6.
课本方法简便方法38÷13-6简便方法:38÷13-6.解原式
= 38÷1136
=38×136
=32×36×136
= 9×3×136
=9. 解原式
= 38÷36
= 32
= 9.通过例1运用的两种不同的运算方法的鲜明对比,我们发现:利用课本方法求解,在运算过程中出现了比较繁琐的重分数,如:38÷1136,对于这类式子的变形和运算,正是学生很难理解的地方,所以往往运算到这一步的时候就会被卡住,无从下手.使用简便的去处规律,我们可以轻轻松松的避免繁琐的重分数,直接转化成学生熟悉的同底数幂相除,即可轻松获取最终答案.
例2计算14×-12-2.
课本方法简便方法解:原式
= 14×1-122
= 14×1÷-122
= 14×4
=1.解:原式
= 14×-22
= 14×4
= 1.例2的求解中,我们发现利用课本方法求解的过程中,不仅仅出现了重分数,还出现了中括号,这意味着学生需要考虑符号以及括号内部的整体问题,难度再次加大了!但运用简便方法的运算,在第1步就将重分数、括号问题解决掉,并将负整数指数幂巧妙转化成正整数指数幂,计算量小,难度小,易懂易掌握.

很显然,在探索出新规律之后,负整数指数幂的运算变得非常简单,运算过程中不再出现繁琐的重分数、多括号、符号正负不同等问题,为学生解决了烦恼,还大大降低了运算的错误率,学生也能很好地理解和掌握,最后运用于实践解决实际问题.
3规律的延伸
在探索过程中,我们发现此规律在科学记数法以及部分同底数幂除法的运算中衍生出了新的简便运算规律,在数学的举一反三的思想引领下,继续探究,下面通过例子说明:
例3 计算
1÷2.5×10-9.
解原式
= 1÷2.5÷10-9
= 0.4÷1109
=0.4×109
= 4×108.例4 计算
2÷10-8.
解原式
= 2÷1108
= 2×108.通过观察上面两个例子,我们发现将当除以一个以10为底的负整数指数幂的时候,可以将除法转化为乘法,指数则变成它的相反数,即:a÷10-p=a×10p(p为正整数),例:2÷10-8=2×108.
如果除数的底数不是10呢,上述运算规律仍然成立.
例5计算:
20÷-12-2.
解原式
=1÷1-122
=1×-122
=14. 例6计算
138÷3-6.
解原式
=138÷136
=138×36
=19.下面再仔細观察一下上面两个式子:
①20÷-12-2=1×-122;
② 138÷3-6=138×36.
观察上列式子可见,无论除数的底数为任意负数、正数、分数或整数,任意有理数a除以任何非零数b的负整数指数幂,其结果都等于乘以这个数b的正整数指数幂,其中b的指数-p变成它的相反数p,即:a÷b-p=a×bp(b≠0,p为正整数).
此外,最后一个运算规律a÷b-p=a×bp(b≠0,p为正整数)并不是在所有的运算式子中都是最简便的,例如本文中的例6,相较而言,采用第一个简便运算规律a-p=1ap(a≠0,p是正整数)时,反而使运算更加简单.因此,学生在运算负整数指数幂的过程中也许多观察、总结,在不同的式子中选择最简便的方法才是最明智的.
4总结
北师大版教材中,初一的知识以数与代数为主,学生每天都需要跟本来就很枯燥无味的数字打交道,还要在原本非常简单的数字中去理解、分析、掌握它们之间形成的变幻莫测的公式,这对初中生而言是有一定难度的,尤其在遇到负整数指数幂运算这样难度较大的运算时,学生恐之惶之,严重地打击了学生的自信心和学习数学的兴趣.本文对负整数指数幂简便运算规律的探究和归纳,在投入到教学实践推广运用的过程中,绝大部分的学生能够正确理解并掌握精髓,还能在实践中屡试不爽,极大的激发了学生对数学研究的热情,激发了学生学习数学的兴趣和自信心,也给予学生更多坚持下去的力量,充分体现了《课程标准》中强调的学生为本的人文主义精神,让学生快乐学习.
通过文中众多例子以及实际的教学效果来看,本文所探究归纳得出的两个负整数指数幂运算规律的实用性很强,把学生感觉陌生的负整数指数幂非常巧妙的转化为他们非常熟悉的正整数指数幂进行运算,变繁琐的重分数、多括号、多符号等问题为简单的分数、整数的正整数指数幂运算,通俗易懂,可操作、可推广,希望对学生的学习有所裨益.

