借助密克定理再探锐角三角形内所能包含的最大正方形问题
1背景介绍
图1题目(2013 天津)如图1,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
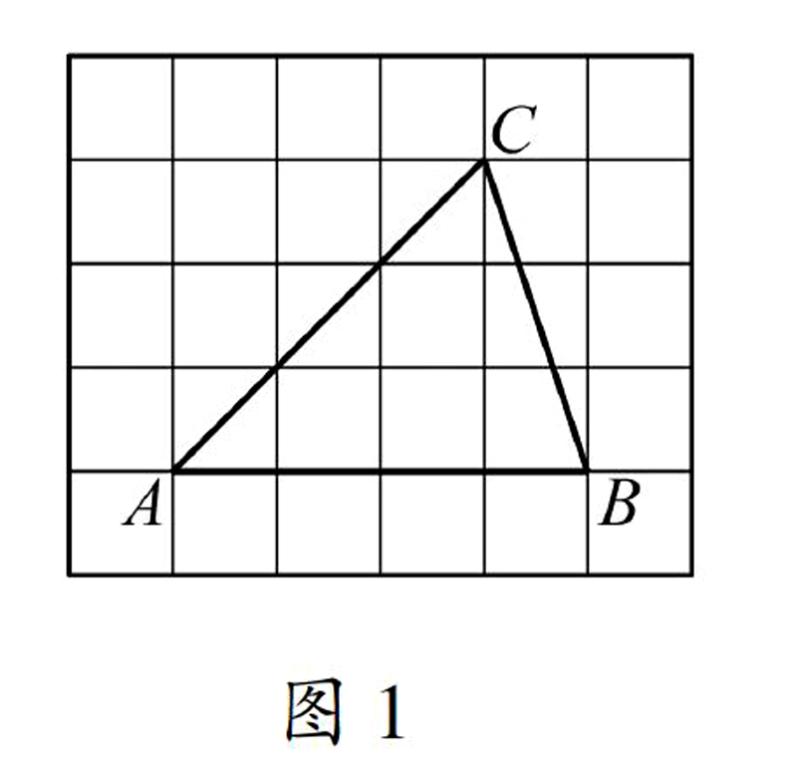
(Ⅰ)△ABC的面积等于 ;
(Ⅱ)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图的方法(不要求证明).
本题是2013年天津市中考数学卷的第18题,该题的第(Ⅱ)问设计精巧,内涵可谓极其丰富.但是很多文章对该问的解答都回避了一个问题,即为什么△ABC中所能包含的面积最大的正方形一定是△ABC的内接正方形?或者说,如果一个正方形只有三个顶点分别落在△ABC的三条边上,那么这样的正方形为什么不可能是最大的?终于,两年多之后,文[1](下称“原文”)针对这个问题做了比较详尽的解答,读来令人激动万分!细细品味该文后,针对这个问题笔者从另一个角度作了进一步思考,现将本人的思考整理成文,以就教于同行.
2构造更具一般性的三个顶点分别落在△ABC的三条边上的正方形
图2原文中,为了说明三个顶点分别落在△ABC的三条边上的正方形的存在性,先作∠ABC的平分线交AC于点D,如图2,过点D分别作AB、BC的垂线段DE、DF,在AB、BC上分别取点G、H,使得∠EDG=∠FDH=12(90°-∠ABC),再过点G作DH的平行线交BD于点K,连接HK(原文为“过点H做DG的平行线”,不够严谨),易证四边形DGKH为正方形.
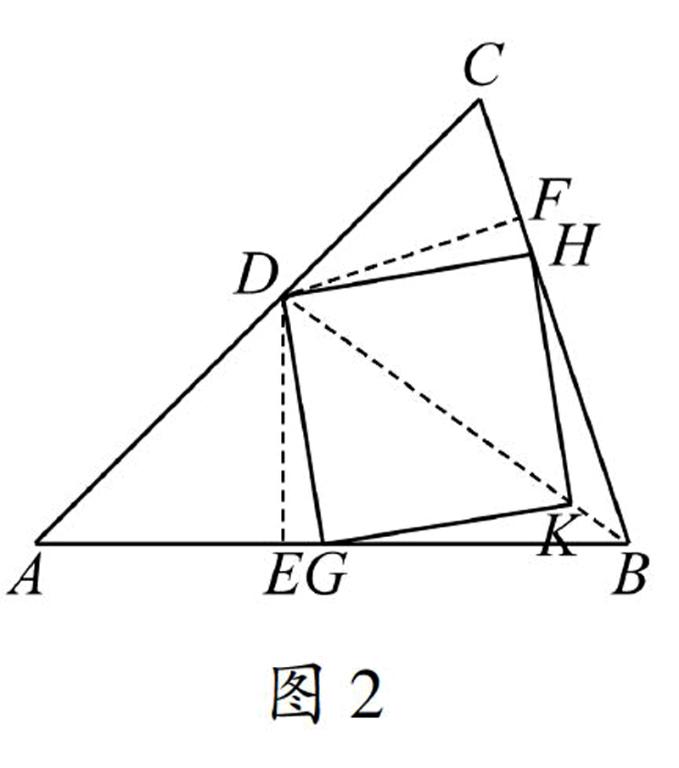
显然,此时的∠AGD是一个定值,但在随后的代数推理過程中(原文换了字母)又被当成一个变量(∠B≤∠AGD≤90°),那么问题来了,原本∠AGD是固定的,当它发生变化时,四边形DGKH还是一个正方形吗?如果是,又如何保证它的三个顶点分别落在△ABC的三条边上且第四个顶点在△ABC的内部呢?换句话说,如何构造更具一般性的三个顶点分别落在△ABC的三条边上的正方形?笔者对此进行了深入的思考,发现可以多次利用位似图形放大,直至有三个顶点分别落在△ABC的三条边上,现展示具体作法.
图3图4图5图6如图3,作一直线MN与△ABC的两边分别交于M、N,且∠B≤∠ANM≤90°,在线段MN上取适当的两点D、E,在直线MN的右侧作正方形DEFG,且该正方形包含于△ABC(类似两圆的位置关系);接下来,将正方形DEFG连续位似放大,作直线DF、EG交于点O,它们与△ABC的三边交于B1、B2、B3、B4四点,如图4,比较ODOB1、OEOB2、OFOB3、OGOB4中的最小值,不妨设OEOB2最小,以点O为位似中心,将正方形DEFG逐渐放大直至点E与点B2重合;作射线ED、EF交AC、BC于C1、C2,如图5,同样,比较EC1ED、EB4EG、EC2EF中的最小值,不妨设EC1ED最小,以点E为位似中心,将正方形DEFG逐渐放大直至点D与点B1重合;作射线AG、AF交BC于D1、D2,如图6,比较AD1AG和AD2AF的大小,不妨设AD2AF较小,以点A为位似中心,将正方形DEFG逐渐放大直至点F与点D2重合.
通过以上有限的步骤可知,当∠B<∠ANM<90°时,可以得到一个只有三个顶点分别落在△ABC的三条边上且第四个顶点在△ABC内部的正方形,相比于原文中构造的正方形更具一般性;而当∠ANM=90°-∠C或 90°时,正方形DEFG内接于△ABC.同时,不难发现,这一构造的过程也回答了为什么只要比较原文中的(5)(6)两种情形.原文证明情形(5)不可能最大的方法偏重于代数推理,不够直观,那么有没有更直观的方法呢?这再度引起了笔者的思考.
3利用密克定理使证明过程更直观化
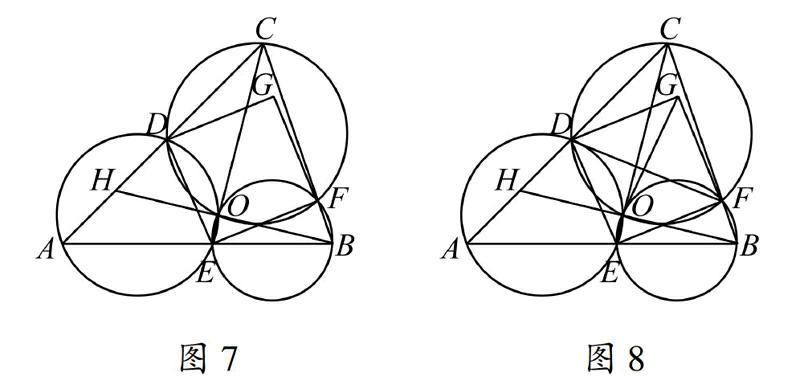
由于有三个顶点分别落在△ABC的三条边上,这让笔者联想到了密克定理,即在一个三角形的每一条边上各取一点,过三角形的每一个顶点与两条邻边上所取的点作圆,则这三个圆共点(其证明过程非常简单,参见文[2]).如图7,作出这样的三个圆,由密克定理可知,它们交于一点,设该点为O,连接AO、BO、CO,延长BO交AC于点H,由三角形的外角性质得,∠AOB=∠OAH+∠OHA=∠OAH+∠ACB+∠CBH,连接OE,根据“同弧所对的圆周角相等”可得,∠OAH+∠ACB+∠CBH=∠ACB+∠DEO+∠OEF=∠ACB+∠DEF=∠ACB+90°,即∠AOB=∠ACB+90°.同理可得,∠AOC=∠ABC+90°,∠BOC=∠BAC+90°,因为△ABC的三个内角都是定值,所以∠AOB、∠AOC和∠BOC也是定值,从而可以得到这样一个结论:当∠AED在其取值范围内发生变化时,点O是△ABC内的一个定点(实为三条弧形轨迹的公共点,可参考文献[3]).
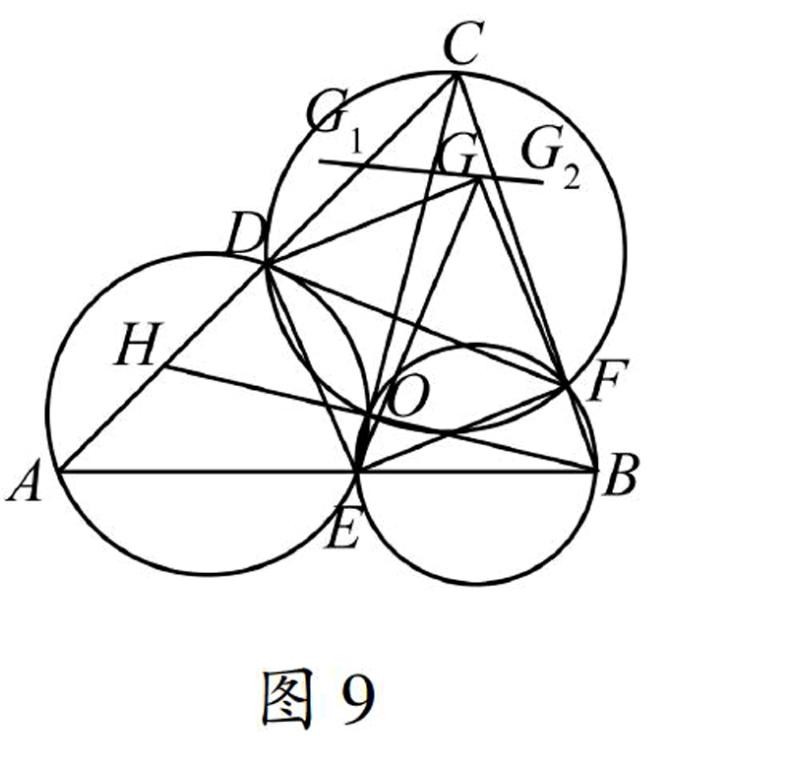
图7图8进一步,连接DO、FO和DF,如图8,根据“圆的内接四边形对角互补”可得,∠DOF=180°-∠ACB,∠DOE=180°-∠BAC,∠EOF=180°-∠ABC,显然∠DOF、∠DOE和∠EOF也是定值,因此,点O在等腰Rt△DEF亦即正方形DEFG内的相对位置是不发生变化的.连接OG,由相似性质可知,线段OD、OE、OF和OG两两之间的夹角和比值都是定值,此时,我们可以发现,正方形DEFG实际上是以点O为中心作旋转位似放缩运动.由于点D、E、F都是在直线上运动,根据文[4]的结论可知,点G也在一条直线上运动,同时,点O分别到该直线和直线AB的垂线段的长度之比等于OGOE图9且它们的夹角等于∠EOG.设该直线分别与AC、BC交于点G1、G2,如图9,那么点G的轨迹就是线段G1G2,当OG取最大值时,正方形DEFG的面积最大,此时,点G必与点G1、G2中的一点重合,即正方形DEFG是△ABC的内接正方形.下面的工作就是比较△ABC的三个不同内接正方形的大小,本文不再赘述.
4写在最后
笔者一直关注对原题解答的相关文献,遗憾的是,这些文献都是探讨内接正方形的作法和理论基础,以及所涉及的思想方法、几何模型等等,对为什么要作内接正方形避而不谈.可喜的是,向老师的文章作了可谓开拓性的尝试,这也激发了本人对该问题探究到底的决心!
与原文相比,本文更偏向于揭示几何关系结构,将原文所揭示的代数关系结构转化为更直观的几何关系结构,或者说,将“代数结构的抽象”转化成了“几何结构的直观”(文[5]),使人对问题的本质有了直观的感知和体验.
以上就是笔者对锐角三角形内所能包含的最大正方形这一问题的心得体会,不足之处,还望得到专家的批评指正!
参考文献
[1]向中军.对一道中考题的再思考[J].中学数学教学参考(中旬),2016(1-2):134-136.
[2]R.A.约翰逊.近代欧式几何学[M].单墫译.上海:上海教育出版社,1999:111-112.
[3]王成刚.明理才能得法善思方可纵深——一道作图题的解法探究[J].中学数学教学参考(中旬),2016(11):33-35.
[4]张建权.一道动态型中考题的再探究[J].中学数学教学参考(中旬),2017(3):67-68.
[5]钱德春,高荣兴.从必然到自然 从或然到应然——读文《“增解”从何而来》有感[J].中学数学教学参考(中旬),2016(7):18-22.
图1题目(2013 天津)如图1,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.

(Ⅰ)△ABC的面积等于 ;
(Ⅱ)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图的方法(不要求证明).
本题是2013年天津市中考数学卷的第18题,该题的第(Ⅱ)问设计精巧,内涵可谓极其丰富.但是很多文章对该问的解答都回避了一个问题,即为什么△ABC中所能包含的面积最大的正方形一定是△ABC的内接正方形?或者说,如果一个正方形只有三个顶点分别落在△ABC的三条边上,那么这样的正方形为什么不可能是最大的?终于,两年多之后,文[1](下称“原文”)针对这个问题做了比较详尽的解答,读来令人激动万分!细细品味该文后,针对这个问题笔者从另一个角度作了进一步思考,现将本人的思考整理成文,以就教于同行.
2构造更具一般性的三个顶点分别落在△ABC的三条边上的正方形
图2原文中,为了说明三个顶点分别落在△ABC的三条边上的正方形的存在性,先作∠ABC的平分线交AC于点D,如图2,过点D分别作AB、BC的垂线段DE、DF,在AB、BC上分别取点G、H,使得∠EDG=∠FDH=12(90°-∠ABC),再过点G作DH的平行线交BD于点K,连接HK(原文为“过点H做DG的平行线”,不够严谨),易证四边形DGKH为正方形.

显然,此时的∠AGD是一个定值,但在随后的代数推理過程中(原文换了字母)又被当成一个变量(∠B≤∠AGD≤90°),那么问题来了,原本∠AGD是固定的,当它发生变化时,四边形DGKH还是一个正方形吗?如果是,又如何保证它的三个顶点分别落在△ABC的三条边上且第四个顶点在△ABC的内部呢?换句话说,如何构造更具一般性的三个顶点分别落在△ABC的三条边上的正方形?笔者对此进行了深入的思考,发现可以多次利用位似图形放大,直至有三个顶点分别落在△ABC的三条边上,现展示具体作法.
图3图4图5图6如图3,作一直线MN与△ABC的两边分别交于M、N,且∠B≤∠ANM≤90°,在线段MN上取适当的两点D、E,在直线MN的右侧作正方形DEFG,且该正方形包含于△ABC(类似两圆的位置关系);接下来,将正方形DEFG连续位似放大,作直线DF、EG交于点O,它们与△ABC的三边交于B1、B2、B3、B4四点,如图4,比较ODOB1、OEOB2、OFOB3、OGOB4中的最小值,不妨设OEOB2最小,以点O为位似中心,将正方形DEFG逐渐放大直至点E与点B2重合;作射线ED、EF交AC、BC于C1、C2,如图5,同样,比较EC1ED、EB4EG、EC2EF中的最小值,不妨设EC1ED最小,以点E为位似中心,将正方形DEFG逐渐放大直至点D与点B1重合;作射线AG、AF交BC于D1、D2,如图6,比较AD1AG和AD2AF的大小,不妨设AD2AF较小,以点A为位似中心,将正方形DEFG逐渐放大直至点F与点D2重合.

通过以上有限的步骤可知,当∠B<∠ANM<90°时,可以得到一个只有三个顶点分别落在△ABC的三条边上且第四个顶点在△ABC内部的正方形,相比于原文中构造的正方形更具一般性;而当∠ANM=90°-∠C或 90°时,正方形DEFG内接于△ABC.同时,不难发现,这一构造的过程也回答了为什么只要比较原文中的(5)(6)两种情形.原文证明情形(5)不可能最大的方法偏重于代数推理,不够直观,那么有没有更直观的方法呢?这再度引起了笔者的思考.
3利用密克定理使证明过程更直观化
由于有三个顶点分别落在△ABC的三条边上,这让笔者联想到了密克定理,即在一个三角形的每一条边上各取一点,过三角形的每一个顶点与两条邻边上所取的点作圆,则这三个圆共点(其证明过程非常简单,参见文[2]).如图7,作出这样的三个圆,由密克定理可知,它们交于一点,设该点为O,连接AO、BO、CO,延长BO交AC于点H,由三角形的外角性质得,∠AOB=∠OAH+∠OHA=∠OAH+∠ACB+∠CBH,连接OE,根据“同弧所对的圆周角相等”可得,∠OAH+∠ACB+∠CBH=∠ACB+∠DEO+∠OEF=∠ACB+∠DEF=∠ACB+90°,即∠AOB=∠ACB+90°.同理可得,∠AOC=∠ABC+90°,∠BOC=∠BAC+90°,因为△ABC的三个内角都是定值,所以∠AOB、∠AOC和∠BOC也是定值,从而可以得到这样一个结论:当∠AED在其取值范围内发生变化时,点O是△ABC内的一个定点(实为三条弧形轨迹的公共点,可参考文献[3]).
图7图8进一步,连接DO、FO和DF,如图8,根据“圆的内接四边形对角互补”可得,∠DOF=180°-∠ACB,∠DOE=180°-∠BAC,∠EOF=180°-∠ABC,显然∠DOF、∠DOE和∠EOF也是定值,因此,点O在等腰Rt△DEF亦即正方形DEFG内的相对位置是不发生变化的.连接OG,由相似性质可知,线段OD、OE、OF和OG两两之间的夹角和比值都是定值,此时,我们可以发现,正方形DEFG实际上是以点O为中心作旋转位似放缩运动.由于点D、E、F都是在直线上运动,根据文[4]的结论可知,点G也在一条直线上运动,同时,点O分别到该直线和直线AB的垂线段的长度之比等于OGOE图9且它们的夹角等于∠EOG.设该直线分别与AC、BC交于点G1、G2,如图9,那么点G的轨迹就是线段G1G2,当OG取最大值时,正方形DEFG的面积最大,此时,点G必与点G1、G2中的一点重合,即正方形DEFG是△ABC的内接正方形.下面的工作就是比较△ABC的三个不同内接正方形的大小,本文不再赘述.

4写在最后
笔者一直关注对原题解答的相关文献,遗憾的是,这些文献都是探讨内接正方形的作法和理论基础,以及所涉及的思想方法、几何模型等等,对为什么要作内接正方形避而不谈.可喜的是,向老师的文章作了可谓开拓性的尝试,这也激发了本人对该问题探究到底的决心!
与原文相比,本文更偏向于揭示几何关系结构,将原文所揭示的代数关系结构转化为更直观的几何关系结构,或者说,将“代数结构的抽象”转化成了“几何结构的直观”(文[5]),使人对问题的本质有了直观的感知和体验.
以上就是笔者对锐角三角形内所能包含的最大正方形这一问题的心得体会,不足之处,还望得到专家的批评指正!
参考文献
[1]向中军.对一道中考题的再思考[J].中学数学教学参考(中旬),2016(1-2):134-136.
[2]R.A.约翰逊.近代欧式几何学[M].单墫译.上海:上海教育出版社,1999:111-112.
[3]王成刚.明理才能得法善思方可纵深——一道作图题的解法探究[J].中学数学教学参考(中旬),2016(11):33-35.
[4]张建权.一道动态型中考题的再探究[J].中学数学教学参考(中旬),2017(3):67-68.
[5]钱德春,高荣兴.从必然到自然 从或然到应然——读文《“增解”从何而来》有感[J].中学数学教学参考(中旬),2016(7):18-22.

