由一道“工程问题”教学引发的思考
涂爱玲++梁艳云?オ?
“工程问题”是非常典型的数学应用类问题.从小学到初中,从算式到方程,从整式方程到分式方程,每一学段的代数应用题都会涉及到“工程问题”,然而,随着问题情境的不断变更,条件的不断变换,使得问题类型不再明朗,数量关系不再清晰,甚至错综复杂,难以理清,从而导致学生对应用类问题的学习出现明显的两极分化,致使不少学生对应用题看题生畏.出现以上情况的原因,除了应用题本身的综合性强,对学生的理解能力、生活阅历要求很高之外,还跟学段知识的局限有关,同时也与老师就题论题的教学方式有密切关系.本文案例选自于湘教版八上《15可化为一元一次方程的分式方程》第二课时.这节课的教学,笔者不再采用以往的教学模式:根据问题列出分式方程,求解、检验、回答;而是打破分式方程的限制,引导学生从不同的角度寻找数量关系,建立不同类型的方程(或方程组).下面以“工程问题”为例,谈谈应用题教学中的解题策略.1教学案例

21“一题多解”打破思维禁锢
波利亚指出:“掌握数学就是善于解题.”一题多解就是启发和引导学生从不同角度不同思路分析问题,从题目中尽可能的挖掘隐含条件,采用不同的方法不同的运算过程去解决问题,最终达到异曲同工的目的.在本案例中,笔者鼓励学生从不同角度思考,通过“一题多解”打破思维禁锢,突破解题瓶颈,形成开阔的解题路径.下面用方法导图展示解题路径.
方法导图:
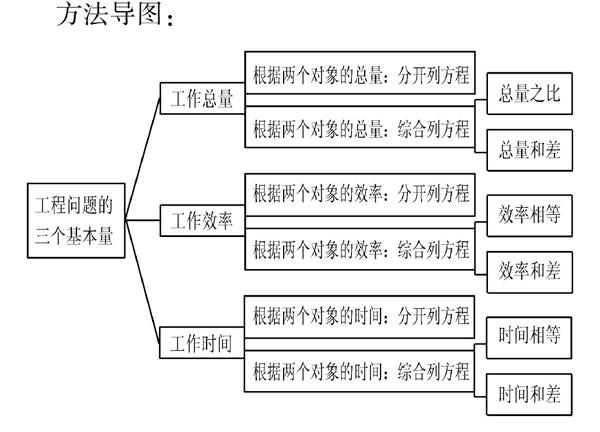
22“一表多用”建立思维联系
应用题教学既是教师授课的难点,也是学生学习的难点.究其原因:(1)问题情境复杂;(2)数量关系隐蔽;(3)未知数选择灵活.这就需要学生首先要从复杂的问题情境中剔除无效的信息干扰,提炼有效的解题信息,这是一个去情景化实现数学抽象的过程.然后需要学生处理解题信息,将各量关系从文字语言向符号语言转换,实现隐性数量关系显性化的程序.在列方程的问题转换环节,学生往往可以借助线段图、表格等进行数量关系的分析.本案例采用表格将文字语言转换为图表语言,使得数量关系直观化、数量化,有效建立起多维度思考的桥梁.下面用列表导图展示解题思路.
列表导图:
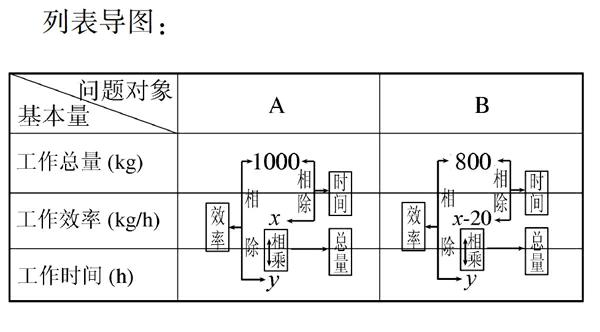
2.3“多元歸一”揭示思维本质
“工程问题”的“一题多解”归根结底是对基本关系式:工作总量=工作时间×工作效率的变形使用,用其中的两个量表示第三个量;抓住其中的一个量建立方程,又可沿着:分开列方程和综合列方程展开;而综合列方程又可沿着:相等→和差→比例等角度展开,多种途径只因一个基本关系,可谓九九归一.“工程问题”的“解题策略”可归结为以下四步:第一步,明确问题类型;第二步,确定基本关系;第三步,写出关系列表;第四步,列出方程求解.整个流程形成了一个思维链.对于“工程问题”的解题策略和解题方法不仅仅局限于“工程问题”,与之关联的还有“行程问题”、“销售问题”、“利润问题”、“浓度问题”、“面积问题”等等,只要基本关系中涉及到三个量之间的积或商的关系均可.综上所述,由“工程问题”的解题研究引发的一系列思考,让我们不难发现应用题解题是一个系统工程,其中蕴含“一题多解”、“一法多用”、“多题归一”的数学思想,对培养学生的发射性思维和归纳演绎能力颇有益处.唯有认清问题的本质,才能突破解题的局限,长此以往方能去繁就简,优化解题方法.下面是对本案例研究的整体思维导图,让我们认清思维之间的联系.
案例研究思维导图:
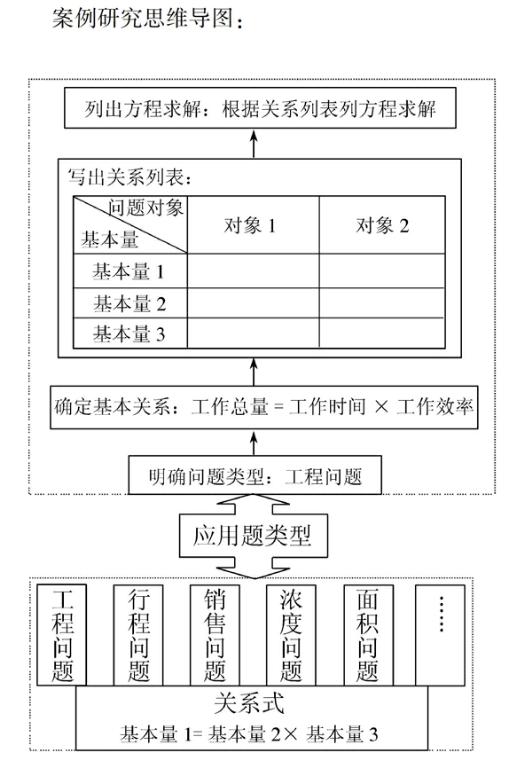
作者简介涂爱玲(1976—),女,广西桂林人,中学高级教师,桂林市优秀教师,广西国培、区培优秀讲师.主要研究变式教学.撰写《中学数学变式教学问题设计与课例研究》,编写了两套变式教学教辅书,发表论文13篇,获奖论文30余篇.
“工程问题”是非常典型的数学应用类问题.从小学到初中,从算式到方程,从整式方程到分式方程,每一学段的代数应用题都会涉及到“工程问题”,然而,随着问题情境的不断变更,条件的不断变换,使得问题类型不再明朗,数量关系不再清晰,甚至错综复杂,难以理清,从而导致学生对应用类问题的学习出现明显的两极分化,致使不少学生对应用题看题生畏.出现以上情况的原因,除了应用题本身的综合性强,对学生的理解能力、生活阅历要求很高之外,还跟学段知识的局限有关,同时也与老师就题论题的教学方式有密切关系.本文案例选自于湘教版八上《15可化为一元一次方程的分式方程》第二课时.这节课的教学,笔者不再采用以往的教学模式:根据问题列出分式方程,求解、检验、回答;而是打破分式方程的限制,引导学生从不同的角度寻找数量关系,建立不同类型的方程(或方程组).下面以“工程问题”为例,谈谈应用题教学中的解题策略.1教学案例

21“一题多解”打破思维禁锢
波利亚指出:“掌握数学就是善于解题.”一题多解就是启发和引导学生从不同角度不同思路分析问题,从题目中尽可能的挖掘隐含条件,采用不同的方法不同的运算过程去解决问题,最终达到异曲同工的目的.在本案例中,笔者鼓励学生从不同角度思考,通过“一题多解”打破思维禁锢,突破解题瓶颈,形成开阔的解题路径.下面用方法导图展示解题路径.
方法导图:

22“一表多用”建立思维联系
应用题教学既是教师授课的难点,也是学生学习的难点.究其原因:(1)问题情境复杂;(2)数量关系隐蔽;(3)未知数选择灵活.这就需要学生首先要从复杂的问题情境中剔除无效的信息干扰,提炼有效的解题信息,这是一个去情景化实现数学抽象的过程.然后需要学生处理解题信息,将各量关系从文字语言向符号语言转换,实现隐性数量关系显性化的程序.在列方程的问题转换环节,学生往往可以借助线段图、表格等进行数量关系的分析.本案例采用表格将文字语言转换为图表语言,使得数量关系直观化、数量化,有效建立起多维度思考的桥梁.下面用列表导图展示解题思路.
列表导图:

2.3“多元歸一”揭示思维本质
“工程问题”的“一题多解”归根结底是对基本关系式:工作总量=工作时间×工作效率的变形使用,用其中的两个量表示第三个量;抓住其中的一个量建立方程,又可沿着:分开列方程和综合列方程展开;而综合列方程又可沿着:相等→和差→比例等角度展开,多种途径只因一个基本关系,可谓九九归一.“工程问题”的“解题策略”可归结为以下四步:第一步,明确问题类型;第二步,确定基本关系;第三步,写出关系列表;第四步,列出方程求解.整个流程形成了一个思维链.对于“工程问题”的解题策略和解题方法不仅仅局限于“工程问题”,与之关联的还有“行程问题”、“销售问题”、“利润问题”、“浓度问题”、“面积问题”等等,只要基本关系中涉及到三个量之间的积或商的关系均可.综上所述,由“工程问题”的解题研究引发的一系列思考,让我们不难发现应用题解题是一个系统工程,其中蕴含“一题多解”、“一法多用”、“多题归一”的数学思想,对培养学生的发射性思维和归纳演绎能力颇有益处.唯有认清问题的本质,才能突破解题的局限,长此以往方能去繁就简,优化解题方法.下面是对本案例研究的整体思维导图,让我们认清思维之间的联系.
案例研究思维导图:

作者简介涂爱玲(1976—),女,广西桂林人,中学高级教师,桂林市优秀教师,广西国培、区培优秀讲师.主要研究变式教学.撰写《中学数学变式教学问题设计与课例研究》,编写了两套变式教学教辅书,发表论文13篇,获奖论文30余篇.

