博采众长巧妙融合备出精彩
吴惠平+韩新正
【摘要】以“勾股定理”起始课为例,通过查阅文献资料,发现勾股定理起始课教学设计大致分为三类:以证明定理为主的教学设计、以探究发现定理为主的教学设计、以实验操作来发现定理的教学设计.分析不同设计的优缺点,博采众长,巧妙融合,从而备出一节基于“理解数学、理解学生、理解教学”的好课.
【关键词】勾股定理;文献资料;教学设计;实验操作
在“理解数学、理解学生、理解教学”的基础上备好一节课本是最好的备课方式,但由于教师理解能力的差异,以及对“三个理解”的认识程度不同,备课效果自然不可同日而语.那么,怎样才能备出一节好课呢?笔者认为,通过比对同一课时的文献资料,分析不同教案的优缺点,博采众长,巧妙融合,自然会备出一节好课.下面以“勾股定理”起始课为例,谈谈如何利用文献资料进行备课.供参考.
1常见教学设计
查阅近几年的文献资料,发现勾股定理起始课教学设计大致分为三类:以证明定理为主的教学设计、以探究发现定理为主的教学设计、以实验操作来发现定理的教学设计.现对这三种教学设计做客观分析.
1.1以证明定理为主的教学设计
章建跃博士在谈到勾股定理教数学时指出:“其一,勾股定理的发现具备偶然性;其二,毕达哥拉斯是大数学家,对数极其敏感,对“形”非常自动化地想到“数”,这是一般人做不到的……我觉得,不应该让学生去发现,重点应该放在让学生去证明这个定理.”[1]在这一观点的支撑下,一线教师中的许多实践者也取得了良好的教学效果.
课例1刘东升[2]先从一段BBC纪录片《数学的故事》展示古埃及人结绳绷成直角三角形导入新课,随即导入勾股定理的特例“如果作一个直角三角形,使得两直角边分别为3和4,你能否求出斜边的长?”在学生尝试无果后,教师指出有人曾经用拼图的方法求出该三角形的斜边长为5,接下来用拼图的方法予以计算.最后从特殊到一般用面积法(割补法)证明勾股定理.
分析教师设计以证明为主的教学思路,大致是基于以下几点思考:一是恰当安排讲授法,节约时间,采用教师讲授证明思路,学生跟进理解,是基于对学情的理解;二是勾股定理的发现具有偶然性,只有毕达哥拉斯这样的大数学家,才能从“形”非常自动地想到“数”,这是一般人做不到的,在课堂上有限的时间里让学生去发现该定理是不现实的,也是无法完成的任务.所以,该设计把时间重点分配在证明勾股定理和欣赏勾股定理文化上.从学习的角度看,这样的安排是有效的,是基于学情来考虑的,有利于学生学习数学知识,培养学生演绎推理的能力.
《义务教育阶段数学课程标准(2011版)》[3](以下简称标准)在课程基本理念中指出:学生学习应当是一个生动活泼的、主动的和富有个性的过程.除接受学习外,动手实践、自主探索与合作交流同样是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.显然,上述过程少了学生观察、实验、猜想的过程,而这却是数学教学的重要功能所在.事实上,发现一个定理的价值远远大于证明这个定理,从这个角度看,上述安排是不完美的.
1.2以探究发现定理为主的教学设计
特级教师卜以楼认为:研究一个定理,一般要从猜想——验证——证明这三个方面去把握,如果离开了猜想、发现定理这两个环节,那么培养学生的创新意識和实践能力就会在教学中打折.事实上,发现一个定理的价值远远大于证明这个定理.卜老师同时给出了基于上述思考的教学设计.
课例2卜以楼首先通过画两个直角三角形,引导学生发现直角三角形三边间有关系,然后顺势提出问题:既然直角三角形三边数量之间有一个等量关系,这个等量关系是什么呢[4]?接着,引导基础薄弱的学生在单位长度为1 cm的坐标纸上,理性地选择几个直角三角形去画一画、量一量,观察量出的数值,估计、猜想三边间的关系;引导基础较好的学生理性分析三边间的关系:a、b、c三边间关系可以是一次等量关系、二次等量关系,甚至是高次等量关系,根据三角形两边之和大于第三边否定三边间存在一次关系,然后探讨三边间的二次等量关系,先从特殊形式入手,首先猜想a2+b2=c2,经过验证发现猜想成立,再用“证伪”否定其它的二次关系,最后引导学生从a2、b2、c2这些“式结构”想到“边长分别为a、b、c的正方形面积”这个“形结构”,然后利用图形面积(割补法)来分析和解决问题.
分析首先,本课例关注学生四能培养,教学过程就是基于发现和提出问题,分析和解决问题的思路来设计的,教学过程就是引导学生思维的过程;其次,符合“猜想——验证——证明”的数学学习规律,过程严谨,丝丝入扣,数学味浓,注重学生思维能力和创新能力的培养.
但仔细分析其教学设计后发现,其课堂教学过于理想化,既要启发基础较差的学生画一画、量一量,观察量出的数值,估计、猜想三边间的关系,又要引导基础较好的学生理性分析三边间的关系,直至发现直角三角形三边的平方关系,还要引导学生证明勾股定理,复杂的教学过程可能会导致教学时间不够,文章展示的探究过程很难在现实的课堂中得以实现.另外,在引导基础较好的学生理性分析三边间关系的过程中,作者根据三角形两边之和大于第三边就可以否定三边间存在一次关系,这句话是有问题的,比如,边长分别为a=3、b=4、c=5的关系可以表述为a+b=75c这样的等量关系.对于a、b、c之间二次关系的三种形式的分类是可行的,但直接从特殊情况a2+b2=c2入手,是执果索因的结果,这和直接告知结论是一样的效果.
1.3以实验操作来发现定理的教学设计
苏科版数学教材主编董林伟先生指出:数学实验不是学生被动地接受课本上的或老师叙述的现成结论,而是学生从自己的数学现实出发,通过自己动手、动脑,用观察、模仿、实验、猜想等手段获得经验,逐步建构并发展自己的数学认知结构的活动过程[5].数学实验已成为数学教学中的一个重要方式.关于勾股定理的教学,数学实验大致有两种方法:测量法和计算法.
课例3测量法[6]:任党华引导学生从“直角三角形的角度特殊,会不会它的边在数量上也有特殊的关系呢?”开始思考,然后让学生动手画一个任意直角三角形,测量其三边长度,计算交流,接着学生展示所得数据及本组猜想,师生用几何画板演示,发现a2+b2=c2这一结论成立,再用拼图法证明结论,最后介绍有关勾股定理的数学史.
课例4计算法[7]:万广磊从展示2002年的数学大会的弦图开始,然后直接给出直角三角形和以该三角形三边向形外作三个正方形,通过填空的方式来计算三个正方形的面积,学生通过画一画、想一想、试一试、辨一辨来发现a2+b2=c2,再用实验的方法验证钝角三角形和锐角三角形不具备两短边的平方和等于最长边的平方,然后用拼图法证明勾股定理,最后介绍有关勾股定理的数学史.
分析这两个课例都是通过画一画、想一想、算一算来发现勾股定理的,动手实验的过程有利于培养学生的动手能力,获得研究问题的方法,积累活动经验.但课例3存在两点不足,一是学生画图、测量过程中无法保证图形的准确和数据的精确,不能为发现规律提供保证;二是学生从测量出的三边数据中,怎么会轻易发现三边的平方关系?课例4教师通过填空计算面积的方式已经把解题思路和盘托出,难点化为乌有,就像几何题中老师提前告知辅助线一样,是避开难点,而不是突破难点.罗增儒教授称以上教学为“虚假性情境发现”和“浅层次的情境发现”.
2勾股定理教学中需要突破的难点
通过上述课例的分析,我们不难发现在勾股定理的教学中回避不了几个难点:一是如何创设合适的情境,引导学生发现直角三角形三边间的平方关系?二是怎样引导学生从a2、b2、c2这些“式结构”想到“边长分别为a、b、c的正方形面积”这个“形结构”?三是选择探究教学,探究的时间较长,有时甚至不可控,需要时间成本;四是数学定理的呈现虽是美丽的,但发现的过程确是漫长和痛苦的,所以,课堂上定理的发现不能过于理想化,所谓还原数学家火热的思考,实在过于理想化,在短短的一节课内要完成一个定理的发现,必然要降低发现坡度,缩短发现时间,中间教师的引导甚至干预就必不可少.3吸收精华,改进教学设计
上述四个课例均有可取之处,在认真学习比对优劣的基础上,多方吸收各种教法中的精华,充分考虑勾股定理教学中需要突破的四大难点,经过认真整合,确定“从特殊到一般,经历猜想——验证——证明”这样的探究教学设计,在实际教学中取得了较好的效果.
3.1情境導入
在一个确定的三角形中,有确定的角的关系:①三角形内角和等于180°;②三角形外角和等于360°,那么,三角形三边间有确定的关系吗?
3.2探究发现
(1)从最特殊的三角形研究起,猜想直角三角形三边间关系
直角边长为1的等腰直角三角形的面积是多少?如果斜边用字母c表示,请用c表示三角形的面积.(S△ABC=12×1×1=12,S△ABC=12×c×12c=14c2,所以c2=2)

用同样的方法研究直角边长为2的等腰直角三角形,有什么发现?
(S△ABC=12×2×2=2,S△ABC=12×c×12c=14c2,所以c2=8).
依次研究直角边长分别为3、4的等腰直角三角形,会发现下面结论.
12+12=2=c2;22+22=8=c2;32+32=18=c2;42+42=32=c2(这里是需要教师干预和引导的)
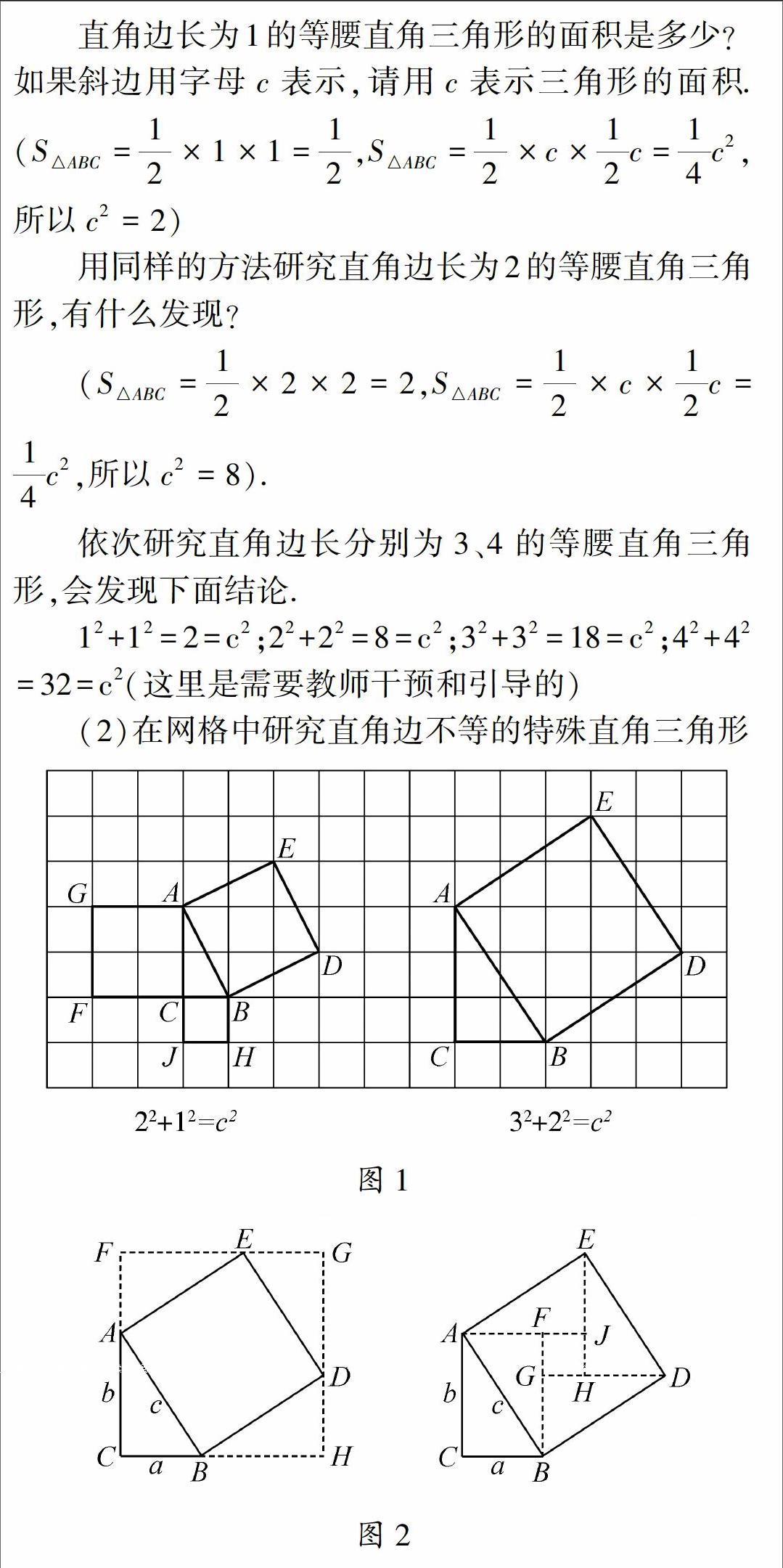
(2)在网格中研究直角边不等的特殊直角三角形图1
如果两直角边不等,上述猜想还成立吗?老师在黑板空白处画图分析,指出上面的方法行不通,能否借助格点正方形来发现呢?分析“式结构”,在上图(图1)中22=4,用四个正方形表示,12=1,用一个正方形表示,那么以斜边为边的正方形的面积是等于5吗?引导利用割补法研究(小学已经学过).
(3)几何画板验证猜想的结论
(4)不完全归纳法得出勾股定理
3.3定理证明与介绍
证明过程略.(图形割补见图2,证明思路见上面分析)
本设计在研究最简单的三角形时,学生是不可能想到运用面积来发现等腰直角三角形的三边关系的,这时教师直接引导先用两直角边求面积,再启发用斜边求面积,这个过程不自然,但确实没有更好的办法.所以,发现式教学不能不加干预,任由学生自由思考,正如佛赖登塔尔所说:“强调用发生的方法来教各种思想,并不意味着应该从它们产生的顺序来呈现它们,甚至不关闭所有的僵局,删除所有的弯路.”显然,这就是教师主导作用的意义所在.
综上所述,通过文献资料的研究,我们可以对相关内容的教学有清楚的认识,并在比较中去粗存精,获得比较合理的教学方法,这不失为一种行之有效的备课方式.
参考文献
[1]章建跃.理解数学内容本质提升思维教学水平[J].中学数学教学参考(中旬),2015(6):14-19.
[2]刘东升.基于HPM视角重构“勾股定理”起始课[J].教育研究与评论:课堂观察版(南京),2016(1):45-48.
[3]义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2011.
[4]卜以楼.基于四能的“勾股定理”教学创新设计[J].中学数学教学参考(中旬),2016(7):11-14.
[5]董林伟.初中数学实验教学的理论与实践[M].南京:江苏科学技术出版社,2013.
[6]任党华.勾股定理(第一课时)[J].中学数学教学参考(中旬),2015(6):12-13.
[7]万广磊.基于数学实验的勾股定理教学实践[J].中学数学(初中版),2015(4):34-37.
作者简介吴惠平( 1969—),女,高级教师,在省级以上刊物发表文章10多篇.主要从事课堂教学、教法和试题研究.

【摘要】以“勾股定理”起始课为例,通过查阅文献资料,发现勾股定理起始课教学设计大致分为三类:以证明定理为主的教学设计、以探究发现定理为主的教学设计、以实验操作来发现定理的教学设计.分析不同设计的优缺点,博采众长,巧妙融合,从而备出一节基于“理解数学、理解学生、理解教学”的好课.
【关键词】勾股定理;文献资料;教学设计;实验操作
在“理解数学、理解学生、理解教学”的基础上备好一节课本是最好的备课方式,但由于教师理解能力的差异,以及对“三个理解”的认识程度不同,备课效果自然不可同日而语.那么,怎样才能备出一节好课呢?笔者认为,通过比对同一课时的文献资料,分析不同教案的优缺点,博采众长,巧妙融合,自然会备出一节好课.下面以“勾股定理”起始课为例,谈谈如何利用文献资料进行备课.供参考.
1常见教学设计
查阅近几年的文献资料,发现勾股定理起始课教学设计大致分为三类:以证明定理为主的教学设计、以探究发现定理为主的教学设计、以实验操作来发现定理的教学设计.现对这三种教学设计做客观分析.
1.1以证明定理为主的教学设计
章建跃博士在谈到勾股定理教数学时指出:“其一,勾股定理的发现具备偶然性;其二,毕达哥拉斯是大数学家,对数极其敏感,对“形”非常自动化地想到“数”,这是一般人做不到的……我觉得,不应该让学生去发现,重点应该放在让学生去证明这个定理.”[1]在这一观点的支撑下,一线教师中的许多实践者也取得了良好的教学效果.
课例1刘东升[2]先从一段BBC纪录片《数学的故事》展示古埃及人结绳绷成直角三角形导入新课,随即导入勾股定理的特例“如果作一个直角三角形,使得两直角边分别为3和4,你能否求出斜边的长?”在学生尝试无果后,教师指出有人曾经用拼图的方法求出该三角形的斜边长为5,接下来用拼图的方法予以计算.最后从特殊到一般用面积法(割补法)证明勾股定理.
分析教师设计以证明为主的教学思路,大致是基于以下几点思考:一是恰当安排讲授法,节约时间,采用教师讲授证明思路,学生跟进理解,是基于对学情的理解;二是勾股定理的发现具有偶然性,只有毕达哥拉斯这样的大数学家,才能从“形”非常自动地想到“数”,这是一般人做不到的,在课堂上有限的时间里让学生去发现该定理是不现实的,也是无法完成的任务.所以,该设计把时间重点分配在证明勾股定理和欣赏勾股定理文化上.从学习的角度看,这样的安排是有效的,是基于学情来考虑的,有利于学生学习数学知识,培养学生演绎推理的能力.
《义务教育阶段数学课程标准(2011版)》[3](以下简称标准)在课程基本理念中指出:学生学习应当是一个生动活泼的、主动的和富有个性的过程.除接受学习外,动手实践、自主探索与合作交流同样是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.显然,上述过程少了学生观察、实验、猜想的过程,而这却是数学教学的重要功能所在.事实上,发现一个定理的价值远远大于证明这个定理,从这个角度看,上述安排是不完美的.
1.2以探究发现定理为主的教学设计
特级教师卜以楼认为:研究一个定理,一般要从猜想——验证——证明这三个方面去把握,如果离开了猜想、发现定理这两个环节,那么培养学生的创新意識和实践能力就会在教学中打折.事实上,发现一个定理的价值远远大于证明这个定理.卜老师同时给出了基于上述思考的教学设计.
课例2卜以楼首先通过画两个直角三角形,引导学生发现直角三角形三边间有关系,然后顺势提出问题:既然直角三角形三边数量之间有一个等量关系,这个等量关系是什么呢[4]?接着,引导基础薄弱的学生在单位长度为1 cm的坐标纸上,理性地选择几个直角三角形去画一画、量一量,观察量出的数值,估计、猜想三边间的关系;引导基础较好的学生理性分析三边间的关系:a、b、c三边间关系可以是一次等量关系、二次等量关系,甚至是高次等量关系,根据三角形两边之和大于第三边否定三边间存在一次关系,然后探讨三边间的二次等量关系,先从特殊形式入手,首先猜想a2+b2=c2,经过验证发现猜想成立,再用“证伪”否定其它的二次关系,最后引导学生从a2、b2、c2这些“式结构”想到“边长分别为a、b、c的正方形面积”这个“形结构”,然后利用图形面积(割补法)来分析和解决问题.
分析首先,本课例关注学生四能培养,教学过程就是基于发现和提出问题,分析和解决问题的思路来设计的,教学过程就是引导学生思维的过程;其次,符合“猜想——验证——证明”的数学学习规律,过程严谨,丝丝入扣,数学味浓,注重学生思维能力和创新能力的培养.
但仔细分析其教学设计后发现,其课堂教学过于理想化,既要启发基础较差的学生画一画、量一量,观察量出的数值,估计、猜想三边间的关系,又要引导基础较好的学生理性分析三边间的关系,直至发现直角三角形三边的平方关系,还要引导学生证明勾股定理,复杂的教学过程可能会导致教学时间不够,文章展示的探究过程很难在现实的课堂中得以实现.另外,在引导基础较好的学生理性分析三边间关系的过程中,作者根据三角形两边之和大于第三边就可以否定三边间存在一次关系,这句话是有问题的,比如,边长分别为a=3、b=4、c=5的关系可以表述为a+b=75c这样的等量关系.对于a、b、c之间二次关系的三种形式的分类是可行的,但直接从特殊情况a2+b2=c2入手,是执果索因的结果,这和直接告知结论是一样的效果.
1.3以实验操作来发现定理的教学设计
苏科版数学教材主编董林伟先生指出:数学实验不是学生被动地接受课本上的或老师叙述的现成结论,而是学生从自己的数学现实出发,通过自己动手、动脑,用观察、模仿、实验、猜想等手段获得经验,逐步建构并发展自己的数学认知结构的活动过程[5].数学实验已成为数学教学中的一个重要方式.关于勾股定理的教学,数学实验大致有两种方法:测量法和计算法.
课例3测量法[6]:任党华引导学生从“直角三角形的角度特殊,会不会它的边在数量上也有特殊的关系呢?”开始思考,然后让学生动手画一个任意直角三角形,测量其三边长度,计算交流,接着学生展示所得数据及本组猜想,师生用几何画板演示,发现a2+b2=c2这一结论成立,再用拼图法证明结论,最后介绍有关勾股定理的数学史.
课例4计算法[7]:万广磊从展示2002年的数学大会的弦图开始,然后直接给出直角三角形和以该三角形三边向形外作三个正方形,通过填空的方式来计算三个正方形的面积,学生通过画一画、想一想、试一试、辨一辨来发现a2+b2=c2,再用实验的方法验证钝角三角形和锐角三角形不具备两短边的平方和等于最长边的平方,然后用拼图法证明勾股定理,最后介绍有关勾股定理的数学史.
分析这两个课例都是通过画一画、想一想、算一算来发现勾股定理的,动手实验的过程有利于培养学生的动手能力,获得研究问题的方法,积累活动经验.但课例3存在两点不足,一是学生画图、测量过程中无法保证图形的准确和数据的精确,不能为发现规律提供保证;二是学生从测量出的三边数据中,怎么会轻易发现三边的平方关系?课例4教师通过填空计算面积的方式已经把解题思路和盘托出,难点化为乌有,就像几何题中老师提前告知辅助线一样,是避开难点,而不是突破难点.罗增儒教授称以上教学为“虚假性情境发现”和“浅层次的情境发现”.
2勾股定理教学中需要突破的难点
通过上述课例的分析,我们不难发现在勾股定理的教学中回避不了几个难点:一是如何创设合适的情境,引导学生发现直角三角形三边间的平方关系?二是怎样引导学生从a2、b2、c2这些“式结构”想到“边长分别为a、b、c的正方形面积”这个“形结构”?三是选择探究教学,探究的时间较长,有时甚至不可控,需要时间成本;四是数学定理的呈现虽是美丽的,但发现的过程确是漫长和痛苦的,所以,课堂上定理的发现不能过于理想化,所谓还原数学家火热的思考,实在过于理想化,在短短的一节课内要完成一个定理的发现,必然要降低发现坡度,缩短发现时间,中间教师的引导甚至干预就必不可少.3吸收精华,改进教学设计
上述四个课例均有可取之处,在认真学习比对优劣的基础上,多方吸收各种教法中的精华,充分考虑勾股定理教学中需要突破的四大难点,经过认真整合,确定“从特殊到一般,经历猜想——验证——证明”这样的探究教学设计,在实际教学中取得了较好的效果.
3.1情境導入
在一个确定的三角形中,有确定的角的关系:①三角形内角和等于180°;②三角形外角和等于360°,那么,三角形三边间有确定的关系吗?
3.2探究发现
(1)从最特殊的三角形研究起,猜想直角三角形三边间关系
直角边长为1的等腰直角三角形的面积是多少?如果斜边用字母c表示,请用c表示三角形的面积.(S△ABC=12×1×1=12,S△ABC=12×c×12c=14c2,所以c2=2)

用同样的方法研究直角边长为2的等腰直角三角形,有什么发现?
(S△ABC=12×2×2=2,S△ABC=12×c×12c=14c2,所以c2=8).
依次研究直角边长分别为3、4的等腰直角三角形,会发现下面结论.
12+12=2=c2;22+22=8=c2;32+32=18=c2;42+42=32=c2(这里是需要教师干预和引导的)
(2)在网格中研究直角边不等的特殊直角三角形图1
如果两直角边不等,上述猜想还成立吗?老师在黑板空白处画图分析,指出上面的方法行不通,能否借助格点正方形来发现呢?分析“式结构”,在上图(图1)中22=4,用四个正方形表示,12=1,用一个正方形表示,那么以斜边为边的正方形的面积是等于5吗?引导利用割补法研究(小学已经学过).
(3)几何画板验证猜想的结论
(4)不完全归纳法得出勾股定理
3.3定理证明与介绍
证明过程略.(图形割补见图2,证明思路见上面分析)
本设计在研究最简单的三角形时,学生是不可能想到运用面积来发现等腰直角三角形的三边关系的,这时教师直接引导先用两直角边求面积,再启发用斜边求面积,这个过程不自然,但确实没有更好的办法.所以,发现式教学不能不加干预,任由学生自由思考,正如佛赖登塔尔所说:“强调用发生的方法来教各种思想,并不意味着应该从它们产生的顺序来呈现它们,甚至不关闭所有的僵局,删除所有的弯路.”显然,这就是教师主导作用的意义所在.
综上所述,通过文献资料的研究,我们可以对相关内容的教学有清楚的认识,并在比较中去粗存精,获得比较合理的教学方法,这不失为一种行之有效的备课方式.
参考文献
[1]章建跃.理解数学内容本质提升思维教学水平[J].中学数学教学参考(中旬),2015(6):14-19.
[2]刘东升.基于HPM视角重构“勾股定理”起始课[J].教育研究与评论:课堂观察版(南京),2016(1):45-48.
[3]义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2011.
[4]卜以楼.基于四能的“勾股定理”教学创新设计[J].中学数学教学参考(中旬),2016(7):11-14.
[5]董林伟.初中数学实验教学的理论与实践[M].南京:江苏科学技术出版社,2013.
[6]任党华.勾股定理(第一课时)[J].中学数学教学参考(中旬),2015(6):12-13.
[7]万广磊.基于数学实验的勾股定理教学实践[J].中学数学(初中版),2015(4):34-37.
作者简介吴惠平( 1969—),女,高级教师,在省级以上刊物发表文章10多篇.主要从事课堂教学、教法和试题研究.

