初中数学典型几何模型

    赵丽红

    

    

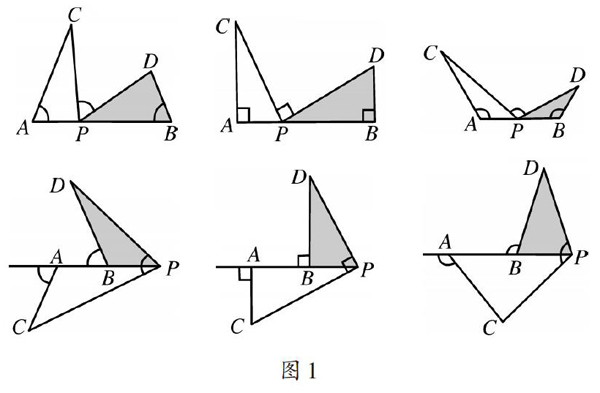
    [摘???要]中考数学试题一般以典型代数模型、几何模型为依托，熟悉和掌握初中数学的一些代数与几何模型的使用方法，对解答中高难度的试题将有很大的帮助.“一线三等角”模型是典型的几何模型.此模型又可分为锐角一线三等角、直角一线三等角和钝角一线三等角.“一线三等角”模型一般不单独出现，它通常与其他特殊图形结合，如等腰三角形、等边三角形、矩形、正方形，以及与翻折、坐标系结合等，从而考查这些图形的性质.

    [关键词]一线三等角模型;几何模型;初中数学

    [中图分类号]????G633.6????????[文献标识码]????A????????[文章编号]????1674-6058（2019）35-0037-02

    “一线三等角”是指三个相等的角的顶点在同一直线上，其中两个角的一边与该直线重合，第三个角的两边均不与直线重合，这样会形成一组全等或相似三角形.根据等角的度数，此模型又可分为锐角一线三等角、直角一线三等角和钝角一线三等角，其基本图形如图1所示，它们均有△ACP∽△BPD.

    “一线三等角”模型一般不单独出现，它通常与其他特殊图形结合，如等腰三角形、等边三角形、矩形、正方形，以及与翻折、坐标系结合等，从而考查这些图形的性质.以下就是考试中常出现的试题形式.

    一、等腰三角形中的“一线三等角”

    因为等腰三角形有“两底角相等”的性质，所以“一线三等角”在等腰三角形中出现频率最高，通常利用三角形外角的性质得到另一组等角，然后利用“有两个角分别对应相等的两个三角形相似”得证相似三角形.

    [例1]如图2，在△ABC中，AC=BC，点D是线段AB上一动点，∠EDF绕点D旋转，在旋转过程中始终保持∠A=∠EDF，射线DE与边AC交于点M，射线DF与边BC交于点N，连接MN.

    （1）找出图中的一对相似三角形，并证明你的结论;

    （2）如图3，在上述条件下，当点D运动到AB的中点时，求证：在∠EDF绕点D旋转过程中，点D到线段MN的距离为定值.

    解析：（1）[△ADM∽△BND].理由：∵AC=BC，∴∠A=∠B，∵∠A+∠AMD?=∠EDF+∠BDN，∵∠A=∠EDF，?∴∠AMD=∠BDN，∴△ADM∽△BND;

    （2）如图4，作DG⊥MN于G，DH⊥AM于H，由（1）得，△ADM?∽△BND，∴[AMBD=DMDN]，∵AD?=?BD，∴[AMAD=DMDN]，又∠A∠EDF，∴△ADM∽△DNM，∴∠AMD=∠NMD，又∵DG⊥MN，DH⊥AM，∴DG=DH，即在∠EDF绕点D旋转过程中，点D到线段MN的距离为定值.

    评注：对于等腰三角形中的“一线三等角”，当第三个角的顶点恰好在底边中点时，图中中间的三角形与两边的两个三角形也相似，可称之为“中点型一线三等角”.

    二、等边三角形中的“一线三等角”

    等边三角形的“一线三等角中，更多关注的是全等三角形，且第三等角位置变化时，研究有关线段不变的数量与位置关系.

    [例2]如图5所示，已知：△ABC为等边三角形，D为直线BC上一点，以AD为边作等边△ADE.

    （1）当点D在线段BC上时，求证：BD=CE，AB∥CE;

    （2）若点D在CB的延长线上，上述结论是否成立？若成立，补画图形并证明，若不成立，说明理由.

    解析：（1）∵△ABC和△ADE都是等边三角形，∴AB=AC?=?BC，AD?=?AE，∠BAC?=∠DAE?=?60°.∴∠BAC-∠CAD=∠DAE-∠CAD，即∠BAD=∠CAE.在△ABD和△ACE中，[AB=AC?，∠BAD=∠CAEAD=AE?，]，

    ∴△ABD?≌△ACE（SAS），∴BD=CE，∠ACE=∠B=60°，∴∠ECF=60°，∴∠ECF=∠B，∴AB∥CE;

    （2）补画图形如图6所示.上述结论成立.理由如下：∵△ABC和△ADE都是等边三角形，∴AB?=?AC?=?BC，?AD?=?AE，∠BAC?=∠DAE?=?60°.∴∠BAC+∠CAD?=?∠DAE+∠CAD，∴∠BAD=∠CAE，在△ABD和△ACE中，[AB=AC?，∠BAD=∠CAEAD=AE?，]，

    ∴△ABD?≌△ACE（SAS），∴BD=CE，∠ACE?=∠B?=?60°，∴∠ECF?=?60°，∴∠ECF=∠B，∴AB∥CE?.

    评注：本题第（2）小题是“一线三等角”的变形，但证明的方法仍与前面相同，甚至第（2）小题证明过程字母都没改变，可見证明思路完全相同，这是拓展延伸问题惯用的手法.

    三、矩形折叠中的“一线三等角”

    矩形折叠中的“一线三等角”常表现为“直角一线三等角”，因为矩形的每个角都是直角，把矩形的一个角折叠，当它的直角顶点落在矩形一边上时，就会形成“一线三等角”的模型，得到两个相似三角形，然后利用对应边成比例求得有关线段的长.

    [例3]如图7，在矩形ABCD中，AB=1，BC=a，点E在边BC上，且BE=[35a].连接AE，将△ABE沿AE折叠，若点B的对应点B′落在矩形ABCD的边上，则a的值为????????????????.

    解析：①?当点B′落在AD边上时，如图8.∵四边形ABCD是矩形，∴∠BAD?=?∠B?=?90°，∵将△ABE沿AE折叠，点B的对应点B′落在AD边上，∴∠BAE?=?∠B′AE?=?[12]∠BAD?=?45°，∴AB?=?BE，∴[35]?a=1，∴a?=?[53];

    ②当点B′落在CD边上时，如图9.∵四边形ABCD是矩形，∴∠BAD=∠B=∠C=∠D=90°，AD=BC=a.∵将△ABE沿AE折叠，点B的对应点B′落在CD边上，∴∠B=∠AB′E=90°，AB=AB′=1，EB=EB′=?[35]?a，∴DB′=[B′A2-AD2]=[1-a2]，EC=BC-BE=a-[35]?a=[25]?a.在△ADB′与△B′CE中，[∠B′AD=∠EB′C=90°-∠AB′D，∠D=∠C=90°，]∴△ADB′∽△B′CE，∴[DB'CE]=[AB'B'E]，即[1-a225a]=[135a]，解得a1=[53]，a2=0（舍去）.综上，所求a的值为[53]或[53].

    综上可知，在解题时，要学会从复杂图形中提取出基本图形，灵活地运用基本结论思考拓展，通过知识间的串联，找出一些通性通法，从而有效解决问题.

    （特约编辑????安???平）