积极开展探究活动,提高学生数学能力
李树臣?だ羁吮Κオ?
【摘要】数学教育的根本目的在于提高学生的数学素养,而数学能力是数学素养的核心构成要素.数学探究活动是以学生能主动发现问题、提出问题、分析问题以及解决问题为目的的学习活动,这种学习活动有三种形式,分为四个过程.开展探究活动的关键在于设计有价值的问题,学生在问题引导下大胆进行探究,在探究过程中,教师要给学生留出足够的探究时间并给予必要的指导.
【关键词】数学探究;设计问题;探究发现;问题解决
《义务教育数学课程标准》(2011年版)(以下简称《课标(2011年版)》)指出:“数学教育既要使学生掌握现代生活和学习中所需的数学知识与技能,更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用.”[1]数学教育的根本目的是提高学生的数学素养,而数学能力是数学素养的核心构成要素.在教学中,结合具体内容,引导学生积极开展探究活动是培养学生数学能力的主要途径.1对数学探究的再认识
数学探究是指学生在教师的启发诱导下,以独立自主学习和合作讨论为前提,以解决问题为探究内容,以学生能主动发现问题、提出问题、分析问题、解决问题为目的的学习活动.
1.1探究活动的基本形式
数学学习本身就是一个师生共同探究的过程,数学探究活动的主体是学生,从这个意义上讲,学生的探究活动可分为三种基本形式[2]:
(1)独立探究
独立探究是指学生个体对所探究的问题进行独立思考与探究,是探究活动的最基本形式.教学中对于一些较为简单的数学基础知识,我们可以通过创设一定的问题情境,引导学生独立思考与探究,在独立探究的过程中自主发现有关知识,完成对《课标(2011年版)》界定的数学基础知识的学习.
(2)合作探究
合作探究是在合作学习的前提下进行的,是指学习小组内学生之间对探究问题共同进行探究活动,合作探究一般是在学生已经经过独立探究活动,但探究的问题仍得不到很好解决的前提下所采取的一种探究活动方式.
(3)引导探究
引导探究是在教师引导下学生对问题进行的研究,引导探究一般是在学生已经经过独立探究与合作探究活动,但绝大多数学生对所探究的问题仍感到无能为力或束手无策时所采取的一种探究方式.引导探究活动的方式是在学生独立探究与合作探究的基础上进行的.
由于探究问题的难度不同、加上学生的探究能力也存在一定的差异,所以选择探究活动的方式也往往有所不同.在课堂教学中,不管采用哪种探究方式,都必须遵循“教师要发挥主导作用,处理好讲授与学生自主学习的关系,引导学生独立思考、主动探索、合作交流,使学生理解和掌握基本的数学知识与技能、体会和运用数学思想与方法,获得基本的数学活动经验”[1]的《课标(2011年版)》理念.
我们选择探究活动方式的原则是:能由学生独立探究完成的就不采用合作探究;能由学生合作探究完成的就不采用引导探究.在三种探究形式中,独立探究是前提,合作探究、引导探究是独立探究的补充和发展.数学探究活动的过程如图1所示[2]:图1
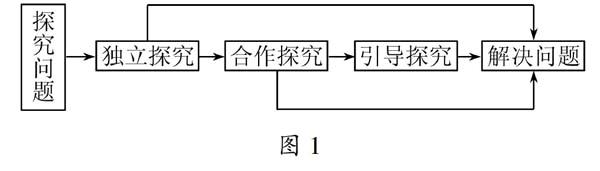
1.2探究活动的一般过程
一个完整的探究活动一般分为四个过程:
(1)提出问题
教师通过研究教学内容和分析学生的接受能力,精心设计一系列的问题(不是一个问题,而是由几个问题组成的“问题串”),呈现给学生.
(2)拟定探究方案
学生根据教师提出的问题,确定探究方向,拟定探究计划.当然这个方案的拟定很多情况下需要教师指导.
(3)实施探究
这是探究活动的关键环节.学生围绕教师所提出的问题及确定的探究方案,着手收集与问题相关的信息,进行一系列的活动(如阅读教材、独立思考、分析判断、实验操作,推理验算、归纳总结、相互交流等),在经历数学活动的过程中,进行自主探究学习,并且经历发现问题、提出问题、分析问题和解决问题的过程.
(4)形成结论
学生在探究的基础上,根据逻辑关系和推理,找到问题的症结所在,对其中的因果关系形成自己的解释.当然,结论的归纳、总结往往需要教师的点拨和引导.
学生开展探究活动不一定严格按照这四个过程(如不一定要制定探究方案)进行,但第一个和第三个过程是不可缺少的.笔者认为,只要学生在问题的引导下能积极开展观察、思考、计算、推理、讨论等活动自主获得结论,就算经历了一个很有意义的探究活动.数学教学中长期坚持这样的练习,学生的综合数学能力将会得到提高和发展.
1.3开展探究活动的教育教学价值
澳大利亚一个物理教师曾经说过,他第一个十年在教物理,第二个十年在引导学生探究物理,第三个十年在为进行探究的学生提供支持和帮助.这位物理老师的话,很值得我们数学老师思考与借鉴.在数学教学中引导学生开展探究活动的意义主要表现在以下三个方面:
(1)加深对数学知识的理解
对于任何知识(当然包括数学知识),如果是学生通过探究活动自己发现的,将比教师直接讲授印象深刻,记忆长远.因为学生对通过探究得到的知识不仅“知其然”,而且还能“知其所以然”,从而达到对数学知识的深层次理解和掌握.
(2)学会研究问题的一般方法
学生通过探究获得知识的同时,将会经历一系列的活动,在经历这些活动的过程中,可积累研究问题的经验,掌握研究问题的一般方法,这对于他们继续学习直至将来的工作都具有重要的意义.
(3)有利于培养学生的创新意识
《课标(2011年版)》倡导培养学生的“创新意识”,这种意识形成的前提是要具备一定的创新精神和创新能力.学生通过开展探究活动,能体验获得成功的乐趣,锻炼克服困难的意志,建立自信心,能形成科学的态度和习惯,形成实事求是、精益求精、客观公正、敢于创新的精神,这些都是学生创新意识形成过程中不可或缺的因素,也是我们进行数学教育教学的崇高目标.2精心设计探究问题
开展探究活动,关键是设计好的问题,这样的“问题”不同于一般的数学题.罗增儒教授认为,这样的数学题具有一些基本的特征,其中之一是“探究性”,即对于这样的问题,我们“没有现成的直接方法、程序或算法”,学生不能简单地模仿现成的公式或沿用常规的解题套路,需要进行观察、实验、猜测、计算、推理、验证等探究活动才能解决[3].设计这样的问题,需要教师在备课中多下功夫,因此,许多老师感觉不如用传统的讲授法省时省力,下面的考题对于倡导实施探究教学具有“指挥棒”的作用.
2.1原题呈现
问题提出(2016年青岛市中考数学第23题)如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形(a×b的矩形指边长分别为a,b的矩形)?
问题探究我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一
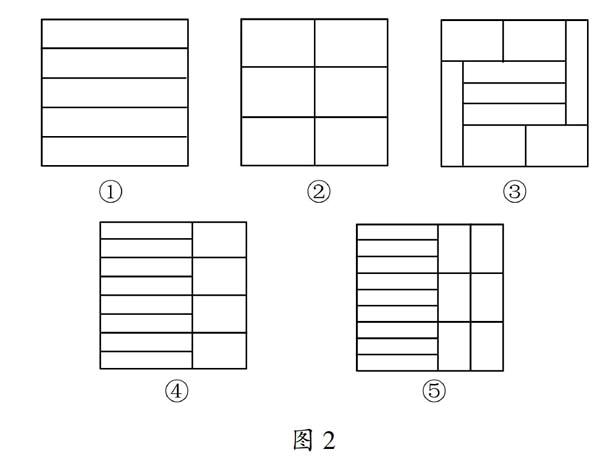
如图2①,当n=5时,可将正方形分割为五个1×5的矩形.
如图2②,当n=6时,可将正方形分割为六个2×3的矩形.
如图2③,当n=7时,可将正方形分割为五个1×5的矩形和四个2×3的矩形.
如图2④,当n=8时,可将正方形分割为八个1×5的矩形和四个2×3的矩形.
如图2⑤,当n=9时,可将正方形分割为九个1×5的矩形和六个2×3的矩形.
探究二
当n=10,11,12,13,14时,分别将正方形按下列方式分割(图3):
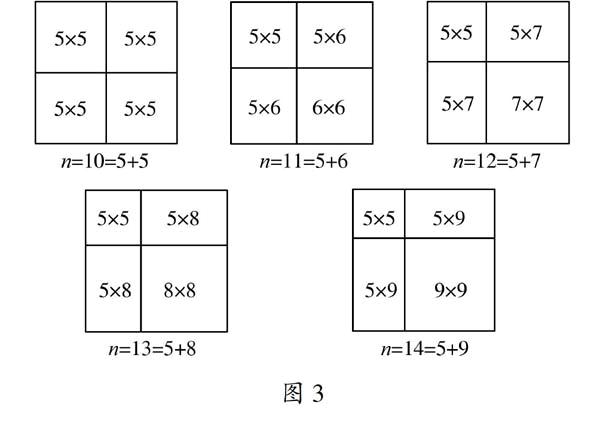
所以,当n=10,11,12,13,14时,均可将正方形分割为一个5×5的正方形、一个
(n-5)×(n-5)的正方形和两个5×(n-5)的矩形.显然,5×5的正方形和5×(n-5)的矩形均可分割为1×5的矩形,而(n-5)×(n-5)的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1×5或2×3的矩形.
探究三
当n=15,16,17,18,19时,分别将正方形按下列方式分割(图4):
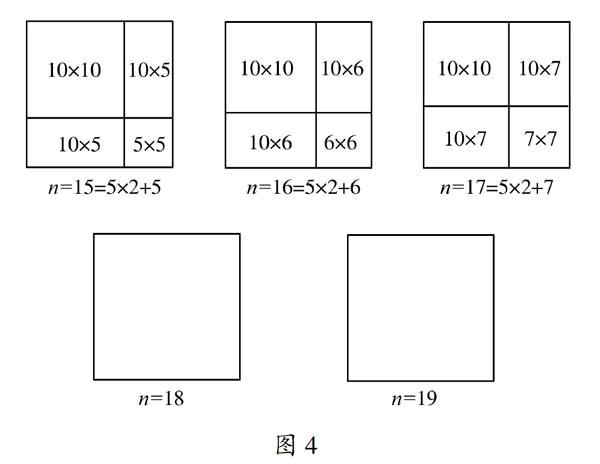
请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
由上图,当n=15,16,17,18,19时,均可将正方形分割为一个10×10的正方形、一个(n-10)×(n-10)的正方形和两个10×(n-10)的矩形.显然,10×10的正方形和10×(n-10)的矩形均可分割为1×5的矩形,而(n-10)×(n-10)的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1×5或2×3的矩形.
问题解决如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用如何将边长为61的正方形分割为一些1×5或2×3的矩形?(只需按照探究三的方法画出分割示意图即可)
2.2分析解答
本题分为“问题提出——问题探究——问题解决——实际应用”四个部分,题目叙述篇幅较长,需要学生有较强的阅读理解能力.
第一部分提出“问题”:如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形?这是核心目的,通过后面的一系列探究活动,最终得到计算的通解(模型):可分割成一个5m×5m的正方形,一个(n-5m)×(n-5m)的正方形和两个5m×(n-5m)的矩形.
为了引导学生解决这个问题,题目给出了第二部分(问题探究),这部分是针对核心问题而精心设计的,它从n的最小值出发,采用逐渐增大的方法,由三个探究活动构成:
第一个,令n≥5,当n=5,6,7,8,9时,直接给出了将正方形分割的情况(如图2),这是第二部分整个探究活动的关键和突破口,有了这个探究活动作为基础,后面的活动就有了方向和思路.
第二个,直接给出当n=10,11,12,13,14时将正方形分割的情况(如图3)
这两个探究活动是第二部分的关键,相当于教科书中的“例题”,目的是让学生探究分割一类图形问题的通用方法,发现规律,积累探究经验.
第三个,原题直接给出n=15,16,17时的分割结果(图4的前三个图),让学生仿照这三个分割结果,给出当n=18,19时的分割结果.对于这个问题只要学生真正领悟了前两个探究活动的“实质”,仿照其方法,就能画出当n=18,19时的分割图(如图5).
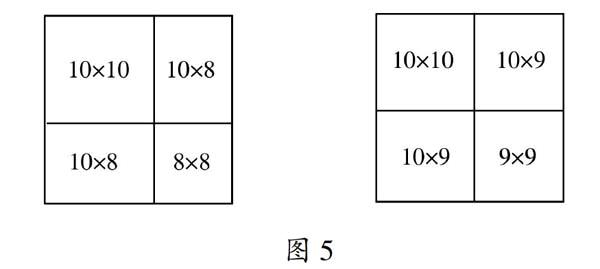
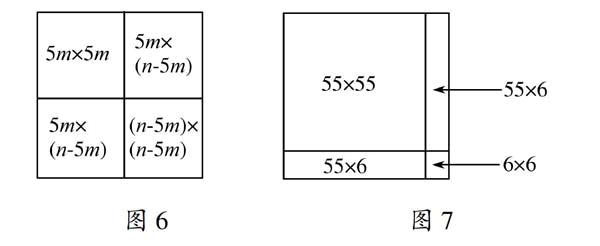
第三部分问题解决,回到本题的核心,当正方形的边长为n(n≥5,且n为整数)时,按图6的方式均可将正方形分割为一个5m×5m的正方形,一个(n-5m)×(n-5m)的正方形和两个5m×(n-5m)的矩形.显然5m×5m的正方形和5m×(n-5m)的矩形均可分割为1×5的矩形,而(n-5m)×(n-5m)的正方形又是边长分别为5,6,7,8,9的正方形,用探究的方法可分割为一些1×5或2×3的矩形.
第四部分实际应用的答案如图7所示.图6图7
【摘要】数学教育的根本目的在于提高学生的数学素养,而数学能力是数学素养的核心构成要素.数学探究活动是以学生能主动发现问题、提出问题、分析问题以及解决问题为目的的学习活动,这种学习活动有三种形式,分为四个过程.开展探究活动的关键在于设计有价值的问题,学生在问题引导下大胆进行探究,在探究过程中,教师要给学生留出足够的探究时间并给予必要的指导.
【关键词】数学探究;设计问题;探究发现;问题解决
《义务教育数学课程标准》(2011年版)(以下简称《课标(2011年版)》)指出:“数学教育既要使学生掌握现代生活和学习中所需的数学知识与技能,更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用.”[1]数学教育的根本目的是提高学生的数学素养,而数学能力是数学素养的核心构成要素.在教学中,结合具体内容,引导学生积极开展探究活动是培养学生数学能力的主要途径.1对数学探究的再认识
数学探究是指学生在教师的启发诱导下,以独立自主学习和合作讨论为前提,以解决问题为探究内容,以学生能主动发现问题、提出问题、分析问题、解决问题为目的的学习活动.
1.1探究活动的基本形式
数学学习本身就是一个师生共同探究的过程,数学探究活动的主体是学生,从这个意义上讲,学生的探究活动可分为三种基本形式[2]:
(1)独立探究
独立探究是指学生个体对所探究的问题进行独立思考与探究,是探究活动的最基本形式.教学中对于一些较为简单的数学基础知识,我们可以通过创设一定的问题情境,引导学生独立思考与探究,在独立探究的过程中自主发现有关知识,完成对《课标(2011年版)》界定的数学基础知识的学习.
(2)合作探究
合作探究是在合作学习的前提下进行的,是指学习小组内学生之间对探究问题共同进行探究活动,合作探究一般是在学生已经经过独立探究活动,但探究的问题仍得不到很好解决的前提下所采取的一种探究活动方式.
(3)引导探究
引导探究是在教师引导下学生对问题进行的研究,引导探究一般是在学生已经经过独立探究与合作探究活动,但绝大多数学生对所探究的问题仍感到无能为力或束手无策时所采取的一种探究方式.引导探究活动的方式是在学生独立探究与合作探究的基础上进行的.
由于探究问题的难度不同、加上学生的探究能力也存在一定的差异,所以选择探究活动的方式也往往有所不同.在课堂教学中,不管采用哪种探究方式,都必须遵循“教师要发挥主导作用,处理好讲授与学生自主学习的关系,引导学生独立思考、主动探索、合作交流,使学生理解和掌握基本的数学知识与技能、体会和运用数学思想与方法,获得基本的数学活动经验”[1]的《课标(2011年版)》理念.
我们选择探究活动方式的原则是:能由学生独立探究完成的就不采用合作探究;能由学生合作探究完成的就不采用引导探究.在三种探究形式中,独立探究是前提,合作探究、引导探究是独立探究的补充和发展.数学探究活动的过程如图1所示[2]:图1

1.2探究活动的一般过程
一个完整的探究活动一般分为四个过程:
(1)提出问题
教师通过研究教学内容和分析学生的接受能力,精心设计一系列的问题(不是一个问题,而是由几个问题组成的“问题串”),呈现给学生.
(2)拟定探究方案
学生根据教师提出的问题,确定探究方向,拟定探究计划.当然这个方案的拟定很多情况下需要教师指导.
(3)实施探究
这是探究活动的关键环节.学生围绕教师所提出的问题及确定的探究方案,着手收集与问题相关的信息,进行一系列的活动(如阅读教材、独立思考、分析判断、实验操作,推理验算、归纳总结、相互交流等),在经历数学活动的过程中,进行自主探究学习,并且经历发现问题、提出问题、分析问题和解决问题的过程.
(4)形成结论
学生在探究的基础上,根据逻辑关系和推理,找到问题的症结所在,对其中的因果关系形成自己的解释.当然,结论的归纳、总结往往需要教师的点拨和引导.
学生开展探究活动不一定严格按照这四个过程(如不一定要制定探究方案)进行,但第一个和第三个过程是不可缺少的.笔者认为,只要学生在问题的引导下能积极开展观察、思考、计算、推理、讨论等活动自主获得结论,就算经历了一个很有意义的探究活动.数学教学中长期坚持这样的练习,学生的综合数学能力将会得到提高和发展.
1.3开展探究活动的教育教学价值
澳大利亚一个物理教师曾经说过,他第一个十年在教物理,第二个十年在引导学生探究物理,第三个十年在为进行探究的学生提供支持和帮助.这位物理老师的话,很值得我们数学老师思考与借鉴.在数学教学中引导学生开展探究活动的意义主要表现在以下三个方面:
(1)加深对数学知识的理解
对于任何知识(当然包括数学知识),如果是学生通过探究活动自己发现的,将比教师直接讲授印象深刻,记忆长远.因为学生对通过探究得到的知识不仅“知其然”,而且还能“知其所以然”,从而达到对数学知识的深层次理解和掌握.
(2)学会研究问题的一般方法
学生通过探究获得知识的同时,将会经历一系列的活动,在经历这些活动的过程中,可积累研究问题的经验,掌握研究问题的一般方法,这对于他们继续学习直至将来的工作都具有重要的意义.
(3)有利于培养学生的创新意识
《课标(2011年版)》倡导培养学生的“创新意识”,这种意识形成的前提是要具备一定的创新精神和创新能力.学生通过开展探究活动,能体验获得成功的乐趣,锻炼克服困难的意志,建立自信心,能形成科学的态度和习惯,形成实事求是、精益求精、客观公正、敢于创新的精神,这些都是学生创新意识形成过程中不可或缺的因素,也是我们进行数学教育教学的崇高目标.2精心设计探究问题
开展探究活动,关键是设计好的问题,这样的“问题”不同于一般的数学题.罗增儒教授认为,这样的数学题具有一些基本的特征,其中之一是“探究性”,即对于这样的问题,我们“没有现成的直接方法、程序或算法”,学生不能简单地模仿现成的公式或沿用常规的解题套路,需要进行观察、实验、猜测、计算、推理、验证等探究活动才能解决[3].设计这样的问题,需要教师在备课中多下功夫,因此,许多老师感觉不如用传统的讲授法省时省力,下面的考题对于倡导实施探究教学具有“指挥棒”的作用.
2.1原题呈现
问题提出(2016年青岛市中考数学第23题)如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形(a×b的矩形指边长分别为a,b的矩形)?
问题探究我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一
如图2①,当n=5时,可将正方形分割为五个1×5的矩形.
如图2②,当n=6时,可将正方形分割为六个2×3的矩形.
如图2③,当n=7时,可将正方形分割为五个1×5的矩形和四个2×3的矩形.
如图2④,当n=8时,可将正方形分割为八个1×5的矩形和四个2×3的矩形.
如图2⑤,当n=9时,可将正方形分割为九个1×5的矩形和六个2×3的矩形.

探究二
当n=10,11,12,13,14时,分别将正方形按下列方式分割(图3):

所以,当n=10,11,12,13,14时,均可将正方形分割为一个5×5的正方形、一个
(n-5)×(n-5)的正方形和两个5×(n-5)的矩形.显然,5×5的正方形和5×(n-5)的矩形均可分割为1×5的矩形,而(n-5)×(n-5)的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1×5或2×3的矩形.
探究三
当n=15,16,17,18,19时,分别将正方形按下列方式分割(图4):

请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
由上图,当n=15,16,17,18,19时,均可将正方形分割为一个10×10的正方形、一个(n-10)×(n-10)的正方形和两个10×(n-10)的矩形.显然,10×10的正方形和10×(n-10)的矩形均可分割为1×5的矩形,而(n-10)×(n-10)的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些1×5或2×3的矩形.
问题解决如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用如何将边长为61的正方形分割为一些1×5或2×3的矩形?(只需按照探究三的方法画出分割示意图即可)
2.2分析解答
本题分为“问题提出——问题探究——问题解决——实际应用”四个部分,题目叙述篇幅较长,需要学生有较强的阅读理解能力.
第一部分提出“问题”:如何将边长为n(n≥5,且n为整数)的正方形分割为一些1×5或2×3的矩形?这是核心目的,通过后面的一系列探究活动,最终得到计算的通解(模型):可分割成一个5m×5m的正方形,一个(n-5m)×(n-5m)的正方形和两个5m×(n-5m)的矩形.
为了引导学生解决这个问题,题目给出了第二部分(问题探究),这部分是针对核心问题而精心设计的,它从n的最小值出发,采用逐渐增大的方法,由三个探究活动构成:
第一个,令n≥5,当n=5,6,7,8,9时,直接给出了将正方形分割的情况(如图2),这是第二部分整个探究活动的关键和突破口,有了这个探究活动作为基础,后面的活动就有了方向和思路.
第二个,直接给出当n=10,11,12,13,14时将正方形分割的情况(如图3)
这两个探究活动是第二部分的关键,相当于教科书中的“例题”,目的是让学生探究分割一类图形问题的通用方法,发现规律,积累探究经验.
第三个,原题直接给出n=15,16,17时的分割结果(图4的前三个图),让学生仿照这三个分割结果,给出当n=18,19时的分割结果.对于这个问题只要学生真正领悟了前两个探究活动的“实质”,仿照其方法,就能画出当n=18,19时的分割图(如图5).

第三部分问题解决,回到本题的核心,当正方形的边长为n(n≥5,且n为整数)时,按图6的方式均可将正方形分割为一个5m×5m的正方形,一个(n-5m)×(n-5m)的正方形和两个5m×(n-5m)的矩形.显然5m×5m的正方形和5m×(n-5m)的矩形均可分割为1×5的矩形,而(n-5m)×(n-5m)的正方形又是边长分别为5,6,7,8,9的正方形,用探究的方法可分割为一些1×5或2×3的矩形.
第四部分实际应用的答案如图7所示.图6图7


