数学慢教育的曲线思维及其教学价值
“道可道,非常道;名可名,非常名”这是曲线思维在哲学领域的具象.“两点之间线段最短”的数学基本事实则是直线思维在科学领域的具体表现.而“道不远人”的“大一统”思想则反映了曲线思维的主流文化地位,直线思维的种属学科性质.数学慢教育作为哲学范畴的教学论,概念曲线思维的意识形态特征属于认识信念范畴,表征曲线思维对象的运动形态特征属于方法论范畴[1].进一步而言,曲线思维是以认识信念为思想统领的实践论.就这个层面而言,课题组研究带有鲜明“过程性认识信念”特征的数学慢教育的曲线思维,意义重大,影响深远.
1 数学慢教育中的曲线思维
1.1 数学慢教育曲线思维导图
已有研究表明:动机强度与学习信念之间带有“叶克斯——多德森律”特征,也就是存在“倒U形曲线”关系,动机过强或过弱因信念极端值而效率趋低,只有处于“中值”认知效果最好[2].数学慢教育是以“曲线思维”为突出特征的课程实践论,强调曲线思维在慢教育认知体系中的反复关联作用,关注“无字证明”(数学活动)“二次数学”(变化思想)等直觉行为对曲线思维的指导意义.
美国加利福尼亚州出版的“科学框架”(Science Framework for California Public School)中,将“尺度与结构”“变化与形式”“稳定与演化”“系统与作用”提炼为科学主题[3].
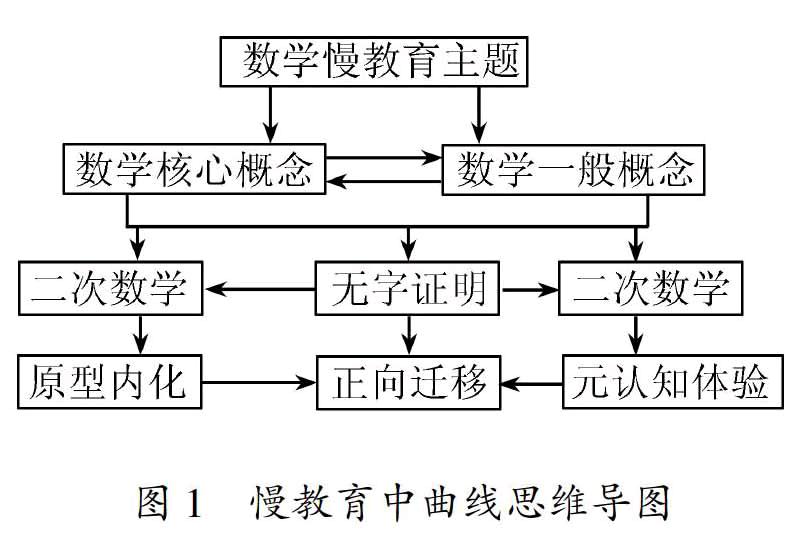
慢教育中的曲线思维层级导图分为四个层次,包括主题的确立(聚焦慢教育主题)、概念的认定(主概念和次概念的划分)、运演的形式(数学活动方式的选择)、心智的内迁(基本思想和基本活动经验的素养倾向)等系统主干因素,终归于曲线思维的定向显化和定性把握.事实上,数学慢教育作为课程实践论揭示曲线思维的“共通性”,即概念的前概念→活动致知概念→反问监控概念→元认知把握概念.这里的“活动”是一个形式化概念,包括二次数学和无字证明等结构思维尺度,而曲线思维就是以“活动事实”为外在形式的思维轨迹.
1.2 什么是曲线思维
曲线思维是物质世界和生命运动的基本形式.没有曲线思维就没有合理的结构和巧妙的造型.“螺旋上升”主宰着曲线思维模式,在这条曲线上走过阿基米德、菲狄亚、达芬奇、达尔文、爱因斯坦等科学大师;在这条曲线上矗立着中国的太极图、古希腊的巴特农神殿、爱奥尼亚的柱头饰、法国布卢瓦的皇家建筑群等艺术奇葩;在这条曲线上排列着植物叶序图、元素周期表、黄金分割线、人体比例图、费氏级数等自然法则.因此,是曲线思维让无序的世界有序化且充满美感.
曲线思维作为教学论,则反映数学慢教育的本体价值.数学慢教育课题研究组认为,曲线思维是一种从直观的知觉思维出发,突出二次数学或多次数学的“过程性”特征,终于概念系的“关系性理解”的思维方式[4].事实上,慢教育数学就是必须让学习者经历“工具性理解→概念性理解→关系性理解”,方能把握数学对象的本质.《义务教育数学课程标准(2011年版)》在课程理念中提出,课程内容的组织要重视过程,处理好过程与结果的关系;要重视直观,处理好直观与抽象的关系等.显然,这就从课程论层面明确指出思维的“过程性”对数学慢教育的反哺意义.田万海先生认为,在数学学习中,学生对数学知识的理解不是一次完成的,其间需要经过初步理解、确切理解和深刻理解三个阶段[5].这就是慢教育研究者提出“多次数学”的思维事实根据.
有人说,好教师教人发现真理,坏教师教人奉送真理.曲线思维研究组认为,让学生看到“思维过程”的教学是“好教学”,剥夺学生“知其所以然”的教学是“差教学”.就形而下的教学“器识”而言,无论是“关系理解”的到达、“深刻理解”的把握、还是“多次数学”的行为以及“所以然”的知性等创造型复合思维的运演,都离不开研究对象的“过程性思维”.而过程的“过程”都带有明显的迂回曲折的特征,在现象学领域呈“波浪前进”的研究趋势.因此,我们把具有创造潜能的复杂多变的概念思维模式定义为曲线思维.
2 曲线思维的教学价值
提高学生的思维素养是数学教育的终极目标.曲线思维作为数学思维领域的一种普遍方法具有普适性和科学性.它揭示慢教育课堂学科思维教育的认识信念,重视问题解决产生式心理原型的形成,反映一个人过程性认识系统的概念能力[6].数学慢教育课堂曲线思维的教学价值表现在以下几个层面.
2.1 有利于学生进行原型内化
在加里培林和安德森(认知阶段、联结阶段和自动化阶段)研究的基础上,我国教育学者提出心智技能形成三段论即原型定向、原型操作和原型内化.“内化”作为心理学俗语,取外部动作向内部转化之意,即内部动作映像形成的过程.比如,学习“探索勾股定理”时,我们选择制作直角三角形教具为“前概念”背景,让学生感受学习这一新知的必要性.进而实现将“现实模型”转化为“心理原型”,终归于概念表象的定向产生.“原型内化”作为心智技能的高级形态,是心智活动的实践模式向头脑内部转化,即由物质的、外显的、展开的形式变成观念的、内潜的、简缩的形式化过程.而数学慢教育课堂的曲线思维是以寻找“前概念”为思维抓手的思维行为,演绎、解释前概念的过程就是心理原型得以内化的过程.

曲线思维是以概念认识系统的定性变迁来实现的.核心概念是曲线思维的研究主题,而一般概念是曲线思维研究的子节点.对于概念的一般性与特殊性的划分则是曲线思维发挥作用的表现,标志认识信念的指向和集中的程度,即曲线思维观念的定量形成.正如上述勾股定理场感描述的那样,情境简单,概念的主次清晰透明,易于理解把握.这就是曲线思维素养层面的慢教育大意.这里我们反对概念行为的直线思维倾向(奉送真理),也反对情境泛滥的“过”曲线思维倾向(作秀式情境).
2.2 有利于学生提高元认知力
提高元认知能力是数学慢教育思维教育的主题.数学元认知能力包括数学元认知知识的掌握与致用能力、数学学习自我规划、自我监控和自我调节能力等[7].元认知作为思维学概念就是对认知的认知,也就是把认知过程作为研究对象.常见的元认知行为就是“反思”“回流”等思维行为.唯有“反思”,方能将知识的学术形态转化为教育形态.多次用“思维”审视概念的行为,能使得问题解决过程逻辑连贯、方法体系共通化、经验体系框架化、思想意识集中化,终归于概念系的来龙去脉.而这些简洁的思维结论,在另一个侧面,反映了曲线思维的反复性和回流性.事实上,元认知本身就是一种带有强烈曲线特征的曲线思维.
慢教育课堂数学元认知包括数学元认知知识、元认知体验与元认知监控,其中元认知体验和监控对学习者的思维锻炼效果明显.在元认知行为实施过程中,我们常以“反问”监控的形式进行曲线思维,伴随着递进式“为什么”的哲学追问.而“做什么”“怎么做”“为什么这样做”“接着,还应做什么”都是曲线思维的典型表现.因此,就监控学的思维过程来说,曲线思维方法能反哺元认知力的能力,提高了课程思维教育力.
2.3 有利于学生学习正向迁移
教育心理学家奥苏泊尔的迁移论,强调认知结构的稳定性、概括性、包容性、连贯性和可辨性等特性始终影响着新知的获得和保持.安德森等人认为,如果两种情境中有产生式的交叉或重叠,则可以产生迁移.加特纳等人认为,若前后两种情境的结构特征相匹配或相同,则迁移产生.这就是当下情境教学论被“第一概念”的意义所在(哲学论范畴).数学慢教育曲线思维带有鲜明的概括性和连贯性思维特征,其思维过程就是建立产生式(是认知的基本成分,由一个或多个条件+动作的配对构成),而运演目标则是实现认知的正向迁移.
诚然,迁移的本质是新旧经验的整合过程.数学慢教育曲线思维的关键词就是整合,这里的“整合”是新旧经验的一体化现象.即借助分析、抽象、综合、概括等数学活动,使新旧经验相互作用,从而形成在结构上一体化、系统化;在功能上可稳定调节活动的一个完整心理系统.慢教育曲线思维的运动线索为:情境(形式化、客观化)→组织(抽象与概括)→观念(思想、方法)→意识(能力、习惯).这与已有研究揭示的学生个体与群体的思维结构有相通之处[8].曲线思维的整合行为可以通过同化、顺应与重组来实现.比如,在探索勾股定理的过程中,让学生任意画一个直角三角形,测量其三边的长度并给出猜想.这一情境能让学生在监控体验中,经历思维内部关系的重组和同化,落实认知正迁移意识观.
3 曲线思维的教学设计框架
已有研究发现数学优生思维具有以下共性特征:(1)善于接近性、相似性和对比性联想;(2)产生块状思维和复合思维;(3)采用弯曲思维(转化);(4)超回归思维[9].可见,运行曲线思维教学概念已成为当下教育界的自然法则,备受学科思维教育的关注和热议.
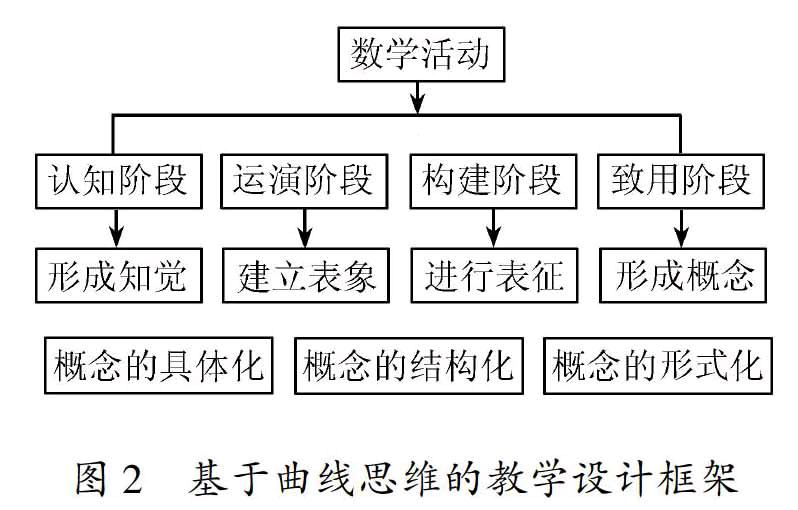
S.Pirie和T.Kieren的超回归数学理解模型,由原始认识、产生表象、形成表象、性质认知、形式化、符号化、构造化、发明创造,这8个过程揭示学习者理解数学概念的全过程[10].数学慢教育研究组提出曲线思维的教学设计框架,主要包括4个反应层级(见图2).
恩格斯说:“数学是研究现实世界的空间形式和数量关系的科学.”我们可以借助概念研究曲线思维的科学框架.概念是数学大厦的“基石”.数学活动的直接目标就是习得概念,间接目标是养护曲线思维,进而影响生命的行事观.由图2可知,数学活动是曲线思维的依附载体,4个阶段(4级思维)是其基本的运动方式,超回归心理模型是其立论的基础,概念的内化和迁移是曲线思维运动的集大成者.在综合思维演变的过程中,形式化曲线思维主要表现在3个层面:一是设计准情境寻找前概念(简明的问题情境),数学科学不允许有前概念,但数学教育学可以有前概念;二是问题组块内部关系逻辑连贯,外在形式开放聚合有序,内在思维黑白相间;三是借助元认知监控行为将核心概念转化为一般概念,这里的一般有“一般”的一般意义,也有形式化的符号意义.
下面以“探索勾股定理”教学为例,对数学慢教育课堂曲线思维运行过程加以说明.
就思维过程学来说,探索勾股定理教学的思维核心是“勾股定理的缘起缘落”,它揭示章节抑或单元起始课的思维线索.为促进学生对章核心概念(勾股定理)的理解,势必需要将曲线思维形式的一般概念转化为具体形式的核心概念,同时还需要将特殊形式的核心概念进行一般化演绎,进而使得概念的理解从内容走向形式,终于概念的关系性理解(见表1).
在这样的科学框架体系内,设计带有明显曲线思维特征的数学活动,使得核心概念突出,一般概念敞亮透明;教学过程主题聚焦,教育过程主题鲜明;过程性思维在哲学追问中螺旋上升,在元认知体验中入乎其内而又出乎其外.就思维科学论而言,4个思维层级的问题都以曲线思维为突出特征,断然屏蔽“两点之间线段最短”的最近意识.正是这种让学生“看得见思维”的曲线思维,才让慢教育课堂不慢而慢,慢而不慢且辩证前行,终归于慢教育形式的简约但思维并不简单的曲线定论.
概言之,慢教育中曲线思维的教学关键是:围绕学生的核心素养设计运演问题“反应块”,在“超回归”心理模型的指导下,进行概念的逻辑划分和回归性监控分析.曲线思维起于核心概念的定性把握,一般概念的定量转化,终于正向行事观的形成.这与教育部课程教育素养指标的培养具有内部系数相关一致性,即社会参与的维度、自主发展的维度和文化修养的维度[11].
参考文献
[1]朱桂凤,孙朝仁.数学慢教育研究综述[J].江苏教育研究,2013(7A):47-50.
[2]王光明,刁颖.高效数学学习的心理特征研究[J].数学教育学报,2009,18(5):51-56.
[3]The California State Board of Education.Science Framework[M].USA:California Department of Education.2000:86-88.
[4]马复.试论数学理解的两种类型——从R.斯根普的工作谈起[J].数学教育学报,2001,10(3):50-51.
[5]田万海.数学教育学[M].杭州:浙江教育出版社,1993∶88-89.
[6]程德胜,喻平.高职学校数学教师认识信念分析与倾向性研究[J].数学教育学报,2015(2):92-97.
[7]王光明.数学教育研究方法与论文写作[M].北京:北京师范大学出版社,2010∶222.
[8]徐文彬.关于数学文化视域中数学学习的构想[J].数学教育学报,2014(5):1.
[9]王光明.数学教育研究方法与论文写作[M].北京:北京师范大学出版社,2010∶228.
[10]李淑文,张同君.“超回归”数学理解模型[J].数学教育学报,2002,11(1):21-23.
[11]王尚志,胡殿顺.齐民友先生对数学教育若干问题的看法——齐民友先生访谈录[J].数学教育学报,2015(2):4-9.
1 数学慢教育中的曲线思维
1.1 数学慢教育曲线思维导图
已有研究表明:动机强度与学习信念之间带有“叶克斯——多德森律”特征,也就是存在“倒U形曲线”关系,动机过强或过弱因信念极端值而效率趋低,只有处于“中值”认知效果最好[2].数学慢教育是以“曲线思维”为突出特征的课程实践论,强调曲线思维在慢教育认知体系中的反复关联作用,关注“无字证明”(数学活动)“二次数学”(变化思想)等直觉行为对曲线思维的指导意义.
美国加利福尼亚州出版的“科学框架”(Science Framework for California Public School)中,将“尺度与结构”“变化与形式”“稳定与演化”“系统与作用”提炼为科学主题[3].

慢教育中的曲线思维层级导图分为四个层次,包括主题的确立(聚焦慢教育主题)、概念的认定(主概念和次概念的划分)、运演的形式(数学活动方式的选择)、心智的内迁(基本思想和基本活动经验的素养倾向)等系统主干因素,终归于曲线思维的定向显化和定性把握.事实上,数学慢教育作为课程实践论揭示曲线思维的“共通性”,即概念的前概念→活动致知概念→反问监控概念→元认知把握概念.这里的“活动”是一个形式化概念,包括二次数学和无字证明等结构思维尺度,而曲线思维就是以“活动事实”为外在形式的思维轨迹.
1.2 什么是曲线思维
曲线思维是物质世界和生命运动的基本形式.没有曲线思维就没有合理的结构和巧妙的造型.“螺旋上升”主宰着曲线思维模式,在这条曲线上走过阿基米德、菲狄亚、达芬奇、达尔文、爱因斯坦等科学大师;在这条曲线上矗立着中国的太极图、古希腊的巴特农神殿、爱奥尼亚的柱头饰、法国布卢瓦的皇家建筑群等艺术奇葩;在这条曲线上排列着植物叶序图、元素周期表、黄金分割线、人体比例图、费氏级数等自然法则.因此,是曲线思维让无序的世界有序化且充满美感.
曲线思维作为教学论,则反映数学慢教育的本体价值.数学慢教育课题研究组认为,曲线思维是一种从直观的知觉思维出发,突出二次数学或多次数学的“过程性”特征,终于概念系的“关系性理解”的思维方式[4].事实上,慢教育数学就是必须让学习者经历“工具性理解→概念性理解→关系性理解”,方能把握数学对象的本质.《义务教育数学课程标准(2011年版)》在课程理念中提出,课程内容的组织要重视过程,处理好过程与结果的关系;要重视直观,处理好直观与抽象的关系等.显然,这就从课程论层面明确指出思维的“过程性”对数学慢教育的反哺意义.田万海先生认为,在数学学习中,学生对数学知识的理解不是一次完成的,其间需要经过初步理解、确切理解和深刻理解三个阶段[5].这就是慢教育研究者提出“多次数学”的思维事实根据.

有人说,好教师教人发现真理,坏教师教人奉送真理.曲线思维研究组认为,让学生看到“思维过程”的教学是“好教学”,剥夺学生“知其所以然”的教学是“差教学”.就形而下的教学“器识”而言,无论是“关系理解”的到达、“深刻理解”的把握、还是“多次数学”的行为以及“所以然”的知性等创造型复合思维的运演,都离不开研究对象的“过程性思维”.而过程的“过程”都带有明显的迂回曲折的特征,在现象学领域呈“波浪前进”的研究趋势.因此,我们把具有创造潜能的复杂多变的概念思维模式定义为曲线思维.
2 曲线思维的教学价值
提高学生的思维素养是数学教育的终极目标.曲线思维作为数学思维领域的一种普遍方法具有普适性和科学性.它揭示慢教育课堂学科思维教育的认识信念,重视问题解决产生式心理原型的形成,反映一个人过程性认识系统的概念能力[6].数学慢教育课堂曲线思维的教学价值表现在以下几个层面.
2.1 有利于学生进行原型内化
在加里培林和安德森(认知阶段、联结阶段和自动化阶段)研究的基础上,我国教育学者提出心智技能形成三段论即原型定向、原型操作和原型内化.“内化”作为心理学俗语,取外部动作向内部转化之意,即内部动作映像形成的过程.比如,学习“探索勾股定理”时,我们选择制作直角三角形教具为“前概念”背景,让学生感受学习这一新知的必要性.进而实现将“现实模型”转化为“心理原型”,终归于概念表象的定向产生.“原型内化”作为心智技能的高级形态,是心智活动的实践模式向头脑内部转化,即由物质的、外显的、展开的形式变成观念的、内潜的、简缩的形式化过程.而数学慢教育课堂的曲线思维是以寻找“前概念”为思维抓手的思维行为,演绎、解释前概念的过程就是心理原型得以内化的过程.

曲线思维是以概念认识系统的定性变迁来实现的.核心概念是曲线思维的研究主题,而一般概念是曲线思维研究的子节点.对于概念的一般性与特殊性的划分则是曲线思维发挥作用的表现,标志认识信念的指向和集中的程度,即曲线思维观念的定量形成.正如上述勾股定理场感描述的那样,情境简单,概念的主次清晰透明,易于理解把握.这就是曲线思维素养层面的慢教育大意.这里我们反对概念行为的直线思维倾向(奉送真理),也反对情境泛滥的“过”曲线思维倾向(作秀式情境).
2.2 有利于学生提高元认知力
提高元认知能力是数学慢教育思维教育的主题.数学元认知能力包括数学元认知知识的掌握与致用能力、数学学习自我规划、自我监控和自我调节能力等[7].元认知作为思维学概念就是对认知的认知,也就是把认知过程作为研究对象.常见的元认知行为就是“反思”“回流”等思维行为.唯有“反思”,方能将知识的学术形态转化为教育形态.多次用“思维”审视概念的行为,能使得问题解决过程逻辑连贯、方法体系共通化、经验体系框架化、思想意识集中化,终归于概念系的来龙去脉.而这些简洁的思维结论,在另一个侧面,反映了曲线思维的反复性和回流性.事实上,元认知本身就是一种带有强烈曲线特征的曲线思维.
慢教育课堂数学元认知包括数学元认知知识、元认知体验与元认知监控,其中元认知体验和监控对学习者的思维锻炼效果明显.在元认知行为实施过程中,我们常以“反问”监控的形式进行曲线思维,伴随着递进式“为什么”的哲学追问.而“做什么”“怎么做”“为什么这样做”“接着,还应做什么”都是曲线思维的典型表现.因此,就监控学的思维过程来说,曲线思维方法能反哺元认知力的能力,提高了课程思维教育力.
2.3 有利于学生学习正向迁移
教育心理学家奥苏泊尔的迁移论,强调认知结构的稳定性、概括性、包容性、连贯性和可辨性等特性始终影响着新知的获得和保持.安德森等人认为,如果两种情境中有产生式的交叉或重叠,则可以产生迁移.加特纳等人认为,若前后两种情境的结构特征相匹配或相同,则迁移产生.这就是当下情境教学论被“第一概念”的意义所在(哲学论范畴).数学慢教育曲线思维带有鲜明的概括性和连贯性思维特征,其思维过程就是建立产生式(是认知的基本成分,由一个或多个条件+动作的配对构成),而运演目标则是实现认知的正向迁移.
诚然,迁移的本质是新旧经验的整合过程.数学慢教育曲线思维的关键词就是整合,这里的“整合”是新旧经验的一体化现象.即借助分析、抽象、综合、概括等数学活动,使新旧经验相互作用,从而形成在结构上一体化、系统化;在功能上可稳定调节活动的一个完整心理系统.慢教育曲线思维的运动线索为:情境(形式化、客观化)→组织(抽象与概括)→观念(思想、方法)→意识(能力、习惯).这与已有研究揭示的学生个体与群体的思维结构有相通之处[8].曲线思维的整合行为可以通过同化、顺应与重组来实现.比如,在探索勾股定理的过程中,让学生任意画一个直角三角形,测量其三边的长度并给出猜想.这一情境能让学生在监控体验中,经历思维内部关系的重组和同化,落实认知正迁移意识观.
3 曲线思维的教学设计框架
已有研究发现数学优生思维具有以下共性特征:(1)善于接近性、相似性和对比性联想;(2)产生块状思维和复合思维;(3)采用弯曲思维(转化);(4)超回归思维[9].可见,运行曲线思维教学概念已成为当下教育界的自然法则,备受学科思维教育的关注和热议.
S.Pirie和T.Kieren的超回归数学理解模型,由原始认识、产生表象、形成表象、性质认知、形式化、符号化、构造化、发明创造,这8个过程揭示学习者理解数学概念的全过程[10].数学慢教育研究组提出曲线思维的教学设计框架,主要包括4个反应层级(见图2).
恩格斯说:“数学是研究现实世界的空间形式和数量关系的科学.”我们可以借助概念研究曲线思维的科学框架.概念是数学大厦的“基石”.数学活动的直接目标就是习得概念,间接目标是养护曲线思维,进而影响生命的行事观.由图2可知,数学活动是曲线思维的依附载体,4个阶段(4级思维)是其基本的运动方式,超回归心理模型是其立论的基础,概念的内化和迁移是曲线思维运动的集大成者.在综合思维演变的过程中,形式化曲线思维主要表现在3个层面:一是设计准情境寻找前概念(简明的问题情境),数学科学不允许有前概念,但数学教育学可以有前概念;二是问题组块内部关系逻辑连贯,外在形式开放聚合有序,内在思维黑白相间;三是借助元认知监控行为将核心概念转化为一般概念,这里的一般有“一般”的一般意义,也有形式化的符号意义.
下面以“探索勾股定理”教学为例,对数学慢教育课堂曲线思维运行过程加以说明.
就思维过程学来说,探索勾股定理教学的思维核心是“勾股定理的缘起缘落”,它揭示章节抑或单元起始课的思维线索.为促进学生对章核心概念(勾股定理)的理解,势必需要将曲线思维形式的一般概念转化为具体形式的核心概念,同时还需要将特殊形式的核心概念进行一般化演绎,进而使得概念的理解从内容走向形式,终于概念的关系性理解(见表1).
在这样的科学框架体系内,设计带有明显曲线思维特征的数学活动,使得核心概念突出,一般概念敞亮透明;教学过程主题聚焦,教育过程主题鲜明;过程性思维在哲学追问中螺旋上升,在元认知体验中入乎其内而又出乎其外.就思维科学论而言,4个思维层级的问题都以曲线思维为突出特征,断然屏蔽“两点之间线段最短”的最近意识.正是这种让学生“看得见思维”的曲线思维,才让慢教育课堂不慢而慢,慢而不慢且辩证前行,终归于慢教育形式的简约但思维并不简单的曲线定论.
概言之,慢教育中曲线思维的教学关键是:围绕学生的核心素养设计运演问题“反应块”,在“超回归”心理模型的指导下,进行概念的逻辑划分和回归性监控分析.曲线思维起于核心概念的定性把握,一般概念的定量转化,终于正向行事观的形成.这与教育部课程教育素养指标的培养具有内部系数相关一致性,即社会参与的维度、自主发展的维度和文化修养的维度[11].
参考文献
[1]朱桂凤,孙朝仁.数学慢教育研究综述[J].江苏教育研究,2013(7A):47-50.
[2]王光明,刁颖.高效数学学习的心理特征研究[J].数学教育学报,2009,18(5):51-56.
[3]The California State Board of Education.Science Framework[M].USA:California Department of Education.2000:86-88.
[4]马复.试论数学理解的两种类型——从R.斯根普的工作谈起[J].数学教育学报,2001,10(3):50-51.
[5]田万海.数学教育学[M].杭州:浙江教育出版社,1993∶88-89.
[6]程德胜,喻平.高职学校数学教师认识信念分析与倾向性研究[J].数学教育学报,2015(2):92-97.
[7]王光明.数学教育研究方法与论文写作[M].北京:北京师范大学出版社,2010∶222.
[8]徐文彬.关于数学文化视域中数学学习的构想[J].数学教育学报,2014(5):1.
[9]王光明.数学教育研究方法与论文写作[M].北京:北京师范大学出版社,2010∶228.
[10]李淑文,张同君.“超回归”数学理解模型[J].数学教育学报,2002,11(1):21-23.
[11]王尚志,胡殿顺.齐民友先生对数学教育若干问题的看法——齐民友先生访谈录[J].数学教育学报,2015(2):4-9.

