方程求解的算法情景化
孙学东
算法是对一类问题的机械的、统一的求解方法.解方程是一个由已知推求未知的运算过程,它有较一致的方法和步骤,是算法思想的重要应用.因为方程求解的程序性,学生即便对算理不理解,套套程序,也能够获得方程的解,所以日常教学中,方程求解的原理多不受重视.重解方程的“操作性”,轻解方程原理的“理解性”,其后果往往是学生不会选择合适简洁的解法,缺少对解法合理性的批判能力,从而也就难以形成用方程解决实际问题的能力.
算法化是我国古代数学的重要特色[1],以《九章算术》为例,其内容丰富而且实用性强,以解决生产生活的问题为中心,在解题中给出算法,再根据算法组建理论体系.显然,我国古算法即强调融算理于实际情景,在实际情景的应用中演绎算法步骤.初中阶段涉及的方程主要是一元一次方程、二元一次方程、分式方程和一元二次方程,本文拟构造几个实际情景,并分析上述方程在实际情景中的求解过程,以观察方程求解算法情景化的教学意义.
1 数学符号的内涵操作凸显方程算法的思维过程
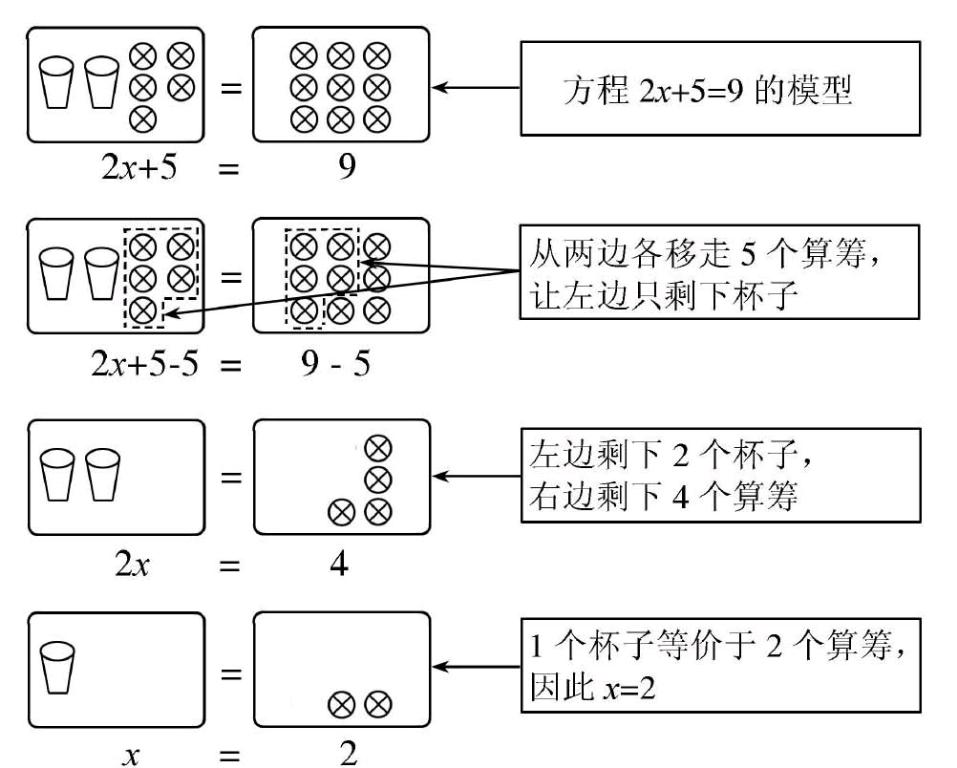
在学习解一元一次方程时,我们常常会出示下面的情景[2]:
显然,这是用学具操作来帮助学生理解方程求解的过程,但是学具只是数字和符号的替代品,操作过程只是对符号操作的检验.为让学生既能感受算法的合理性,也能自觉总结算法步骤,可设置下面的问题情景:
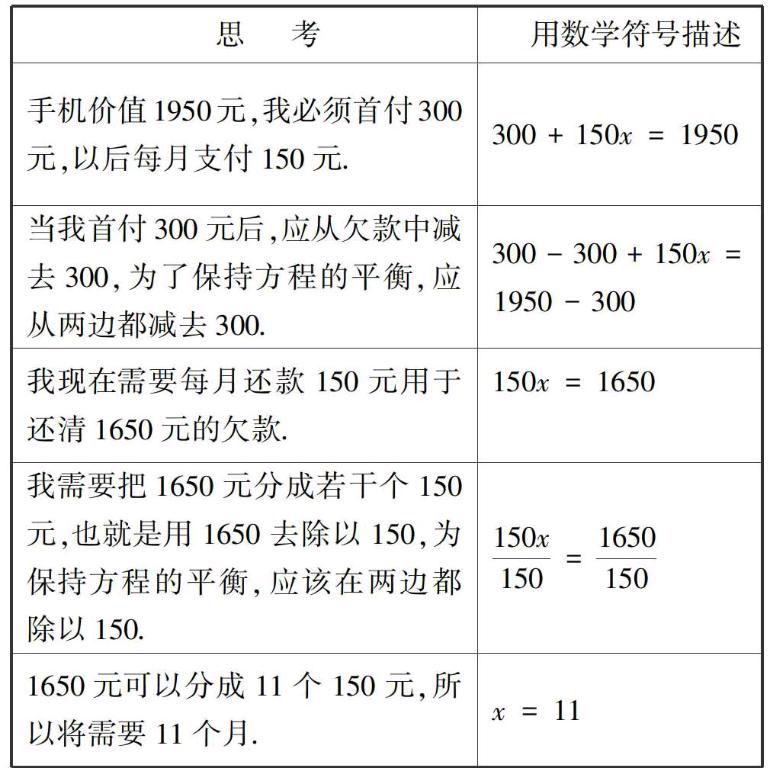
情景1 某手机卖场为了促销一款价值1950元的手机,允许顾客按月分期付款.顾客首付300元,以后每月支付150元.如果你以按月分期付款的方式购买这款手机,需要多少个月才能付清全部款项?解释你的解题过程.为了更好的理解题意,你可以先写出解题的思考步骤,再试着用数学符号去描述这些步骤.
分析 实际教学中,我们会感觉上述一元一次方程的求解过程是简单的,只需要让学生理解并熟练使用“移项(要变号)、合并同类项、化系数为1”这一程序就行了,设置情景反倒会降低学生的学习注意力,影响课堂的效率.事实上,算法情景化的本意就是让学生感受程序性的解题过程与生活实际是一致的.这样处理既能让学生理解算法程序的合理性,也能提升数学问题的思维含量,从而让学生感受数学学习的内蕴,也为以后分析较困难的实际问题做好了铺垫.

情景1较前一个情景,虽然不够直观,但对于小学时已经接触过简单方程的初中生来说,情景1的价值在于它似乎更能在实际问题解决的过程中,让学生感受方程求解过程的合理性,从而自觉的总结一元一次方程的算法步骤.
2 古算法与方程思想的对比彰显方程求解过程的现实意义
情景2 七年级某班共有学生32人,参加拔河比赛获得优胜,并得到每箱24瓶的运动饮料6箱作为奖励.老师打算发给参加比赛的学生每人6瓶,在旁加油的学生每人若干瓶(少于6瓶),并且能恰好将运动饮料分完.则在旁加油的学生每人可能分到多少瓶?
分析 问题情景中“并且能恰好将运动饮料分完”取决于两个因素,一个是参加拔河的人数(或者在旁加油的人数),另一个是在旁加油的学生每人分得的瓶数.因此,本题是一个有两个变量,但是只有一个等量关系的不定方程问题.二元一次不定方程的解有无数组,但是正整数解只有有限组,因此求得“在旁加油的学生每人可能分到多少瓶”是有可能的.设在旁加油的学生每人分得x瓶,有y个运动员,根据题意可得方程:(32-y)·x+6y=24×6,
随着分式方程的不断化简,相应的分式方程也越来越体现问题情景的本质内涵.方程求解的算法过程与实际情景的现实意义相辅相成,学生对于问题情景本质的理解所产生的思维震撼也越来越外显,越来越逼真.
4 情景规律的背后是方程求解算法原理的丰富

情景4 某地发生了流感疫情,假如在人群中一人患了流感,经过两轮传染后共有121人患流感.问在每轮传染中平均每人传染几人?
分析 传染流感的过程中若设每轮传染中平均一个人传染x个人,那么患流感的这个人第一轮传染后共有(x+1)人患了流感;在第二轮传染中传染源是(x+1)人,这些人中每个人又传染了x人,那么第二轮新传染了x(x+1)人,于是第二轮传染后共有(x+1)+x(x+1)人患流感.而(x+1)+x(x+1)因式分解后是(x+1)2,于是这个情景所对应的方程就是(x+1)2=121.
追问:第三轮传染后患流感的人数会是(x+1)3吗?在第三轮传染中传染源是(x+1)2人,这些人中每个人又传染了x人,那么第三轮新传染了x(x+1)2人,于是第三轮传染后共有(x+1)2+x(x+1)2人患流感.而(x+1)2+x(x+1)2因式分解后恰是(x+1)3.到此,我们可以大胆地猜测,第n轮后,将有(x+1)n人患了流感.
如果说情景3所体现的是方程求解在化归过程(逐步变形化简)中产生的对情景的深入理解,那么情景4则是情景规律的分析过程中对方程求解的算法原理的不断丰富.
由以上的情景及分析,我们能发现,方程求解的算法情景化体现了数学知识内部的联系与一致性,是数学“求真”、“求美”内蕴的外显.“情景化”不是“去数学化”,相反的是让学生在情景中更理性地分析算法的合理性,同时方程求解中的算法原理及变形过程往往也富含着情景中的现实意义,促使我们对问题情景的不同角度的深入的认识.
参考文献
[1]王渝生.中国算学史[M].上海:上海人民出版社,200610:18.
[2]聂必凯等.美国现代数学教育改革[M].人民教育出版社,20106:118.
算法是对一类问题的机械的、统一的求解方法.解方程是一个由已知推求未知的运算过程,它有较一致的方法和步骤,是算法思想的重要应用.因为方程求解的程序性,学生即便对算理不理解,套套程序,也能够获得方程的解,所以日常教学中,方程求解的原理多不受重视.重解方程的“操作性”,轻解方程原理的“理解性”,其后果往往是学生不会选择合适简洁的解法,缺少对解法合理性的批判能力,从而也就难以形成用方程解决实际问题的能力.
算法化是我国古代数学的重要特色[1],以《九章算术》为例,其内容丰富而且实用性强,以解决生产生活的问题为中心,在解题中给出算法,再根据算法组建理论体系.显然,我国古算法即强调融算理于实际情景,在实际情景的应用中演绎算法步骤.初中阶段涉及的方程主要是一元一次方程、二元一次方程、分式方程和一元二次方程,本文拟构造几个实际情景,并分析上述方程在实际情景中的求解过程,以观察方程求解算法情景化的教学意义.
1 数学符号的内涵操作凸显方程算法的思维过程

在学习解一元一次方程时,我们常常会出示下面的情景[2]:

显然,这是用学具操作来帮助学生理解方程求解的过程,但是学具只是数字和符号的替代品,操作过程只是对符号操作的检验.为让学生既能感受算法的合理性,也能自觉总结算法步骤,可设置下面的问题情景:
情景1 某手机卖场为了促销一款价值1950元的手机,允许顾客按月分期付款.顾客首付300元,以后每月支付150元.如果你以按月分期付款的方式购买这款手机,需要多少个月才能付清全部款项?解释你的解题过程.为了更好的理解题意,你可以先写出解题的思考步骤,再试着用数学符号去描述这些步骤.
分析 实际教学中,我们会感觉上述一元一次方程的求解过程是简单的,只需要让学生理解并熟练使用“移项(要变号)、合并同类项、化系数为1”这一程序就行了,设置情景反倒会降低学生的学习注意力,影响课堂的效率.事实上,算法情景化的本意就是让学生感受程序性的解题过程与生活实际是一致的.这样处理既能让学生理解算法程序的合理性,也能提升数学问题的思维含量,从而让学生感受数学学习的内蕴,也为以后分析较困难的实际问题做好了铺垫.

情景1较前一个情景,虽然不够直观,但对于小学时已经接触过简单方程的初中生来说,情景1的价值在于它似乎更能在实际问题解决的过程中,让学生感受方程求解过程的合理性,从而自觉的总结一元一次方程的算法步骤.
2 古算法与方程思想的对比彰显方程求解过程的现实意义
情景2 七年级某班共有学生32人,参加拔河比赛获得优胜,并得到每箱24瓶的运动饮料6箱作为奖励.老师打算发给参加比赛的学生每人6瓶,在旁加油的学生每人若干瓶(少于6瓶),并且能恰好将运动饮料分完.则在旁加油的学生每人可能分到多少瓶?
分析 问题情景中“并且能恰好将运动饮料分完”取决于两个因素,一个是参加拔河的人数(或者在旁加油的人数),另一个是在旁加油的学生每人分得的瓶数.因此,本题是一个有两个变量,但是只有一个等量关系的不定方程问题.二元一次不定方程的解有无数组,但是正整数解只有有限组,因此求得“在旁加油的学生每人可能分到多少瓶”是有可能的.设在旁加油的学生每人分得x瓶,有y个运动员,根据题意可得方程:(32-y)·x+6y=24×6,
随着分式方程的不断化简,相应的分式方程也越来越体现问题情景的本质内涵.方程求解的算法过程与实际情景的现实意义相辅相成,学生对于问题情景本质的理解所产生的思维震撼也越来越外显,越来越逼真.
4 情景规律的背后是方程求解算法原理的丰富

情景4 某地发生了流感疫情,假如在人群中一人患了流感,经过两轮传染后共有121人患流感.问在每轮传染中平均每人传染几人?
分析 传染流感的过程中若设每轮传染中平均一个人传染x个人,那么患流感的这个人第一轮传染后共有(x+1)人患了流感;在第二轮传染中传染源是(x+1)人,这些人中每个人又传染了x人,那么第二轮新传染了x(x+1)人,于是第二轮传染后共有(x+1)+x(x+1)人患流感.而(x+1)+x(x+1)因式分解后是(x+1)2,于是这个情景所对应的方程就是(x+1)2=121.
追问:第三轮传染后患流感的人数会是(x+1)3吗?在第三轮传染中传染源是(x+1)2人,这些人中每个人又传染了x人,那么第三轮新传染了x(x+1)2人,于是第三轮传染后共有(x+1)2+x(x+1)2人患流感.而(x+1)2+x(x+1)2因式分解后恰是(x+1)3.到此,我们可以大胆地猜测,第n轮后,将有(x+1)n人患了流感.
如果说情景3所体现的是方程求解在化归过程(逐步变形化简)中产生的对情景的深入理解,那么情景4则是情景规律的分析过程中对方程求解的算法原理的不断丰富.
由以上的情景及分析,我们能发现,方程求解的算法情景化体现了数学知识内部的联系与一致性,是数学“求真”、“求美”内蕴的外显.“情景化”不是“去数学化”,相反的是让学生在情景中更理性地分析算法的合理性,同时方程求解中的算法原理及变形过程往往也富含着情景中的现实意义,促使我们对问题情景的不同角度的深入的认识.
参考文献
[1]王渝生.中国算学史[M].上海:上海人民出版社,200610:18.
[2]聂必凯等.美国现代数学教育改革[M].人民教育出版社,20106:118.

