引导学生发现、感悟证明几何定理的一个新作法
秦旭东

1问题的提出
2011年版义务教育课标要求:对几何定理的教学,要以探索与证明的流程来进行.对一些基本定理如三角形内角和定理、平行四边形的性质定理、三角形中位线定理、三角形相似的预备定理等,如何有效引导学生发现、悟出证明的基本思路,来提高课堂效率呢?经过探索、总结近几年课改成功经验和优秀课例得出:基本定理的教学应按照“生成、发现、分离、复原与论证”这样一条基本思路来进行.实践也证明:基本定理的证明方法和证明时运用的数学思想方法,对其相关定理的教学起到奠基作用.现以课例的形式,将基本定理用这一基本思路来操作介绍如下:
2基本操作方法介绍
三角形的内角和
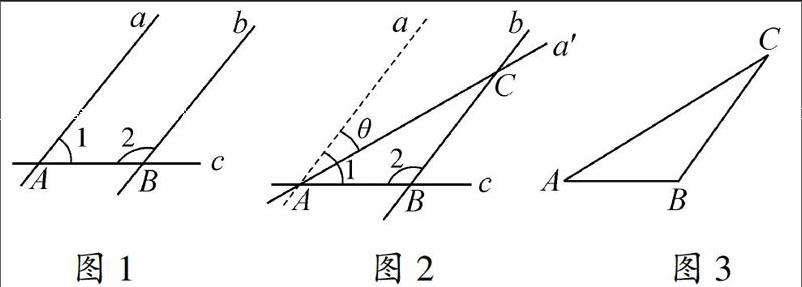
(一)(生成)如图1,直线a、b与直线c分别相交于A、B两点,且a∥b.问学生:
1.此时,∠1与∠2的和是多少?(180°)为什么?(两直线平行,同旁内角互补).
2.若将直线a绕A点顺时针旋转一定的角度θ(不妨让0<θ<∠1),且不与c直线重合,记为a′,问a′与b相交吗?(相交).
3.设直线a′与b相交于C点,如图2所示,那么点A、点B、点C所构成的几何图形是什么图形?(三角形).
4.在图(2)中,∠θ与哪个角相等?为什么?(∠θ=∠ACB,两直线平行,内错角相等).
5.(发现)问图2中∠CAB+∠ABC+∠ACB与∠1+∠2有何大小关系呢?是多少?(相等,180°).
(二)(分离)若从图2中分离出△ABC来,即图3,那么∠A+∠B+∠C的和变吗?(不变).
1.请同学们想一想,如何运用已学知识来证明如图3所示的△ABC的内角和是180°呢?
预设引导:(根据学生情况可能用到的提示.下同)
①问初中已学几何知识中,与180°有关的知识有哪些?(平角;邻补角;两直线平行,同旁内角互补).
②如何将三角形的三个内角转化成一个平角或邻补角或两直线平行后的同旁内角呢?请同学们联系前面发现结论的过程想一想,该如何做?
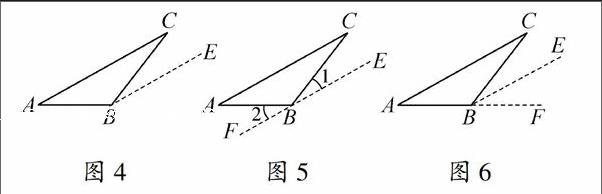
2.(复原与论证)过任意一个顶点作另一边的平行线:如
方法①如图4所示,过B点作BE∥AC的射线BE;
方法②如图5所示,过B点作BE∥AC的直线EF,注意∠1,∠2分别与哪个角相等?
方法③如图6所示,过B点作BE∥AC的射线,并延长AB至F等.
3.反问学生,对任意一个三角形,采用上述方法能够证明它的内角和是180°吗?(能)
从而说明上述方法具有一般性:即三角形的内角和等于180°.证明的基本方法是将其转化为邻补角或平角或互补角来实现.
平行四边形的性质定理
(一)(生成)如图7,在△ABC中,不妨过C点作CD∥BA,过A作AD∥BC,CD与AD交于点D.问学生:
1.图中四边形ABCD在小学称之为什么四边形?(平行四边形).
2.(发现)运用你已掌握的知识,说一说图形中有无相等的线段,相等的角呢?(AB=CD,AD=BC,∠B=∠D,∠BAD=∠DCB)并给出得到结论的理由.(利用△ABC≌△CDA).
(二)(分离)若将图7中的线段AC擦去,就得到图8.问:
1.上面得到的线段相等、角相等还相等吗?(相等)
2.在图8中,已知CD∥BA,AD∥BC,怎样去证明AB=CD,AD=BC,∠B=∠D,∠A=∠C呢?
预设引导:
①说明与证明线段相等的已学知识有哪些?(线段中点知识;等腰三角形知识;全等三角形知识),结合图8、已知内容,根据你的理解,哪些知识与本证明问题联系不上?(线段中点知识;等腰三角形知识).
②如何将平行四边形转化成两个全等三角形呢?
3.(复原与论证)连接任意一条对角线.
方法①:如图9所示,连接AC,通过证明△ABC≌△CDA来得出结论.
方法②:连接BD,通过证明△ABD≌△CDB来得出结论.
4.任意画一个平行四边形ABCD,那么它的对边相等、对角相等吗?(相等)如何证明呢?(方法同上).
平行四边形的对边相等,对角相等,证明的基本方法是将其转化在两个全等三角形中来实现.
三角形的中位线
(一)(生成)如图10所示,ABCD中,E,F分别是AB,CD的中点,连接EF,AC(BD),H是EF与AC的交点.问学生:
1.EF与BC(AD)有怎样的位置关系?(平行)有怎样的数量关系?(相等)为什么呢?(用平行四边形的判定方法与性质来说明).
2.H点具有什么样的特殊性?(H点为AC的中点)怎样去证明呢?(利用△AHE≌△CHF来说明).
3.(发现)在△ABC中,E,H点分别是AB,AC的中点,那么EH与BC有怎样的位置和数量关系呢?(EH∥BC,EH=12BC).
(二)(分离)若将图10中的△ABC分离出来即图11,那么EH∥BC,EH=12BC还成立吗?(成立).
1.请同学们想一想,在图11中,当E、H分别为AB、AC中点时,有EH∥BC,EH=12BC吗?
预设引导:
①你学过哪些知识可供用来判断两线平行呢?(平行线的判断方法;借助某个四边形,先判定它是平行四边形,再得两线平行).
②在图11中,有角等或互补的条件吗?(无).
因此证明EH要平行BC,就只剩下构造并证明某个四边形是平行四边形后,再来得出结论了.
③在图11中,如何构造出的平行四边形,才能有EH的2倍等于BC或BC的一半等于EH呢?
2.(复原与证明)
方法①:延长EH(或HE,略.下同)至F,使EH=HF,连接CF,如图12所示,通过证明△AHE≌△CHF,得到∠A=∠HCF,AE=CF,从而说明四边形BCFE是平行四边形,则EH∥BC,EH=12BC.
方法②:过C(或B)点作CF∥AB,延长EH与CF交于点F,先说明△CFH≌△AEH,进而得到HF=EH,CF=AE=BE来说明四边形BCFE是平行四边形,则EH∥BC,EH=12BC.
方法③:过A点作AD∥BC,过H(或E)点作HD∥AB,HD与AD交于点D,与BC交于点F,如图13所示,易得∠FCH=∠DAH,四边形ABFD是平行四边形,AD=BF,进而说明△ADH≌△CFH,则AD=CF,DH=HF,所以四边形AEHD是平行四边形,则EH∥BC,EH=12BC.
3.对任意一个三角形,若已知两边的中点,那么这两中点的连线,具有上述性质吗?(有)说理方法相同吗?(相同)
三角形的中位线平行于第三边,且等于第三边的一半.说明的基本方法就是通过构造平行四边形来完成的(已学知识是在不包含基本事实:两直线被一组平行线所截,所得的对应线段成比例的前提下).



1问题的提出
2011年版义务教育课标要求:对几何定理的教学,要以探索与证明的流程来进行.对一些基本定理如三角形内角和定理、平行四边形的性质定理、三角形中位线定理、三角形相似的预备定理等,如何有效引导学生发现、悟出证明的基本思路,来提高课堂效率呢?经过探索、总结近几年课改成功经验和优秀课例得出:基本定理的教学应按照“生成、发现、分离、复原与论证”这样一条基本思路来进行.实践也证明:基本定理的证明方法和证明时运用的数学思想方法,对其相关定理的教学起到奠基作用.现以课例的形式,将基本定理用这一基本思路来操作介绍如下:
2基本操作方法介绍
三角形的内角和
(一)(生成)如图1,直线a、b与直线c分别相交于A、B两点,且a∥b.问学生:
1.此时,∠1与∠2的和是多少?(180°)为什么?(两直线平行,同旁内角互补).
2.若将直线a绕A点顺时针旋转一定的角度θ(不妨让0<θ<∠1),且不与c直线重合,记为a′,问a′与b相交吗?(相交).
3.设直线a′与b相交于C点,如图2所示,那么点A、点B、点C所构成的几何图形是什么图形?(三角形).
4.在图(2)中,∠θ与哪个角相等?为什么?(∠θ=∠ACB,两直线平行,内错角相等).
5.(发现)问图2中∠CAB+∠ABC+∠ACB与∠1+∠2有何大小关系呢?是多少?(相等,180°).
(二)(分离)若从图2中分离出△ABC来,即图3,那么∠A+∠B+∠C的和变吗?(不变).
1.请同学们想一想,如何运用已学知识来证明如图3所示的△ABC的内角和是180°呢?
预设引导:(根据学生情况可能用到的提示.下同)
①问初中已学几何知识中,与180°有关的知识有哪些?(平角;邻补角;两直线平行,同旁内角互补).
②如何将三角形的三个内角转化成一个平角或邻补角或两直线平行后的同旁内角呢?请同学们联系前面发现结论的过程想一想,该如何做?
2.(复原与论证)过任意一个顶点作另一边的平行线:如
方法①如图4所示,过B点作BE∥AC的射线BE;
方法②如图5所示,过B点作BE∥AC的直线EF,注意∠1,∠2分别与哪个角相等?
方法③如图6所示,过B点作BE∥AC的射线,并延长AB至F等.
3.反问学生,对任意一个三角形,采用上述方法能够证明它的内角和是180°吗?(能)
从而说明上述方法具有一般性:即三角形的内角和等于180°.证明的基本方法是将其转化为邻补角或平角或互补角来实现.
平行四边形的性质定理
(一)(生成)如图7,在△ABC中,不妨过C点作CD∥BA,过A作AD∥BC,CD与AD交于点D.问学生:
1.图中四边形ABCD在小学称之为什么四边形?(平行四边形).
2.(发现)运用你已掌握的知识,说一说图形中有无相等的线段,相等的角呢?(AB=CD,AD=BC,∠B=∠D,∠BAD=∠DCB)并给出得到结论的理由.(利用△ABC≌△CDA).
(二)(分离)若将图7中的线段AC擦去,就得到图8.问:
1.上面得到的线段相等、角相等还相等吗?(相等)
2.在图8中,已知CD∥BA,AD∥BC,怎样去证明AB=CD,AD=BC,∠B=∠D,∠A=∠C呢?
预设引导:
①说明与证明线段相等的已学知识有哪些?(线段中点知识;等腰三角形知识;全等三角形知识),结合图8、已知内容,根据你的理解,哪些知识与本证明问题联系不上?(线段中点知识;等腰三角形知识).
②如何将平行四边形转化成两个全等三角形呢?
3.(复原与论证)连接任意一条对角线.
方法①:如图9所示,连接AC,通过证明△ABC≌△CDA来得出结论.
方法②:连接BD,通过证明△ABD≌△CDB来得出结论.
4.任意画一个平行四边形ABCD,那么它的对边相等、对角相等吗?(相等)如何证明呢?(方法同上).
平行四边形的对边相等,对角相等,证明的基本方法是将其转化在两个全等三角形中来实现.
三角形的中位线
(一)(生成)如图10所示,ABCD中,E,F分别是AB,CD的中点,连接EF,AC(BD),H是EF与AC的交点.问学生:
1.EF与BC(AD)有怎样的位置关系?(平行)有怎样的数量关系?(相等)为什么呢?(用平行四边形的判定方法与性质来说明).
2.H点具有什么样的特殊性?(H点为AC的中点)怎样去证明呢?(利用△AHE≌△CHF来说明).
3.(发现)在△ABC中,E,H点分别是AB,AC的中点,那么EH与BC有怎样的位置和数量关系呢?(EH∥BC,EH=12BC).
(二)(分离)若将图10中的△ABC分离出来即图11,那么EH∥BC,EH=12BC还成立吗?(成立).
1.请同学们想一想,在图11中,当E、H分别为AB、AC中点时,有EH∥BC,EH=12BC吗?
预设引导:
①你学过哪些知识可供用来判断两线平行呢?(平行线的判断方法;借助某个四边形,先判定它是平行四边形,再得两线平行).
②在图11中,有角等或互补的条件吗?(无).
因此证明EH要平行BC,就只剩下构造并证明某个四边形是平行四边形后,再来得出结论了.
③在图11中,如何构造出的平行四边形,才能有EH的2倍等于BC或BC的一半等于EH呢?
2.(复原与证明)
方法①:延长EH(或HE,略.下同)至F,使EH=HF,连接CF,如图12所示,通过证明△AHE≌△CHF,得到∠A=∠HCF,AE=CF,从而说明四边形BCFE是平行四边形,则EH∥BC,EH=12BC.
方法②:过C(或B)点作CF∥AB,延长EH与CF交于点F,先说明△CFH≌△AEH,进而得到HF=EH,CF=AE=BE来说明四边形BCFE是平行四边形,则EH∥BC,EH=12BC.
方法③:过A点作AD∥BC,过H(或E)点作HD∥AB,HD与AD交于点D,与BC交于点F,如图13所示,易得∠FCH=∠DAH,四边形ABFD是平行四边形,AD=BF,进而说明△ADH≌△CFH,则AD=CF,DH=HF,所以四边形AEHD是平行四边形,则EH∥BC,EH=12BC.
3.对任意一个三角形,若已知两边的中点,那么这两中点的连线,具有上述性质吗?(有)说理方法相同吗?(相同)
三角形的中位线平行于第三边,且等于第三边的一半.说明的基本方法就是通过构造平行四边形来完成的(已学知识是在不包含基本事实:两直线被一组平行线所截,所得的对应线段成比例的前提下).

