勾画“隐圆”破解最值
李玉荣

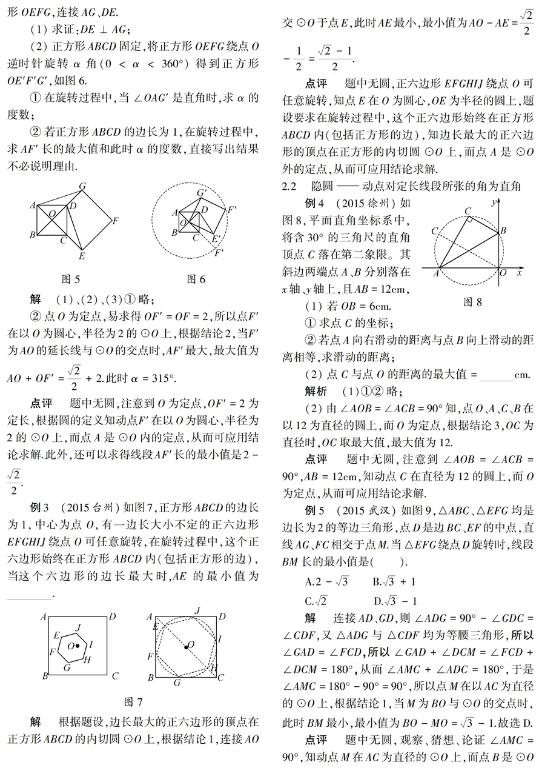
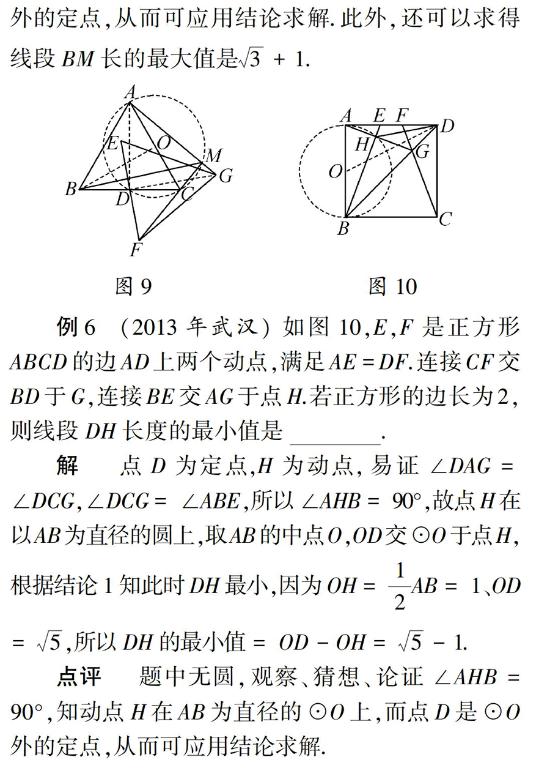
3 感悟
著名数学教育家波利亚在《怎样解题》一书中将数学解题划分为四个阶段:理解题意、拟定方案、执行方案、回顾,他在“回顾”中告诫我们:你能在别的什么题目中利用这个结果或这种方法吗?学习数学就应该在一定程度上理解其本质,掌握其方法和规律,继而会一题、解一类、通一片.最值问题既是中考的热点也是中考的难点,解决问题的策略一般为“谋定而后动”,我们看到,如果这里的“定”与圆有关,那么我们就可以“勾画”出隐圆,使图形更直观、条件更集中、解题更“圆”满,看似无关的知识由“结论”得到和谐的统一,数学之美、数学之精尽显其中.题海无边,教师要想在有限的时间内把题海中的无数条“鱼”都捕尽,再“喂”给学生,显然是不可能的,唯有授之以渔,在问题的提出与探究中,帮助学生认识数学的特点,做好知识的正迁移,善于归纳出一类题的特征,提炼出一些有价值的数学模型,使他们在学习中积累数学活动经验,在解题实践中提升自己的能力,才能把学生从题海中拉出,才能让学生以不变应万变,从容于数学学习与考试之中,减负增效的口号才可能真正得以落实.



3 感悟
著名数学教育家波利亚在《怎样解题》一书中将数学解题划分为四个阶段:理解题意、拟定方案、执行方案、回顾,他在“回顾”中告诫我们:你能在别的什么题目中利用这个结果或这种方法吗?学习数学就应该在一定程度上理解其本质,掌握其方法和规律,继而会一题、解一类、通一片.最值问题既是中考的热点也是中考的难点,解决问题的策略一般为“谋定而后动”,我们看到,如果这里的“定”与圆有关,那么我们就可以“勾画”出隐圆,使图形更直观、条件更集中、解题更“圆”满,看似无关的知识由“结论”得到和谐的统一,数学之美、数学之精尽显其中.题海无边,教师要想在有限的时间内把题海中的无数条“鱼”都捕尽,再“喂”给学生,显然是不可能的,唯有授之以渔,在问题的提出与探究中,帮助学生认识数学的特点,做好知识的正迁移,善于归纳出一类题的特征,提炼出一些有价值的数学模型,使他们在学习中积累数学活动经验,在解题实践中提升自己的能力,才能把学生从题海中拉出,才能让学生以不变应万变,从容于数学学习与考试之中,减负增效的口号才可能真正得以落实.

