中国与新加坡数学课程标准初中阶段“空间与图形”领域内容标准的比较
1 前言
新加坡是东南亚的经济强国,该国一直非常重视对国民的教育,并特别注重发挥教育的功能性和实用性的作用. 在第三次国际数学和科学评测(TIMSS)中,新加坡学生的表现一直名列前茅,这引起了国际数学教育界对该国的数学教育的重视,对她的数学教育的研究已经成为国际数学教育研究共同体的一个重要的新领域.美国教育部还专门提供资金,组织专家对此进行研究.
“空间与图形”对训练学生的逻辑思维能力有其他学科难以取代的功能,这是不容置疑的. 而逻辑思维在生活和生产实际中有广泛的应用. 因此,“空间与图形”部分的教学在初中数学教学中一直被认为是占有重要的地位的.
本研究主要是对我国2001年颁布的《全日制义务教育数学课程标准(实验稿)》(以下简称中国《标准》)(7—9年级)中的“空间与图形”部分和新加坡2006年发行的《中级数学课程提纲》(以下简称《课程提纲》)中的“几何与测量”部分的内容设置要求等进行比较研究,希望能从中探讨出一些新加坡成功的因素,从而给我国数学中“空间与图形”部分内容的教育提供一些启示.
2 比较分析
2.1 相同之处
2.1.1 重视发展学生的推理能力和交流表达能力
两种标准都注重发展学生的推理能力和交流表达能力. 如中国《标准》提出:在探索图形性质,与他人合作交流等活动过程中,发展合情推理,进一步学习有条理的思考与表达[2]. 新加坡《课程提纲》提出[1]:发展学生逻辑推理能力和数学交流表达能力,让学生能做到自主学习与合作学习相结合;数学推理,交流表达与联系能力的培养应该渗透到从小学到A水平大学的所有水平的数学学习过程中.
2.1.2 注重学生的情感体验过程
中国《标准》提到[2]:学习平移、旋转、对称的基本性质,欣赏并体验变换在现实生活中的广泛应用. 在教学中,应注重所学内容与现实生活的联系,注重使学生经历观察、操作、推理、想象等探索过程. 新加坡《课程提纲》则是这样提出:学生对数学的态度是由他们的学习经历发展形成的. 使数学学习有趣,有意义并且与生活息息相关将有助于学生形成对数学的积极态度;应注重学习活动的设计,从而加强学生对数学学习的信心和欣赏数学的态度. 由此可见,两种标准都对学生的情感体验过程给予了极大的关注. 2.2 不同之处
2.2.1 具体目标的呈现方式不同
中国《标准》在具体目标上对每一知识内容的要求都很详细,它在提出对知识点要求的方式上用了较多的“通过丰富的实例”、“结合具体例子”、和“了解”、“知道”、“理解”、“欣赏”、“体会”、 “掌握”、“探索”等词语的组合. 由这些词语,可以看到,中国《标准》对“空间与图形”的具体要求程度作了比较清楚明确的界定,因而可操作性较强,便于教师在教学实践中进行操作.
而新加坡的《课程提纲》对具体目标只是部分用到了“寻找”、“解决”这两个动词,绝大部分内容知识点只是罗列出来,却没有具体动词的. 比如,在提纲中,它只是列出了“角、三角形、勾股定理的应用”,而对这三个知识点是要求学生了解,理解还是掌握呢?它则没有说明. 可以说,新加坡的《课程提纲》在具体目标上对知识内容的要求是较为简明的,因而灵活性较强,教师在教学过程中可以根据实际情况恰当处理.
2.2.2 包含内容在广度和深度上的不同
新加坡的中学阶段开设了四种源流课程:特别课程,快捷课程,普通学术课程和普通工艺课程. 相应地它制定了三个数学课程提纲,分别是《O水准数学课程提纲》(O Level Mathematics Syllabus),主要是指导特别课程和快捷课程的数学教育;《普通学术数学课程提纲》(N(A) Level Mathematics Syllabus) ,适用于普通学术课程的数学教育和专门为普通工艺课程的数学课程而设的《普通工艺数学课程提纲》(N(T) Level Mathematics Syllabus). 由于修读特别课程和快捷课程的学生占了新加坡中学生的绝大部分,且《O水准数学课程提纲》中的内容比较全面(《普通学术数学课程提纲》和《普通工艺数学课程提纲》的内容大部分都是它的子集),因此,本文以《O水准数学课程提纲》作为新加坡《中级数学课程提纲》的代表,选择它的“几何与测量”这部分内容来与中国《标准》7—9年级的“空间与图形”这部分内容作比较.
中国《标准》中第三学段(7—9年级)的“空间与图形”部分和新加坡《O水准数学课程提纲》中的“几何与测量”部分的内容范围大致如下表1(其中新加坡《O水准课程提纲》的附加部分是不会作为直接测试内容,但有可能在平时的问题解决中需间接用到这些知识).
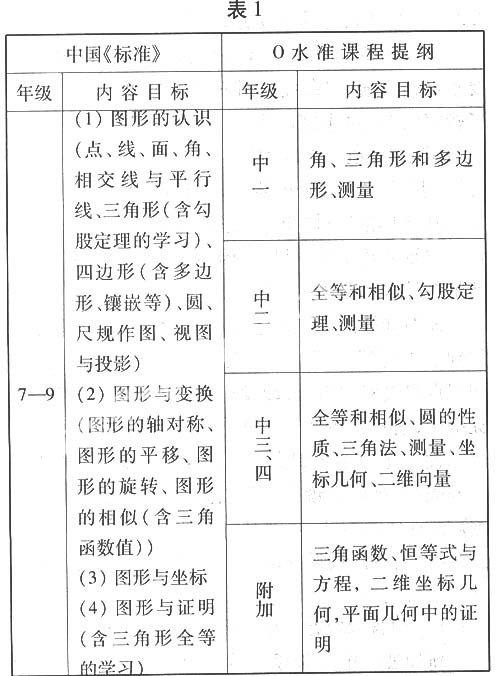
从表1可以发现,尽管中国《标准》与新加坡《O水准课程提纲》在“空间与图形”这领域内容有很多相同的知识点. 比如,角、圆、测量、图形的相似等等内容. 但在内容范围的广度上还是有不同之处的,如,“镶嵌、视图与投影、图形的平移、图形的旋转、图形与证明”等这些内容在《标准》中是有要求学习的,而《O水准课程提纲》则没有要求. 同样,“二维向量”在《O水准课程提纲》中有要求掌握,而《标准》的7—9年级则还不要求学习.
再参见《标准》(7—9年级)对“空间与图形”部分的具体要求以及《O水准课程提纲》对“几何与测量”部分内容的具体要求,详细比较研究,可以得到,中国《标准》对“空间与图形”这部分内容深度要求比新加坡的要高. 比如对相同的知识点“勾股定理”的要求来看,中国《标准》要求不仅要会应用勾股定理,还要理解体会它的证明过程. 而新加坡《O水准课程提纲》则是要求知道勾股定理并会应用它即可,要求明显低些. 再从两种标准中的不同知识内容来看,中国《标准》中要求掌握的“图形与旋转,图形与证明”等这些比较抽象,逻辑推理比较强的知识内容一直是初中生学习的难点. 而《O水准课程提纲》对 “二维向量”的学习要求不高,主要是掌握向量的一些基础概念及其基本运算.虽然《O水准课程提纲》附加部分有些内容是中国高中标准才要求学习的,但前面已经提到,附加这部分的内容是不列入学生直接考试内容的,并没有要求一定要掌握,应该可以作为学生课外学习的内容.
2.2.3 对“知识的实际应用”的要求不同
“问题解决”是新加坡中级数学课程框架的核心. [5]因而,新加坡整个数学课程的设计都是以提高学生的问题解决能力为宗旨的. 这在《课程提纲》对“几何与测量”部分的要求也可以体现出来,例如,“应用全等和相似解决简单的实际问题”,“测量球体,圆锥等的体积“,”通过测量,结合所学知识解决实际生活中一些组合体的体积和表面积问题”等等. 中国《标准》在“空间与图形”这部分内容中也有提出要学生“运用三角函数解决与直角三角形有关的简单实际问题”的要求,但总体上来看,强调要求不够突出,重视程度没有新加坡的高.
3 启示
通过两种标准的比较可知,新加坡《课程提纲》要求中学4年所学习的“空间与图形”这领域内容并不比中国初中生三年要学习的内容多很多,反而学的知识相对简单. 可见,新加坡数学教育是比较注重巩固学生的基础知识的. 文[6]对新加坡数学教材中的“勾股定理”这节内容的分析,也得到这个特点. 而且新加坡的《课程提纲》对“推理证明”不作过多要求,它更多的是关注学生对知识的实际应用.
笔者认为,在数学课程改革中,我们应该向新加坡学习,在保持我国“注重双基教学”的优良传统基础上,淡化演绎推理证明,注重知识的实际应用. 记得“新课标”刚颁布时,曾有专家指出:“‘新课标大大淡化了数学中的推理证明,会使数学课失去灵魂. ”推理证明可以锻炼学生的逻辑思维能力,这是无可厚非的. 但淡化并不等于没有,只是旧课程要求的证明过多过繁,不利于学生的全面发展,所以我们应该将要求降低. 至于“关注知识的应用”方面,我们知道,“学以致用”一直是我们教育所追求的重要目标之一,因而,在我们的数学教学过程中应加强与解决实际问题的联系. 在“空间与图形”部分的教学更应该与实际测量等一些日常生活活动结合起来进行.
当然,数学教育的成功,不仅需要制定合适的数学课程标准,还需要编制出恰当的数学教材以及选取有效的数学教学方法等相结合. 因此,我们可以进一步去探究新加坡数学教材,教法方面的优点与不足,从而为我国的数学教育提供更多的参考与借鉴.
参考文献
[1] Ministry of Education .Singapore.Secondary Mathematics Syllabuses[M].2007.
[2] 中华人民共和国教育部,全日制义务教育数学课程标准(实验稿)[M].北京:北京师范大学出版社,2007.37-50.
[3] 李秉彝,江春莲.新的O水准数学大纲之新体现在何处[J].数学通报,2007,46(9): 7-9.
[4] 刘长明,孙连举.中美两国数学课程标准中初中学段“空间与图形”领域的内容标准之比较[J].数学教育学报,2002,11(4):49-51.
[5] 黄翔,童莉.新加坡的新数学教材《New Mathematics Counts》[J].数学通报,2003,(11):29-32.
[6] 朱哲.新加坡数学教材中的“勾股定理”[J]. 数学教学,2008,(4):4-15.
作者简介 余小兰,女,1985年2月生,广东高州人.华南师范大学2008级4+2教师教育硕士研究生,主要研究方向是数学教育理论.
新加坡是东南亚的经济强国,该国一直非常重视对国民的教育,并特别注重发挥教育的功能性和实用性的作用. 在第三次国际数学和科学评测(TIMSS)中,新加坡学生的表现一直名列前茅,这引起了国际数学教育界对该国的数学教育的重视,对她的数学教育的研究已经成为国际数学教育研究共同体的一个重要的新领域.美国教育部还专门提供资金,组织专家对此进行研究.
“空间与图形”对训练学生的逻辑思维能力有其他学科难以取代的功能,这是不容置疑的. 而逻辑思维在生活和生产实际中有广泛的应用. 因此,“空间与图形”部分的教学在初中数学教学中一直被认为是占有重要的地位的.
本研究主要是对我国2001年颁布的《全日制义务教育数学课程标准(实验稿)》(以下简称中国《标准》)(7—9年级)中的“空间与图形”部分和新加坡2006年发行的《中级数学课程提纲》(以下简称《课程提纲》)中的“几何与测量”部分的内容设置要求等进行比较研究,希望能从中探讨出一些新加坡成功的因素,从而给我国数学中“空间与图形”部分内容的教育提供一些启示.
2 比较分析
2.1 相同之处
2.1.1 重视发展学生的推理能力和交流表达能力
两种标准都注重发展学生的推理能力和交流表达能力. 如中国《标准》提出:在探索图形性质,与他人合作交流等活动过程中,发展合情推理,进一步学习有条理的思考与表达[2]. 新加坡《课程提纲》提出[1]:发展学生逻辑推理能力和数学交流表达能力,让学生能做到自主学习与合作学习相结合;数学推理,交流表达与联系能力的培养应该渗透到从小学到A水平大学的所有水平的数学学习过程中.
2.1.2 注重学生的情感体验过程
中国《标准》提到[2]:学习平移、旋转、对称的基本性质,欣赏并体验变换在现实生活中的广泛应用. 在教学中,应注重所学内容与现实生活的联系,注重使学生经历观察、操作、推理、想象等探索过程. 新加坡《课程提纲》则是这样提出:学生对数学的态度是由他们的学习经历发展形成的. 使数学学习有趣,有意义并且与生活息息相关将有助于学生形成对数学的积极态度;应注重学习活动的设计,从而加强学生对数学学习的信心和欣赏数学的态度. 由此可见,两种标准都对学生的情感体验过程给予了极大的关注. 2.2 不同之处
2.2.1 具体目标的呈现方式不同
中国《标准》在具体目标上对每一知识内容的要求都很详细,它在提出对知识点要求的方式上用了较多的“通过丰富的实例”、“结合具体例子”、和“了解”、“知道”、“理解”、“欣赏”、“体会”、 “掌握”、“探索”等词语的组合. 由这些词语,可以看到,中国《标准》对“空间与图形”的具体要求程度作了比较清楚明确的界定,因而可操作性较强,便于教师在教学实践中进行操作.
而新加坡的《课程提纲》对具体目标只是部分用到了“寻找”、“解决”这两个动词,绝大部分内容知识点只是罗列出来,却没有具体动词的. 比如,在提纲中,它只是列出了“角、三角形、勾股定理的应用”,而对这三个知识点是要求学生了解,理解还是掌握呢?它则没有说明. 可以说,新加坡的《课程提纲》在具体目标上对知识内容的要求是较为简明的,因而灵活性较强,教师在教学过程中可以根据实际情况恰当处理.
2.2.2 包含内容在广度和深度上的不同
新加坡的中学阶段开设了四种源流课程:特别课程,快捷课程,普通学术课程和普通工艺课程. 相应地它制定了三个数学课程提纲,分别是《O水准数学课程提纲》(O Level Mathematics Syllabus),主要是指导特别课程和快捷课程的数学教育;《普通学术数学课程提纲》(N(A) Level Mathematics Syllabus) ,适用于普通学术课程的数学教育和专门为普通工艺课程的数学课程而设的《普通工艺数学课程提纲》(N(T) Level Mathematics Syllabus). 由于修读特别课程和快捷课程的学生占了新加坡中学生的绝大部分,且《O水准数学课程提纲》中的内容比较全面(《普通学术数学课程提纲》和《普通工艺数学课程提纲》的内容大部分都是它的子集),因此,本文以《O水准数学课程提纲》作为新加坡《中级数学课程提纲》的代表,选择它的“几何与测量”这部分内容来与中国《标准》7—9年级的“空间与图形”这部分内容作比较.
中国《标准》中第三学段(7—9年级)的“空间与图形”部分和新加坡《O水准数学课程提纲》中的“几何与测量”部分的内容范围大致如下表1(其中新加坡《O水准课程提纲》的附加部分是不会作为直接测试内容,但有可能在平时的问题解决中需间接用到这些知识).

从表1可以发现,尽管中国《标准》与新加坡《O水准课程提纲》在“空间与图形”这领域内容有很多相同的知识点. 比如,角、圆、测量、图形的相似等等内容. 但在内容范围的广度上还是有不同之处的,如,“镶嵌、视图与投影、图形的平移、图形的旋转、图形与证明”等这些内容在《标准》中是有要求学习的,而《O水准课程提纲》则没有要求. 同样,“二维向量”在《O水准课程提纲》中有要求掌握,而《标准》的7—9年级则还不要求学习.
再参见《标准》(7—9年级)对“空间与图形”部分的具体要求以及《O水准课程提纲》对“几何与测量”部分内容的具体要求,详细比较研究,可以得到,中国《标准》对“空间与图形”这部分内容深度要求比新加坡的要高. 比如对相同的知识点“勾股定理”的要求来看,中国《标准》要求不仅要会应用勾股定理,还要理解体会它的证明过程. 而新加坡《O水准课程提纲》则是要求知道勾股定理并会应用它即可,要求明显低些. 再从两种标准中的不同知识内容来看,中国《标准》中要求掌握的“图形与旋转,图形与证明”等这些比较抽象,逻辑推理比较强的知识内容一直是初中生学习的难点. 而《O水准课程提纲》对 “二维向量”的学习要求不高,主要是掌握向量的一些基础概念及其基本运算.虽然《O水准课程提纲》附加部分有些内容是中国高中标准才要求学习的,但前面已经提到,附加这部分的内容是不列入学生直接考试内容的,并没有要求一定要掌握,应该可以作为学生课外学习的内容.
2.2.3 对“知识的实际应用”的要求不同
“问题解决”是新加坡中级数学课程框架的核心. [5]因而,新加坡整个数学课程的设计都是以提高学生的问题解决能力为宗旨的. 这在《课程提纲》对“几何与测量”部分的要求也可以体现出来,例如,“应用全等和相似解决简单的实际问题”,“测量球体,圆锥等的体积“,”通过测量,结合所学知识解决实际生活中一些组合体的体积和表面积问题”等等. 中国《标准》在“空间与图形”这部分内容中也有提出要学生“运用三角函数解决与直角三角形有关的简单实际问题”的要求,但总体上来看,强调要求不够突出,重视程度没有新加坡的高.
3 启示
通过两种标准的比较可知,新加坡《课程提纲》要求中学4年所学习的“空间与图形”这领域内容并不比中国初中生三年要学习的内容多很多,反而学的知识相对简单. 可见,新加坡数学教育是比较注重巩固学生的基础知识的. 文[6]对新加坡数学教材中的“勾股定理”这节内容的分析,也得到这个特点. 而且新加坡的《课程提纲》对“推理证明”不作过多要求,它更多的是关注学生对知识的实际应用.
笔者认为,在数学课程改革中,我们应该向新加坡学习,在保持我国“注重双基教学”的优良传统基础上,淡化演绎推理证明,注重知识的实际应用. 记得“新课标”刚颁布时,曾有专家指出:“‘新课标大大淡化了数学中的推理证明,会使数学课失去灵魂. ”推理证明可以锻炼学生的逻辑思维能力,这是无可厚非的. 但淡化并不等于没有,只是旧课程要求的证明过多过繁,不利于学生的全面发展,所以我们应该将要求降低. 至于“关注知识的应用”方面,我们知道,“学以致用”一直是我们教育所追求的重要目标之一,因而,在我们的数学教学过程中应加强与解决实际问题的联系. 在“空间与图形”部分的教学更应该与实际测量等一些日常生活活动结合起来进行.
当然,数学教育的成功,不仅需要制定合适的数学课程标准,还需要编制出恰当的数学教材以及选取有效的数学教学方法等相结合. 因此,我们可以进一步去探究新加坡数学教材,教法方面的优点与不足,从而为我国的数学教育提供更多的参考与借鉴.
参考文献
[1] Ministry of Education .Singapore.Secondary Mathematics Syllabuses[M].2007.
[2] 中华人民共和国教育部,全日制义务教育数学课程标准(实验稿)[M].北京:北京师范大学出版社,2007.37-50.
[3] 李秉彝,江春莲.新的O水准数学大纲之新体现在何处[J].数学通报,2007,46(9): 7-9.
[4] 刘长明,孙连举.中美两国数学课程标准中初中学段“空间与图形”领域的内容标准之比较[J].数学教育学报,2002,11(4):49-51.
[5] 黄翔,童莉.新加坡的新数学教材《New Mathematics Counts》[J].数学通报,2003,(11):29-32.
[6] 朱哲.新加坡数学教材中的“勾股定理”[J]. 数学教学,2008,(4):4-15.
作者简介 余小兰,女,1985年2月生,广东高州人.华南师范大学2008级4+2教师教育硕士研究生,主要研究方向是数学教育理论.

