基于图形计算器开展高中数学实验探索

    李峰 高学

    

    

    

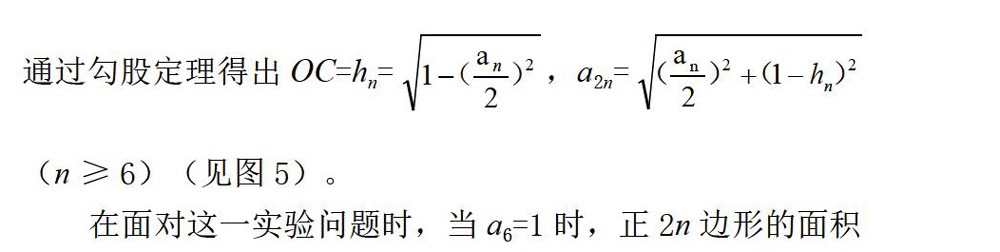
    摘? 要 图形计算器被称为移动的数学实验室，为学生动手操作实验学习数学，提供了极大的便利。从教学实践出发，对基于图形计算器的高中数学实验进行探索，以期为一线教学提供参考和帮助。

    关键词 图形计算器;高中数学;数学实验;核心素养

    中图分类号：G633.6? ? 文献标识码：B

    文章编号：1671-489X（2020）07-0123-03

    1 前言

    《普通高中数学课程标准》提出，学生需要具备六大核心素养，分别是数学抽象、数据分析、数学建模、数据运算、直观想象。图形计算器的出现，为学生的数学核心素养培养提供了保障。借助图形计算器，学生可以自主进行观察、操作、分析、比较。为此，在今后的高中数学教学中，教师有必要对基于图形计算器开展数学实验进行更加深入的探索。

    2 基于图形计算器的曲边图形面积实验

    “曲边图形面积”是高中数学教学中比较有代表性的数学实验。在这一数学实验中，图形计算器的运用，可为学生的实验学习创造便利。笔者举这样一个例子：

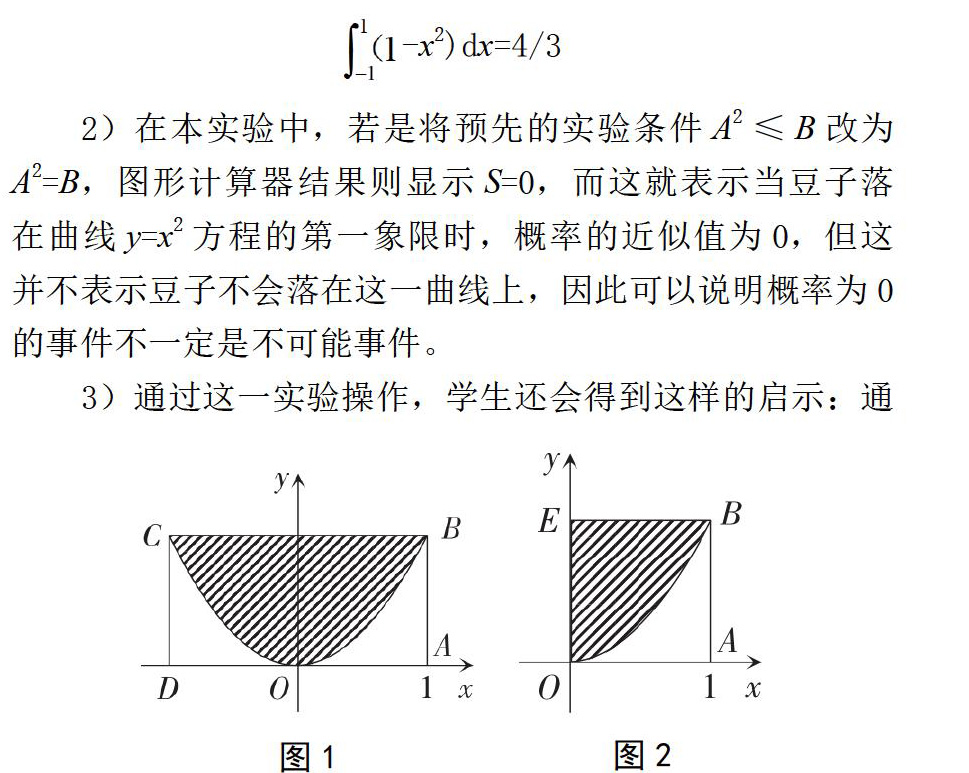
    向长方形ABCD区域内随机撒N粒豆子（假设每一粒豆子都可以落到长方形区域内。同时，阴影区域内豆子数只与区域大小有关，与区域位置形状无关），试问如何求概率P？具体详见图1。

    在面对这一问题时，学生很容易想到用豆子落在阴影区域内的频率表示概率，这样这一实验问题就被转换为“如何求豆子落在阴影区域内的频率”。此时学生就会有這样的猜想，即通过“撒豆子”实验，通过对实验数据的记录，将频率“数出来”。但是很显然，这一实验操作是存在一定困难的，不仅操作过程烦琐，还容易出现记录错误问题。此时，图形计算器就成为学生实验中可借助的工具。

    如在笔者执教的班级中，通过学生之间的相互讨论合作，做出基于图形计算器的“曲边图形面积”实验方案设计：

    1）借助图形计算器工具，在[-1，1]和[0，1]区域之间，选取两个随机数A和B，并构建坐标点（A，B）代替实验操作中的豆子;

    2）若是选取的点（A，B）满足A2≤B的实验条件，就表示撒落的豆子落到了阴影区域内;

    3）在完成操作“撒落N个豆子”的实验过程中，统计落在阴影区域中的豆子数，并将其记做K;

    4）使用落在阴影区域内的“豆子”的频率作为概率，通过K/N≈S阴影/S矩形ABCD，从而得出关系式S阴影≈K/N×S矩形ABCD=2K/N[1]。

    上述提及的问题被学生圆满解决。但由于这一实验操作还存在一定的困难，为此在实验教学过程中，教师可以对学生做进一步的引导，让学生试想还有没有更为简单的实验方法并大胆提出来。通过深入思考，又有学生提出实验方案，具体流程步骤如下。

    1）由于图形计算器工具可直接产生[0，1]区域随机数，这样就可以将原图的阴影面积转化为图2阴影面积乘以2。

    2）利用图形计算器工具图形绘制功能，就可以对正方形ABEO和落在区域阴影面积的点（A，O）进行绘制，从而使“撒落N个豆子”的实验过程变得更加形象直观。

    3）利用图形计算器工具中的内部程序模式，将上述提及的步骤方案编制成特定的程序，这样图形计算器工具就可以进行自动化的实验操作，具体如图3所示。

    通过上述实验，学生可以得出几种结论。

    1）当豆子数N为500时，程序结果为阴影部分面积的估计值（即x=1，y=x2围成的面积），这样当N被不断放大时，面积的近似值就会无限接近4/3，由此就可以得出：

    2）在本实验中，若是将预先的实验条件A2≤B改为A2=B，图形计算器结果则显示S=0，而这就表示当豆子落在曲线y=x2方程的第一象限时，概率的近似值为0，但这并不表示豆子不会落在这一曲线上，因此可以说明概率为0的事件不一定是不可能事件。

    3）通过这一实验操作，学生还会得到这样的启示：通过几何概型、随机模拟的方式，可以对近似不规则的曲线图形面积进行计算。借助图形计算器工具，使复杂的“曲线图形面积”计算变得简单，彰显出图形计算器在高中数学实验教学中的应用价值。

    3 基于图形计算器的概率实验

    概率是学生在高中阶段学习的重要数学知识，为更好地帮助学生加深对概率知识的理解，实验操作是不可或缺的。而与概率有关的数学实验就可以利用图形计算器开展。以探究班级中学生两人生日在同一天的概率为例，在实验开展前，教师可以通过导入：“我们班有50名学生，老师相信你们其中一定有至少两人生日是同一天的。”很多学生表示不相信，认为这样的概率非常小。而此时教师就可以趁机引导学生：愿不愿意通过实验操作的方式，否定老师提出的想法？此时学生实验学习探究的积极性被调动，并积极踊跃地参与到实验探究中来。

    在班级学生探究思考过程中，有学生提出这样的想法：“班级同学生日的结果是有限的，可在任何一天，因此，这一实验问题符合古典概型条件，可将其视作古典概型问题。”在这一猜想下，就有学生进一步指出可采用投硬币的实验方式，去进行班级中学生两人生日在同一天的概率实验。如可以进行数据调查，把班级学生的生日都统计一遍，就可以得到该事件发生的频率。这样的实验方案的确是可行的，但问题是操作较为麻烦。对此，教师可以引导学生：是否可以使用图形计算器设计更为简单的实验方案？在这样的引导下，就有学生做出实验设计，具体步骤如下。

    1）将[1，365]作为N个随机数的产生区间，并以此代表班级所有学生的生日。

    2）在N个随机数中，若是有相邻的两个数相同，那么就表示班级之中有至少两个学生的生日是相同的，这样就可以验证实验的猜想，并将其记为K+1。

    3）使用图形计算器重复进行这样的实验操作M次，最后记录实验成功的次数K，并与实验操作次数M进行比值计算，所得到的最终数据就为班级中学生两人生日在同一天的概率。

    利用图形计算器工具中的内部程序模式，将上述提及的步骤方案编制成特定的程序，这样图形计算器工具就可以进行自动化实验操作，具体如图4所示。

    而通过上述实验，学生可以得出以下结论。

    1）假设该实验进行200次操作，即M=200，图形计算器显示结果，若是一个班级中的学生人数超过24人，班级中学生两人生日在同一天的概率要超过此次事件不可能发生的概率;而若是班级中的学生人数超出40人，则此事件的发生概率有90%的可能;而若是班级中的学生人数超过50人，那么这一事件则一定可能发生，因此，教师所作出的假设猜想是对的。

    2）实验操作次数M不断增加，事件发生的频率就会越趋近于概率，其中P=。

    4 基于图形计算器的割圆术验证实验

    割圆术是中国古代数学家提出的一种求圆周率的猜想算法，最早是由魏晋时期的数学家刘徽提出的（公元263年），主要是通过圆内接正六边形的方式，无限地进行分割，从而最大限度地趋于接近圆的面积，这样就可以获得圆周率。其后，南北朝时期著名数学家祖冲之进一步对割圆术进行研究，并将圆周率精确到小数点后七位，而这一演算结果是早于欧洲的，足以证明我国古代数学家的智慧[2]。

    在古代，由于条件的限制，割圆术还只是一种猜想;但在当下，尤其是随着图形计算器的出现，只需要输入相关的数据，就可以进行自动化的分割操作。这为数学实验教学创造了极大的便利，同时可以进一步帮助学生认识数学文化价值，促使学生的数学核心素养得到有效培养。笔者在执教过程中就曾从割圆术出发，为学生布置相关的实验任务，并引导学生使用图形计算器工具探索解决。

    然后，教师可以带领全体学生对π的数学模型计算公式进行分析，并使用循环的术语进行表达，学生就会发现割圆术计算的是圆内接正六边形、内接正十二边形……内接正n边形可表示为6×2N。然后利用图形计算器工具中的内部程序模式，将上述提及的步骤方案编制成特定的程序，就可以得到最终的实验结果，具体如图6所示。

    而通过上述实验，学生可以得出如下结论。

    1）当设定N=5时，圆内接正多边形数可达到192，这样可以得到π=3.14，就得到數学家刘徽得出的计算结果，即“徽率”。而当圆内正接多边形达到24 576时，就可以得到π=3.141 592 6，这是祖冲之计算出的圆周率。现下使用图形计算器，很轻松地得出这样的计算结果，但是早在千百年前，在计算工具极为简陋的情况下，我国的数学家可以得到这样的计算结果，体现了我国古代先进的数学水平。

    2）当圆的内接正多边形无限逼近于圆的面积时，圆的外接多边形的周长也越趋于圆的周长，而这是古希腊数学家阿基米德提出的穷竭法。借助图形计算器，对割圆术与穷竭法进行比较，是中外数学文化研究智慧碰撞的体现。

    5 结语

    图形计算器在高中数学教学中的应用是教学现代化的重要体现，符合课程标准提出的“信息技术与数学课程深度融合”的要求。学生在手持使用图形计算器的过程中，在做中学习数学知识，这就为教学效率的提升及学生数学核心素养的培养发展提供了保障。为此，在今后的高中数学教学中，教师应对基于图形计算器的数学实验开展进行深入探索。

    参考文献

    [1]高鹏，李师师，常磊.基于图形计算器开展高中数学实验探索[J].中国数学教育：高中版，2019（1）：11-14.

    [2]陆高平.利用图形计算器开展数学实验的实践探索[J].数学之友，2016（8）：69-70.