代数教学中不要以“形”代“数”
翟立安
上海二期课改数学新教材(试验本)在初中代数的编排上有一个显著特点,就是让代数教学从过去的“无形”走向现在的“有形”,这样的编排是为了降低代数教学的抽象性,通过以“形”助“数”让学生更加直观地理解代数运算法则的合理性,搭起“脚手架”,增加“有意义”学习的成分.
遗憾的是,在教学现实中个别老师曲解了这样编排的意图,而是以“形”代“数”了.
请看下面的教学片段(上海教育出版社七年级第一学期数学(试验本)“多项式与多项式的乘法”第1课时).
[教学片段]
预备铃后,Z老师在黑板上画出右图.
师问:整式包括哪两部分?
学生1:单项式与多项式.
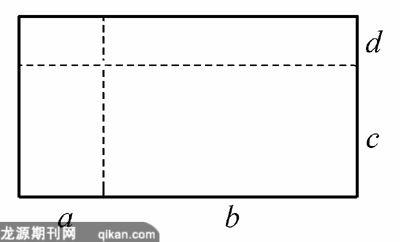
老师接着问:如图矩形的面积是什么?
学生2:S=(a+b)·(c+d).
师说:这里边长是多项式,多项式乘以多项式,我们还不会算,今天就学习多项式与多项式相乘. 以前我们学习过单项式乘单项式、单项式乘多项式,用学过的知识来解决新问题. 我们将矩形分割,分割后有没有其它方法求它的面积呢?
生3:求四个小长方形的面积,所以S=ac+bc+ad+bd.
师问:这两个是不是相等的?
学生齐答:是.
师问:还有那些方法?
生4:用上下或左右两块面积计算,S=a(c+d)+b(c+d)
师问::这是单项式与多项式相乘,结果就是ac+ad+bc+bd. 那么S=(a+b)·(c+d)等于什么?
生5:先把(a+b)看成一个整体.
老师打断:没关系,你就直接说结果吧!
生6:(a+b)·(c+d)=ac+ad+bc+bd.
师:好,我们得到了多项式与多项式的乘法法则.
听到这里,我的脑海里升起一朵又一朵疑问的浪花.
1.研究多项式与多项式的乘法,怎么一开始就想到画分割好的矩形?
2.用几种不同的方法计算一个具体的矩形面积,通过面积相等就得到了多项式与多项式的乘法法则,这样一来多项式中的字母岂不只限于正数(边长)了?
3.一个具体的几何(面积)计算能代替一般的严格意义的逻辑推导(证明)?
4.学生说“先把(a+b)看成一个整体”,说得多好,老师为什么打断他?
可见,这样的教学设计不但生硬,而且漏洞百出!
数学有自己的文化本质,代数有自己的逻辑体系,它不能靠“形象”替自己说话,只能借助“形象”来思考、阐述和解释.
那么,代数教学中怎样用好“形象”来促进“抽象”而不是代替“抽象”呢?
就这个问题,我帮Z老师重新进行了教学设计.
[教学片段]
首先,给出5条单项式乘单项式、单项式乘多项式的小练习.
师:比一比,看谁做得又快又好. (学生的注意力一下子集中起来)
几分钟的时间进行交流,交流的过程中复习单项式乘单项式、单项式乘多项式的重点和注意事项.
师问:m(a+b)=?
生齐答:m(a+b)=ma+mb,(1)
师问:如果把m换成式子(c+d)又怎么计算?
生1:(c+d)·(a+b)=(ac+cb)+(cb+db). (显然这里有误)
师:你是怎么得来的?
生:代进去的.
师:你代到(1)式再试试!
生1:m(a+b)=ma+mb=(c+d)a+(c+d)b=ac+ad+bc+bd
(学生发现错误)
师:这里的m是多项式(c+d),我们得到了多项式与多项式相乘的结果.
接着,老师说:我遇到一个困惑,有一个边长分别为a米、b米的长方形,长和宽分别增加m米、n米,问现在的长方形的面积是多少?请把变化后的图画出来.
学生有不同的画法,也得出面积的不同表示式.
有直接计算的:S=(a+m)·(b+n);
有分为三块的:S=(b+n)·m+an+ab;
有分为四块的:S=mn+an+bm+ab.
师:看一下,用不同方式表示的同一个矩形的面积,它们应该是相等的!
(a+m)·(b+n)=mn+an+bm+ab,所以我们又得到了多项式乘多项式的结果. 它们的形式是完全一样的!
师:看来,无论是从整体思想进行代数推导,还是从几何角度进行验证,多项式乘多项式的结果都是一样的. 请用文字来表达多项式乘多项式的运算法则.
生沉默.
老师给一点提示:类似于以前单项式乘多项式的.
学生纷纷尝试.
一学生表达,老师帮助完善,得到多项式乘多项式的法则.
师:这里的字母a、b、m、n可以是数,也可以是代数式.
学生齐读一遍教材上多项式乘多项式的法则后,进入练习阶段.
从上面教学设计的改进以及教学的实际效果,我们可以看到:代数教学中不是用粗糙的“形象”代替严格的代数推导,而是借用“形象”启迪学生思维或进行验证阐述等,以让学生更容易认同和理解.
可见,代数教学中一定要处理好“形象思考”与“抽象思维”的辩证关系!
上海二期课改数学新教材(试验本)在初中代数的编排上有一个显著特点,就是让代数教学从过去的“无形”走向现在的“有形”,这样的编排是为了降低代数教学的抽象性,通过以“形”助“数”让学生更加直观地理解代数运算法则的合理性,搭起“脚手架”,增加“有意义”学习的成分.
遗憾的是,在教学现实中个别老师曲解了这样编排的意图,而是以“形”代“数”了.
请看下面的教学片段(上海教育出版社七年级第一学期数学(试验本)“多项式与多项式的乘法”第1课时).
[教学片段]
预备铃后,Z老师在黑板上画出右图.
师问:整式包括哪两部分?
学生1:单项式与多项式.

老师接着问:如图矩形的面积是什么?
学生2:S=(a+b)·(c+d).
师说:这里边长是多项式,多项式乘以多项式,我们还不会算,今天就学习多项式与多项式相乘. 以前我们学习过单项式乘单项式、单项式乘多项式,用学过的知识来解决新问题. 我们将矩形分割,分割后有没有其它方法求它的面积呢?
生3:求四个小长方形的面积,所以S=ac+bc+ad+bd.
师问:这两个是不是相等的?
学生齐答:是.
师问:还有那些方法?
生4:用上下或左右两块面积计算,S=a(c+d)+b(c+d)
师问::这是单项式与多项式相乘,结果就是ac+ad+bc+bd. 那么S=(a+b)·(c+d)等于什么?
生5:先把(a+b)看成一个整体.
老师打断:没关系,你就直接说结果吧!
生6:(a+b)·(c+d)=ac+ad+bc+bd.
师:好,我们得到了多项式与多项式的乘法法则.
听到这里,我的脑海里升起一朵又一朵疑问的浪花.
1.研究多项式与多项式的乘法,怎么一开始就想到画分割好的矩形?
2.用几种不同的方法计算一个具体的矩形面积,通过面积相等就得到了多项式与多项式的乘法法则,这样一来多项式中的字母岂不只限于正数(边长)了?
3.一个具体的几何(面积)计算能代替一般的严格意义的逻辑推导(证明)?
4.学生说“先把(a+b)看成一个整体”,说得多好,老师为什么打断他?
可见,这样的教学设计不但生硬,而且漏洞百出!
数学有自己的文化本质,代数有自己的逻辑体系,它不能靠“形象”替自己说话,只能借助“形象”来思考、阐述和解释.
那么,代数教学中怎样用好“形象”来促进“抽象”而不是代替“抽象”呢?
就这个问题,我帮Z老师重新进行了教学设计.
[教学片段]
首先,给出5条单项式乘单项式、单项式乘多项式的小练习.
师:比一比,看谁做得又快又好. (学生的注意力一下子集中起来)
几分钟的时间进行交流,交流的过程中复习单项式乘单项式、单项式乘多项式的重点和注意事项.
师问:m(a+b)=?
生齐答:m(a+b)=ma+mb,(1)
师问:如果把m换成式子(c+d)又怎么计算?
生1:(c+d)·(a+b)=(ac+cb)+(cb+db). (显然这里有误)
师:你是怎么得来的?
生:代进去的.
师:你代到(1)式再试试!
生1:m(a+b)=ma+mb=(c+d)a+(c+d)b=ac+ad+bc+bd
(学生发现错误)
师:这里的m是多项式(c+d),我们得到了多项式与多项式相乘的结果.
接着,老师说:我遇到一个困惑,有一个边长分别为a米、b米的长方形,长和宽分别增加m米、n米,问现在的长方形的面积是多少?请把变化后的图画出来.
学生有不同的画法,也得出面积的不同表示式.
有直接计算的:S=(a+m)·(b+n);
有分为三块的:S=(b+n)·m+an+ab;
有分为四块的:S=mn+an+bm+ab.
师:看一下,用不同方式表示的同一个矩形的面积,它们应该是相等的!
(a+m)·(b+n)=mn+an+bm+ab,所以我们又得到了多项式乘多项式的结果. 它们的形式是完全一样的!
师:看来,无论是从整体思想进行代数推导,还是从几何角度进行验证,多项式乘多项式的结果都是一样的. 请用文字来表达多项式乘多项式的运算法则.
生沉默.
老师给一点提示:类似于以前单项式乘多项式的.
学生纷纷尝试.
一学生表达,老师帮助完善,得到多项式乘多项式的法则.
师:这里的字母a、b、m、n可以是数,也可以是代数式.
学生齐读一遍教材上多项式乘多项式的法则后,进入练习阶段.
从上面教学设计的改进以及教学的实际效果,我们可以看到:代数教学中不是用粗糙的“形象”代替严格的代数推导,而是借用“形象”启迪学生思维或进行验证阐述等,以让学生更容易认同和理解.
可见,代数教学中一定要处理好“形象思考”与“抽象思维”的辩证关系!

