如此开门见山要不得
教学案情
下面是八年级数学第二学期三角形中位线教学中的一个教学片段:
……
师:这一节课我们一起研究三角形中位线.
师:首先我们给三角形中位线下个定义.
(边写边说:连接三角形两边中点的线段叫做三角形中位线. )
师:请同学们画出三角形的所有中位线.
(同学们迅速拿出纸和笔,认真的画起来. )
师:请问三角形共有几条中位线?
生1:三条.
生2:一条.
师:到底有几条呢?
大部分学生高声回答:3条.
师:回答得很好!三角形的中位线共有三条,并且三角形的中位线具有很重要的性质.
板书:三角形中位线定理 三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
师:下面,我们利用三角形中位线定理来解决一些题目.
……
诊断分析
作为听课教师,我们都有一种感觉:执教者开门见山,平铺直叙,直现主题,好像在追赶即将到站的班车. 对于新知识,学生犹如雾里看花,水中望月,没有了理解和摸索,缺少了反思和探究. 纵观这一教学片段,我认为至少存在以下几个方面的问题:
一、教学内容偏离了大纲要求
教材对三角形中位线的三维目标是:(1)知识与技能:使学生理解三角形中位线的概念,掌握三角形中位线定理,同时要会用三角形中位线定理进行有关的论证和计算;(2)过程与方法:培养学生动手动脑、发现问题、解决问题的能力;(3)情感、态度及价值观:对学生进行实践——认识——实践的辩证唯物主义认识论教育. 显然,在这教学过程中,学生只能被动的接受知识,没有了观察、猜测、实验. 课堂充满了教师填鸭式的灌输,没有了问题指向. 希伯特等人指出:“问题为本学习所指的,不仅是在以学科为中心的课程中加入一些问题解决活动,更是构想课程的一种方法”. 可见,本课设计不合理,无法达到“为学习设计课堂”. (加涅语)
另外,教材上在三角形中位线定理的证法中,利用了数学中的化归思想,这正是学生的薄弱环节. 根据本节课的内容和学生的实际水平,宜采用的是引导发现法和直观演示法. 在引出三角形中位线定理后,通过投影仪进行教具的直观演示,引导启发学生,让学生理解线段间的倍分问题,最终可以化归为我们很熟悉的线段相等问题.通过演示,使学生在获得感性知识的同时,为掌握理性知识创造条件.这样做,符合教学论中的直观性和可接受性原则.
二、教学导入远离了生活实际
开门见山地引如主题,本无可厚非,但就三角形中位线这一内容与我们的生活息息相关,数学教学生活化是时下较为流行的提法与做法,因此,教学设计中,可以通过解决测量河宽、建筑物高度等问题引入新课,毕竟,数学情境是联系数学与现实的纽带,是沟通数学与现实生活的桥梁. 通过实际问题让学生认识中位线定理的现实意义,加深对中位线定理的理解. 通过数学模型与生活实例挂钩,促进学生主动为解决问题而探索三角形中位线运用原理,唤醒学生参与意识,让数学知识因贴近生活而变得有趣,使学生领悟数学“源于生活、又用于生活”的道理,从而更主动地投入学习、探索之中.
三、教学过程忽视了思想生成
三角形中位线定理内容简洁,但不应淡化其生成过程. 新课标指出,课堂教学要重视知识的形成过程,包括渗透知识的文化背景、实际应用背景等,这些能大大激发学生对知识的好奇性,并积极主动地参与教学活动;让学生作出三角形的所有中位线(3条),不仅可以让学生更清楚地认识中位线,而且在不知不觉中分化了这节课的难点,并为下面找中位线与第三边的数量、位置关系作好了准备. 但是,在生2回答错误的情况下,教师一带而过,缺少了师生、生生之间的有效交流与平等对话,活生生的拔掉了学生知识网络建构的桩基. 三角形中位线生成有多种途径、多种方法,教师缺少了引领,没有重点突出某种生成过程.
四、教学方法漠视了数学实验
三角形中位线定理是初中几何的一个重要知识内容. 就事论事,只能让学生学会死搬硬套,而且只是暂时性的掌握内容,无法真正实现学数学、用数学的目的. 数学实验是指为研究或获得某种数学结论,验证某种数学猜想,实验者运用一定的方法,在特定的实验条件下所进行的一种数学探究活动,其目的是引导学生参与实践、自主探索、合作交流. 在三角形中位线定理的引入上,教师没有为学生提供和创设以数学实验为情境的数学问题,无法培养学生的数学实验技能,没有为学生猜想保驾护航,丧失了提升学生创新、创造能力的机会.
实际操作时,可以通过“回忆——作图——设疑——探索——发现——论证”而让学生掌握三角形中位线与第三边的数量关系和位置关系,并且对教材中的论证方法有了较深的印象,从而突破本节课的难点.
结合教学实情,笔者认为可以从以下几个方面进行改进:
1.重视导入方式的开放性,激发学生自主学习
恰当适时的课堂导入可激发学生的学习兴趣,产生学习动机,引起学生对所学课题的关注,传达教学意图,为学习新知识、新概念和新技能做鼓动和铺垫. 良好的开端是成功的一半. 上课伊始,教师可先提出下列问题:有一个池塘岸边设有两观测点,不能直接到达,现需要在它们之间接一电话线,请你设法测出它们之间的距离. 思维永远是从问题开始的. 教学过程是一个提出问题和解决问题的持续不断的活动,只要教师有意识地设计出悬念,就能从“悬”中激发学生的求知欲,吸引学生的注意力,学生就会产生“愿闻其详”的心情. 这样,一层石激起千层浪,教师引导学生在现有知识的基础上,各显身手,百花齐放. 水到渠成的介绍中位线概念.
2.注重参与方式的广泛性,鼓励学生合作学习
合作学习是指学生在小组或团队中进行的互助性学习. 在学习了三角形中位线的概念后,教师可出示下列问题,组织学生分组合作学习:如图1,△ABC的中位线DE与BC有什么关系?在各小组得到几种不同结果的基础上教师很自然的归纳总结出“三角形中位线定理”. 学生在合作小组中进行学习,成员之间相互交流、相互尊重,充满温情和友爱. 学生们在一起合作融洽,学习就变得更加愉快. 同时,学生在合作中学会了沟通、互助、分享,既能够尊重他人、理解他人、欣赏他人,也能使自己更好地得到他人的尊重、理解与欣赏. 并在培养学生合作与交流的同时,调动每一个学生的参与意识,课堂面貌焕然一新,使学生体验到了平等、自由和民主,同时也受到了鼓励,从而形成丰富的人生态度和体验.
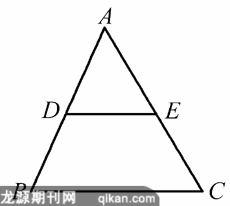
图1
3.找准设计问题的有效性,促进学生高效学习
新课程倡导的教学设计是系统的教学设计,课堂教学的有效性取决于有效的教学设计. 作为教师应带着问题进行设计. 没有问题,也就没有发现,就没有真正意义上的思考,更谈不上创新. 带着问题进行教学设计,以探索和研究的姿态,从学生的角度去思考,就会在教学设计中发现问题并找到解决问题的各种办法,就会在师生的互动中开阔视野,提高教学实效. 证明三角形中位线定理时,可以设计这三个问题:(1)“所作的平行线与中位线重合吗”;(2)“为什么会重合”;(3)“重合后能得到什么结论”这些问题产生疑问.问题的解决就使得旧知识的缺陷,得以弥补;从而培养学生发现问题、提出问题、解决问题的能力.
数学课堂要精彩,取决于教师的素质与能力、教师的经验和智慧. 我们要以有效课堂教学设计为突破口,不断推进素质教育和新课程向纵深发展,努力实现教学过程的最优化、教学效果的最大化,不断提高数学课堂的有效性.
作者简介:朱昌宝,男,1972年生,江苏通州人,本科学历,学士学位,中学一级教师,通州市“名师之路”成员. 近两年在《中学数学教学参考》、《数学教育研究》、《中学数学教与学》、《中学理科》等报刊发表论文40余篇.
下面是八年级数学第二学期三角形中位线教学中的一个教学片段:
……
师:这一节课我们一起研究三角形中位线.
师:首先我们给三角形中位线下个定义.
(边写边说:连接三角形两边中点的线段叫做三角形中位线. )
师:请同学们画出三角形的所有中位线.
(同学们迅速拿出纸和笔,认真的画起来. )
师:请问三角形共有几条中位线?
生1:三条.
生2:一条.
师:到底有几条呢?
大部分学生高声回答:3条.
师:回答得很好!三角形的中位线共有三条,并且三角形的中位线具有很重要的性质.
板书:三角形中位线定理 三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
师:下面,我们利用三角形中位线定理来解决一些题目.
……
诊断分析
作为听课教师,我们都有一种感觉:执教者开门见山,平铺直叙,直现主题,好像在追赶即将到站的班车. 对于新知识,学生犹如雾里看花,水中望月,没有了理解和摸索,缺少了反思和探究. 纵观这一教学片段,我认为至少存在以下几个方面的问题:
一、教学内容偏离了大纲要求
教材对三角形中位线的三维目标是:(1)知识与技能:使学生理解三角形中位线的概念,掌握三角形中位线定理,同时要会用三角形中位线定理进行有关的论证和计算;(2)过程与方法:培养学生动手动脑、发现问题、解决问题的能力;(3)情感、态度及价值观:对学生进行实践——认识——实践的辩证唯物主义认识论教育. 显然,在这教学过程中,学生只能被动的接受知识,没有了观察、猜测、实验. 课堂充满了教师填鸭式的灌输,没有了问题指向. 希伯特等人指出:“问题为本学习所指的,不仅是在以学科为中心的课程中加入一些问题解决活动,更是构想课程的一种方法”. 可见,本课设计不合理,无法达到“为学习设计课堂”. (加涅语)
另外,教材上在三角形中位线定理的证法中,利用了数学中的化归思想,这正是学生的薄弱环节. 根据本节课的内容和学生的实际水平,宜采用的是引导发现法和直观演示法. 在引出三角形中位线定理后,通过投影仪进行教具的直观演示,引导启发学生,让学生理解线段间的倍分问题,最终可以化归为我们很熟悉的线段相等问题.通过演示,使学生在获得感性知识的同时,为掌握理性知识创造条件.这样做,符合教学论中的直观性和可接受性原则.
二、教学导入远离了生活实际
开门见山地引如主题,本无可厚非,但就三角形中位线这一内容与我们的生活息息相关,数学教学生活化是时下较为流行的提法与做法,因此,教学设计中,可以通过解决测量河宽、建筑物高度等问题引入新课,毕竟,数学情境是联系数学与现实的纽带,是沟通数学与现实生活的桥梁. 通过实际问题让学生认识中位线定理的现实意义,加深对中位线定理的理解. 通过数学模型与生活实例挂钩,促进学生主动为解决问题而探索三角形中位线运用原理,唤醒学生参与意识,让数学知识因贴近生活而变得有趣,使学生领悟数学“源于生活、又用于生活”的道理,从而更主动地投入学习、探索之中.
三、教学过程忽视了思想生成
三角形中位线定理内容简洁,但不应淡化其生成过程. 新课标指出,课堂教学要重视知识的形成过程,包括渗透知识的文化背景、实际应用背景等,这些能大大激发学生对知识的好奇性,并积极主动地参与教学活动;让学生作出三角形的所有中位线(3条),不仅可以让学生更清楚地认识中位线,而且在不知不觉中分化了这节课的难点,并为下面找中位线与第三边的数量、位置关系作好了准备. 但是,在生2回答错误的情况下,教师一带而过,缺少了师生、生生之间的有效交流与平等对话,活生生的拔掉了学生知识网络建构的桩基. 三角形中位线生成有多种途径、多种方法,教师缺少了引领,没有重点突出某种生成过程.
四、教学方法漠视了数学实验
三角形中位线定理是初中几何的一个重要知识内容. 就事论事,只能让学生学会死搬硬套,而且只是暂时性的掌握内容,无法真正实现学数学、用数学的目的. 数学实验是指为研究或获得某种数学结论,验证某种数学猜想,实验者运用一定的方法,在特定的实验条件下所进行的一种数学探究活动,其目的是引导学生参与实践、自主探索、合作交流. 在三角形中位线定理的引入上,教师没有为学生提供和创设以数学实验为情境的数学问题,无法培养学生的数学实验技能,没有为学生猜想保驾护航,丧失了提升学生创新、创造能力的机会.
实际操作时,可以通过“回忆——作图——设疑——探索——发现——论证”而让学生掌握三角形中位线与第三边的数量关系和位置关系,并且对教材中的论证方法有了较深的印象,从而突破本节课的难点.
结合教学实情,笔者认为可以从以下几个方面进行改进:
1.重视导入方式的开放性,激发学生自主学习
恰当适时的课堂导入可激发学生的学习兴趣,产生学习动机,引起学生对所学课题的关注,传达教学意图,为学习新知识、新概念和新技能做鼓动和铺垫. 良好的开端是成功的一半. 上课伊始,教师可先提出下列问题:有一个池塘岸边设有两观测点,不能直接到达,现需要在它们之间接一电话线,请你设法测出它们之间的距离. 思维永远是从问题开始的. 教学过程是一个提出问题和解决问题的持续不断的活动,只要教师有意识地设计出悬念,就能从“悬”中激发学生的求知欲,吸引学生的注意力,学生就会产生“愿闻其详”的心情. 这样,一层石激起千层浪,教师引导学生在现有知识的基础上,各显身手,百花齐放. 水到渠成的介绍中位线概念.
2.注重参与方式的广泛性,鼓励学生合作学习
合作学习是指学生在小组或团队中进行的互助性学习. 在学习了三角形中位线的概念后,教师可出示下列问题,组织学生分组合作学习:如图1,△ABC的中位线DE与BC有什么关系?在各小组得到几种不同结果的基础上教师很自然的归纳总结出“三角形中位线定理”. 学生在合作小组中进行学习,成员之间相互交流、相互尊重,充满温情和友爱. 学生们在一起合作融洽,学习就变得更加愉快. 同时,学生在合作中学会了沟通、互助、分享,既能够尊重他人、理解他人、欣赏他人,也能使自己更好地得到他人的尊重、理解与欣赏. 并在培养学生合作与交流的同时,调动每一个学生的参与意识,课堂面貌焕然一新,使学生体验到了平等、自由和民主,同时也受到了鼓励,从而形成丰富的人生态度和体验.

图1
3.找准设计问题的有效性,促进学生高效学习
新课程倡导的教学设计是系统的教学设计,课堂教学的有效性取决于有效的教学设计. 作为教师应带着问题进行设计. 没有问题,也就没有发现,就没有真正意义上的思考,更谈不上创新. 带着问题进行教学设计,以探索和研究的姿态,从学生的角度去思考,就会在教学设计中发现问题并找到解决问题的各种办法,就会在师生的互动中开阔视野,提高教学实效. 证明三角形中位线定理时,可以设计这三个问题:(1)“所作的平行线与中位线重合吗”;(2)“为什么会重合”;(3)“重合后能得到什么结论”这些问题产生疑问.问题的解决就使得旧知识的缺陷,得以弥补;从而培养学生发现问题、提出问题、解决问题的能力.
数学课堂要精彩,取决于教师的素质与能力、教师的经验和智慧. 我们要以有效课堂教学设计为突破口,不断推进素质教育和新课程向纵深发展,努力实现教学过程的最优化、教学效果的最大化,不断提高数学课堂的有效性.
作者简介:朱昌宝,男,1972年生,江苏通州人,本科学历,学士学位,中学一级教师,通州市“名师之路”成员. 近两年在《中学数学教学参考》、《数学教育研究》、《中学数学教与学》、《中学理科》等报刊发表论文40余篇.

