速度关联类问题求解
孙尔林

在高中运动的合成与分解学习中,学生常对该如何分解速度搞不清楚或很难理解,其主要原因是无法弄清楚哪一个是合速度、哪一个是分速度.这里有一个简单的方法:物体的实际运动方向就是合速度的方向,然后分析这个合速度所产生的实际效果,以确定两个分速度的方向.
一、绳、杆连接的物体
绳、杆等连接的物体,在运动过程中,其两端物体的速度通常是不一样的,但两端物体的速度是有联系的,称为“关联”速度.关联速度的关系——物体沿杆(或绳)方向的速度分量大小相等,因此,求这类问题时,首先要明确绳连物体的速度为合速度,然后将两物体的速度分别分解成沿绳方向和与绳垂直方向,令两物体沿绳方向的速度相等即可求出.
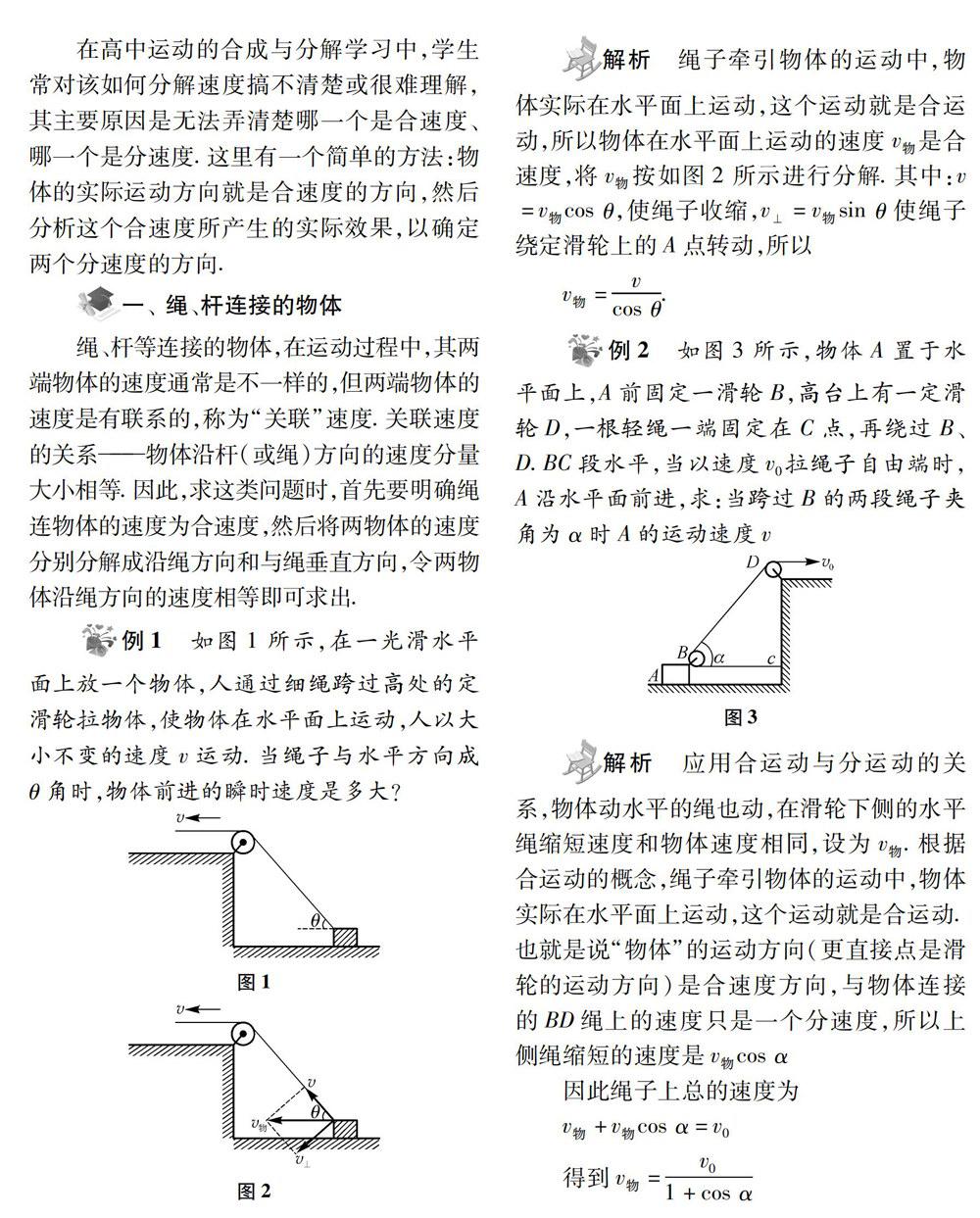
例1 如图1所示,在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?
解析 绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,所以物体在水平面上运动的速度”物是合速度,将v物 按如图2所示进行分解.其中:v= v物 cosθ,使绳子收缩,vI=v物 sinθ使绳子绕定滑轮上的A点转动,所以
v物=v/cosθ.
例2 如圖3所示,物体A置于水平面上,A前固定一滑轮B,高台上有一定滑轮D,一根轻绳一端固定在C点,再绕过B、D.BC段水平,当以速度v0 拉绳子自由端时,A沿水平面前进,求:当跨过B的两段绳子夹角为α时A的运动速度v
解析 应用合运动与分运动的关系,物体动水平的绳也动,在滑轮下侧的水平绳缩短速度和物体速度相同,设为 v物.根据合运动的概念,绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动.也就是说“物体”的运动方向(更直接点是滑轮的运动方向)是合速度方向,与物体连接的BD绳上的速度只是一个分速度,所以上侧绳缩短的速度是v物 cosα
因此绳子上总的速度为
v物十v物 cosα=v0
得到v物=v0/1+cosα
例3 一根长为L的杆OA,O端用铰链固定,另一端固定着一个小球A,靠在一个质量为M,高为h的物块上,如图4所示,物块以速度v向右运动,试求当杆与水平方向夹角为θ时,求小球4的线速度vA.
解析 选取物与棒接触点B为连结点,B点的实际速度(合速度)也就是物块速度v;B点又在棒上,参与沿棒向A点滑动的速度v1和绕O点转动的线速度v2,因此,将这个合速度沿棒及垂直于棒的两个方向分解.
二、相互接触的物体
求相互接触物体的速度关联问题时,首先要明确两接触物体的速度,分析弹力的方向,然后将两物体的速度分别沿弹力的方向和垂直于弹力的方向进行分解,令两物体沿弹力方向的速度相等即可求出.
例4 一个半径为R的半圆柱沿水平方向向右以速度v0匀速运动.在半圆柱上放置一根竖直杆,此杆只能沿竖直方向运动,如图6所示.当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ时,求竖直杆运动的速度.
解析 设竖直杆运动的速度为v1方向竖直向上,由于弹力沿OP方向,所以有v0、vl在OP方向的投影相等,即有
v0 sin θ=v1 cosθ
解得v1= v0 tan θ
运动物体间速度关联关系,往往是有些高考命题的切人点.而寻找这种关系则是普遍感觉的难点速度关联问题,关键是找到关联点,即双方所服从的共同的制约条件,即等量关系.找关联点应当从两个研究对象的共同之处着眼.速度的分解的理论是解该类题常用到的.切记,可以分解的一定是实际速度,即实际速度是合速度.


在高中运动的合成与分解学习中,学生常对该如何分解速度搞不清楚或很难理解,其主要原因是无法弄清楚哪一个是合速度、哪一个是分速度.这里有一个简单的方法:物体的实际运动方向就是合速度的方向,然后分析这个合速度所产生的实际效果,以确定两个分速度的方向.
一、绳、杆连接的物体
绳、杆等连接的物体,在运动过程中,其两端物体的速度通常是不一样的,但两端物体的速度是有联系的,称为“关联”速度.关联速度的关系——物体沿杆(或绳)方向的速度分量大小相等,因此,求这类问题时,首先要明确绳连物体的速度为合速度,然后将两物体的速度分别分解成沿绳方向和与绳垂直方向,令两物体沿绳方向的速度相等即可求出.
例1 如图1所示,在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?
解析 绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,所以物体在水平面上运动的速度”物是合速度,将v物 按如图2所示进行分解.其中:v= v物 cosθ,使绳子收缩,vI=v物 sinθ使绳子绕定滑轮上的A点转动,所以
v物=v/cosθ.
例2 如圖3所示,物体A置于水平面上,A前固定一滑轮B,高台上有一定滑轮D,一根轻绳一端固定在C点,再绕过B、D.BC段水平,当以速度v0 拉绳子自由端时,A沿水平面前进,求:当跨过B的两段绳子夹角为α时A的运动速度v
解析 应用合运动与分运动的关系,物体动水平的绳也动,在滑轮下侧的水平绳缩短速度和物体速度相同,设为 v物.根据合运动的概念,绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动.也就是说“物体”的运动方向(更直接点是滑轮的运动方向)是合速度方向,与物体连接的BD绳上的速度只是一个分速度,所以上侧绳缩短的速度是v物 cosα
因此绳子上总的速度为
v物十v物 cosα=v0
得到v物=v0/1+cosα
例3 一根长为L的杆OA,O端用铰链固定,另一端固定着一个小球A,靠在一个质量为M,高为h的物块上,如图4所示,物块以速度v向右运动,试求当杆与水平方向夹角为θ时,求小球4的线速度vA.
解析 选取物与棒接触点B为连结点,B点的实际速度(合速度)也就是物块速度v;B点又在棒上,参与沿棒向A点滑动的速度v1和绕O点转动的线速度v2,因此,将这个合速度沿棒及垂直于棒的两个方向分解.
二、相互接触的物体
求相互接触物体的速度关联问题时,首先要明确两接触物体的速度,分析弹力的方向,然后将两物体的速度分别沿弹力的方向和垂直于弹力的方向进行分解,令两物体沿弹力方向的速度相等即可求出.
例4 一个半径为R的半圆柱沿水平方向向右以速度v0匀速运动.在半圆柱上放置一根竖直杆,此杆只能沿竖直方向运动,如图6所示.当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ时,求竖直杆运动的速度.
解析 设竖直杆运动的速度为v1方向竖直向上,由于弹力沿OP方向,所以有v0、vl在OP方向的投影相等,即有
v0 sin θ=v1 cosθ
解得v1= v0 tan θ
运动物体间速度关联关系,往往是有些高考命题的切人点.而寻找这种关系则是普遍感觉的难点速度关联问题,关键是找到关联点,即双方所服从的共同的制约条件,即等量关系.找关联点应当从两个研究对象的共同之处着眼.速度的分解的理论是解该类题常用到的.切记,可以分解的一定是实际速度,即实际速度是合速度.

