试论几何推理的若干特点
周 超
说到推理,人们首先想到的是几何推理;而说起几何推理,往往又是指演绎推理. 实际上,“推理”一词有着广泛的意义,目前,一个普遍的看法是:任何与解决困难有关的动作、尝试与错误、程序都常被作为一种推理的形式,特别地,任何从已有信息中提取新信息的过程都被看作是推理. 按照这种观点,几何推理显然不等于演绎推理. 由于几何的多样性,几何推理的形式和水平也非常丰富,其中除了演绎推理外,还包括视觉推理,自然推理,归纳推理,类比推理等.
此外还需要更新的一个观念是:演绎推理也不等于传统的三段论. 这里有两个原因,一是作为演绎推理基础的逻辑已经从狭窄的形式逻辑中解放出来,出现了各种各样的逻辑;二是三段论只不过是形式逻辑中的一种推理方式,除此之外,还有关系推理.
随着几何推理的外延的拓展,我们认为,它具有以下三个方面的特点:
1 几何推理往往借助于直观
心理学的研究表明,几何活动一般涉及三种认知过程(Mammana and Villani, 1998):
确认二维和三维空间中的图形和形状,
这种确认依赖于一些特殊的规则,
这些规则与构造和表征的方式相对是独立的.
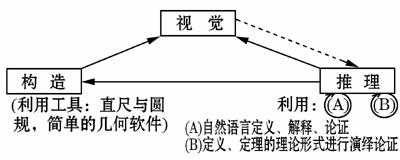
图1 认知活动的三个过程
下面我们通过一个简单的例子来分析具体几何活动(解决几何问题)中的上述三种认知过程.
例1 证明平行四边形对角线互相平分.
视觉过程 几何中的视觉过程涉及三个方面的变化:维度的变化,图形的变化和观察点(或者说背景)的变化. 其中,维度变化是观察一个图形所表示对象的基本的认知过程,在问题解决中担负着启发探索的角色. 图形变化,或者操作性理解,则相对来说比较复杂,并且不容易意识到. 而背景的变化则相对来说比较熟悉.
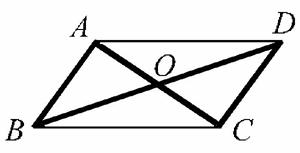
图2
在处理平面几何问题时,视觉过程通常是从二维角度来理解图形. 例如,在本题中(图2),视觉过程把平行四边形看作一个表面,如桌子的表面,或者在其他平面(而不是正面)上的正方形,或者平行四边形. 当图形是通过工具(直尺和圆规,或者计算机软件)构造出来时,更容易被看作是一种几何表示而不是实际物体. 对于本题来说,解题的关键是“看出”图中有一对全等的三角形(图中的粗线部分). 因此,视觉过程的主要作用是感知图形的整体形态,并将图形从背景中分离出来.
构造过程 几何构造过程的一个重要的特征是维度或者位置上的变化. 例如,在图2中,“平行四边形”被看作是几个一维或者二维图形:“线段”、“顶点”、“角”在平面上的组合;而粗线三角形△OAB则可以看作是由平行四边形的一条边AB、角OAB和角AOB构成的,由此使我们可以分别讨论△OAB和△OCD的边角之间的关系,并进而推出两个三角形全等. 因此,几何构筑过程的作用主要是把一个图形分解为基本成分或者组合成一些基本图形,然后,利用基本成分或者基本图形的关系来解决相应的几何问题.
推理过程 推理过程涉及对知识的扩展、证明和解释,并且要借助于已有知识和逻辑规则. 在本题中,图形首先是作为数学对象:“平行四边形”,而不仅仅是一种形状或者一个构造,由此得到的是对可能的几何结构和线段之间的关系(对象的性质)的理解,这种结构和关系并且通过记号得到强调. 例如,由“平行四边形”的定义推出AB=CD,∠OAB=∠OCD,∠AOB=∠COD,从而推得△OAB和△OCD全等,并最终完成证明过程.
从上述例子可以看到,在具体的几何活动中,这三种认知过程往往是纠缠在一起的. 其中,视觉过程和构造过程这两个直观的过程往往有助于推理过程的形成. 当然,这里的直观并非只是图形的直观,也包括符号及其它抽象形式的直观. 例如,在上面的例子中,由△OAB∽△OCD,可依据字母的排列顺序“直观地”推出:OA=OC,OB=OD,即平行四边形的对角线互相平分.
2 几何推理具有明显的层次性
早在上世纪50年代,荷兰的范希尔夫妇就把几何思考水平划分为如下五个层次(Burger and Shaughnessy,1986):
层次0 视觉 (visuality)
儿童能通过整体轮廓辨认图形,并能操作其几何构图元素(如边、角);能画图或仿画图形,使用标准或不标准名称描述几何图形;能根据对形状的操作解决几何问题,但无法使用图形之特征或要素名称分析图形,也无法对图形做概括的论述. 例如:儿童可能会说某个图形是三角形,因为它看起来象一个三明治.
层次1 分析(analysis)
儿童能分析图形的组成要素及特征,并依此建立图形的特性,利用这些特性解决几何问题,但无法解释性质间的关系,也无法了解图形的定义;能根据组成要素比较两个形体,利用某一性质做图形分类,但无法解释图形某些性质之间的关联,也无法导出公式和使用正式的定义. 例如:儿童会知道三角形有三条边和三个角,但不能理解如果内角愈大,则对边愈长的性质.
层次2 非形式化的演绎 (informal deduction)
儿童能建立图形及图形性质之间的关系,可以提出非形式化的推论,了解建构图形的要素,能进一步探求图形的内在属性和其包含关系,使用公式与定义及发现的性质做演绎推论. 但不能了解证明与定理的重要性,不能由不熟悉的前提去建立证明结果的成立,也未能建立定理网络之间的内在关系. 例如:学生了解了等腰三角形的性质后,他们会推出等腰直角三角形同时也是直角三角形的一种,因为等腰直角三角形较直角三角形多了一些性质的限制. 因此,学童能作一些非正式的说明但还不能作系统性的证明.
层次3 形式的演绎 (formal deduction)
学生可以了解到证明的重要性和了解“不定义元素”、“定理”和“公理”的意义,确信几何定理是需要形式逻辑推演才能建立的,理解解决几何问题必须具备充分或必要条件;能猜测并尝试用演绎方式证实其猜测,能够以逻辑推理解释几何学中的公理、定义、定理等,也能推理出新的定理,建立定理间的关系网络,能比较一个定理的不同证明方式;能理解证明中的必要与充分条件,例如至少有一条边对应相等或至少一个角对应相等是证明两个三角形全等的必要条件,两角夹边对应相等则是两三角形全等的充分条件;能写出一定理的逆定理,如平行四边形的对角线互相平分,其逆定理是对角线互相平分的四边形是平行四边形.
层次4 严密性(rigior )
在这个层次,能在不同的公理系统下严谨地建立定理,以分析、比较不同的几何系统,如欧氏几何与非欧氏几何系统的比较.
范希尔夫妇的上述五个几何思考层次得到了许多后继研究的证实,并被广为应用. 而实际上,这五个思考层次也可以看作是几何推理的五个层次. 这种层次的划分,对几何课程的制定及学生的学习都有着重要的实际意义.
3 几何推理方式的多样性
正是由于几何推理往往涉及多种过程并且可以划分为多种层次,因此,其表现形式也具有多样性,大体上可以区分出三种基本形式:
(1)图形推理
这是一种依赖于视觉过程和构造过程的直观描述. 例如,通常我们说的几何“无字证明”就属于这种情况. 我们来看下面的问题:
例2 在下面的图形中,AC是矩形ABCD的对角线,当U点在对角线AC上移动时,比较阴影部分的面积的大小.
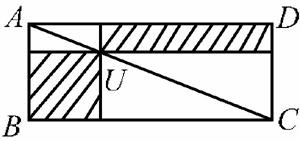
“无字证明”:
①

②


③

(2)自然推理
一种用普通语言进行描述、解释和论证的即时的表现. 自然推理往往伴随着图形推理,而大多数情况下,它是对图形推理的一种口语化的描述. 目前我国新的数学课程标准中,在初中低年级推行的所谓几何“说明”实际上就属于自然推理.
(3)理论推理
也即演绎法,与逻辑有密切的联系,其表现形式可以是纯粹的符号,也可以是自然语言,但这两种形式对学生来说无论是难度上还是意义上都是不同的.
在几何中,用于证明的演绎推理需要两个条件:
■命题的利用,而每一个命题又以特殊的理论体系为前提:公理、定义、定理、假设、猜想等;
■推理的每一步都依赖于定理、公理或者定义.
换句话说,这里所提供的信息的形式是不同的:它只能是命题;而信息的组织也是不同的,通常有三个水平:一是整体水平,其中的每一步都与结论有关;二是局部水平,涉及题设、定义和定理、结论之间的组织;三是微观水平,作为工具的命题的内部组织,包括两部分:条件与结论. 显然,在局部水平的组织上,自然推理过程和理论推理过程有本质的差异,也就是说,理论推理不同于我们日常生活中用到的推理方式.
近年来,随着“几何推理”的外延的扩展,它也从单纯的证明工具转变成为发现各种几何事实和关系的途径,成为知识的扩展和解释的推进器,成为一种说服别人相信几何猜想的手段. 正如汉德森(D. Henderson)所说(Mammana and Villani, 1998):
■生动的几何推理更多地注意隐藏在公式和符号后面的意义——一种以直觉、想象和现实经验为基础的意义;
■生动的几何推理知道几何中的定义、假设是随着背景和观点的改变而改变的;
■生动的几何推理是作猜想、寻找反例、发展联系;
■生动的几何推理总是问:为什么?
参考文献
[1] Burger, W. and Shaughnessy, W. (1986) "Characterizing the van Hiele Levels of Development in Geometry." Journal for Research in Mathematics Education 17: 31-48.
[2] Mammana, C. and Villani, V.(1998). Perspectives on the Teaching of Geometry for the 21st Century.(New ICMI Study Series Volume 5) Dordrecht: Kluwer.
作者简介:周超,女,1978年8月出生,江苏高邮人,主要研究方向为数学教育理论与实践.
说到推理,人们首先想到的是几何推理;而说起几何推理,往往又是指演绎推理. 实际上,“推理”一词有着广泛的意义,目前,一个普遍的看法是:任何与解决困难有关的动作、尝试与错误、程序都常被作为一种推理的形式,特别地,任何从已有信息中提取新信息的过程都被看作是推理. 按照这种观点,几何推理显然不等于演绎推理. 由于几何的多样性,几何推理的形式和水平也非常丰富,其中除了演绎推理外,还包括视觉推理,自然推理,归纳推理,类比推理等.
此外还需要更新的一个观念是:演绎推理也不等于传统的三段论. 这里有两个原因,一是作为演绎推理基础的逻辑已经从狭窄的形式逻辑中解放出来,出现了各种各样的逻辑;二是三段论只不过是形式逻辑中的一种推理方式,除此之外,还有关系推理.
随着几何推理的外延的拓展,我们认为,它具有以下三个方面的特点:
1 几何推理往往借助于直观
心理学的研究表明,几何活动一般涉及三种认知过程(Mammana and Villani, 1998):
确认二维和三维空间中的图形和形状,
这种确认依赖于一些特殊的规则,
这些规则与构造和表征的方式相对是独立的.

图1 认知活动的三个过程
下面我们通过一个简单的例子来分析具体几何活动(解决几何问题)中的上述三种认知过程.
例1 证明平行四边形对角线互相平分.
视觉过程 几何中的视觉过程涉及三个方面的变化:维度的变化,图形的变化和观察点(或者说背景)的变化. 其中,维度变化是观察一个图形所表示对象的基本的认知过程,在问题解决中担负着启发探索的角色. 图形变化,或者操作性理解,则相对来说比较复杂,并且不容易意识到. 而背景的变化则相对来说比较熟悉.

图2
在处理平面几何问题时,视觉过程通常是从二维角度来理解图形. 例如,在本题中(图2),视觉过程把平行四边形看作一个表面,如桌子的表面,或者在其他平面(而不是正面)上的正方形,或者平行四边形. 当图形是通过工具(直尺和圆规,或者计算机软件)构造出来时,更容易被看作是一种几何表示而不是实际物体. 对于本题来说,解题的关键是“看出”图中有一对全等的三角形(图中的粗线部分). 因此,视觉过程的主要作用是感知图形的整体形态,并将图形从背景中分离出来.
构造过程 几何构造过程的一个重要的特征是维度或者位置上的变化. 例如,在图2中,“平行四边形”被看作是几个一维或者二维图形:“线段”、“顶点”、“角”在平面上的组合;而粗线三角形△OAB则可以看作是由平行四边形的一条边AB、角OAB和角AOB构成的,由此使我们可以分别讨论△OAB和△OCD的边角之间的关系,并进而推出两个三角形全等. 因此,几何构筑过程的作用主要是把一个图形分解为基本成分或者组合成一些基本图形,然后,利用基本成分或者基本图形的关系来解决相应的几何问题.
推理过程 推理过程涉及对知识的扩展、证明和解释,并且要借助于已有知识和逻辑规则. 在本题中,图形首先是作为数学对象:“平行四边形”,而不仅仅是一种形状或者一个构造,由此得到的是对可能的几何结构和线段之间的关系(对象的性质)的理解,这种结构和关系并且通过记号得到强调. 例如,由“平行四边形”的定义推出AB=CD,∠OAB=∠OCD,∠AOB=∠COD,从而推得△OAB和△OCD全等,并最终完成证明过程.
从上述例子可以看到,在具体的几何活动中,这三种认知过程往往是纠缠在一起的. 其中,视觉过程和构造过程这两个直观的过程往往有助于推理过程的形成. 当然,这里的直观并非只是图形的直观,也包括符号及其它抽象形式的直观. 例如,在上面的例子中,由△OAB∽△OCD,可依据字母的排列顺序“直观地”推出:OA=OC,OB=OD,即平行四边形的对角线互相平分.
2 几何推理具有明显的层次性
早在上世纪50年代,荷兰的范希尔夫妇就把几何思考水平划分为如下五个层次(Burger and Shaughnessy,1986):
层次0 视觉 (visuality)
儿童能通过整体轮廓辨认图形,并能操作其几何构图元素(如边、角);能画图或仿画图形,使用标准或不标准名称描述几何图形;能根据对形状的操作解决几何问题,但无法使用图形之特征或要素名称分析图形,也无法对图形做概括的论述. 例如:儿童可能会说某个图形是三角形,因为它看起来象一个三明治.
层次1 分析(analysis)
儿童能分析图形的组成要素及特征,并依此建立图形的特性,利用这些特性解决几何问题,但无法解释性质间的关系,也无法了解图形的定义;能根据组成要素比较两个形体,利用某一性质做图形分类,但无法解释图形某些性质之间的关联,也无法导出公式和使用正式的定义. 例如:儿童会知道三角形有三条边和三个角,但不能理解如果内角愈大,则对边愈长的性质.
层次2 非形式化的演绎 (informal deduction)
儿童能建立图形及图形性质之间的关系,可以提出非形式化的推论,了解建构图形的要素,能进一步探求图形的内在属性和其包含关系,使用公式与定义及发现的性质做演绎推论. 但不能了解证明与定理的重要性,不能由不熟悉的前提去建立证明结果的成立,也未能建立定理网络之间的内在关系. 例如:学生了解了等腰三角形的性质后,他们会推出等腰直角三角形同时也是直角三角形的一种,因为等腰直角三角形较直角三角形多了一些性质的限制. 因此,学童能作一些非正式的说明但还不能作系统性的证明.
层次3 形式的演绎 (formal deduction)
学生可以了解到证明的重要性和了解“不定义元素”、“定理”和“公理”的意义,确信几何定理是需要形式逻辑推演才能建立的,理解解决几何问题必须具备充分或必要条件;能猜测并尝试用演绎方式证实其猜测,能够以逻辑推理解释几何学中的公理、定义、定理等,也能推理出新的定理,建立定理间的关系网络,能比较一个定理的不同证明方式;能理解证明中的必要与充分条件,例如至少有一条边对应相等或至少一个角对应相等是证明两个三角形全等的必要条件,两角夹边对应相等则是两三角形全等的充分条件;能写出一定理的逆定理,如平行四边形的对角线互相平分,其逆定理是对角线互相平分的四边形是平行四边形.
层次4 严密性(rigior )
在这个层次,能在不同的公理系统下严谨地建立定理,以分析、比较不同的几何系统,如欧氏几何与非欧氏几何系统的比较.
范希尔夫妇的上述五个几何思考层次得到了许多后继研究的证实,并被广为应用. 而实际上,这五个思考层次也可以看作是几何推理的五个层次. 这种层次的划分,对几何课程的制定及学生的学习都有着重要的实际意义.
3 几何推理方式的多样性
正是由于几何推理往往涉及多种过程并且可以划分为多种层次,因此,其表现形式也具有多样性,大体上可以区分出三种基本形式:
(1)图形推理
这是一种依赖于视觉过程和构造过程的直观描述. 例如,通常我们说的几何“无字证明”就属于这种情况. 我们来看下面的问题:
例2 在下面的图形中,AC是矩形ABCD的对角线,当U点在对角线AC上移动时,比较阴影部分的面积的大小.

“无字证明”:
①

②


③

(2)自然推理
一种用普通语言进行描述、解释和论证的即时的表现. 自然推理往往伴随着图形推理,而大多数情况下,它是对图形推理的一种口语化的描述. 目前我国新的数学课程标准中,在初中低年级推行的所谓几何“说明”实际上就属于自然推理.
(3)理论推理
也即演绎法,与逻辑有密切的联系,其表现形式可以是纯粹的符号,也可以是自然语言,但这两种形式对学生来说无论是难度上还是意义上都是不同的.
在几何中,用于证明的演绎推理需要两个条件:
■命题的利用,而每一个命题又以特殊的理论体系为前提:公理、定义、定理、假设、猜想等;
■推理的每一步都依赖于定理、公理或者定义.
换句话说,这里所提供的信息的形式是不同的:它只能是命题;而信息的组织也是不同的,通常有三个水平:一是整体水平,其中的每一步都与结论有关;二是局部水平,涉及题设、定义和定理、结论之间的组织;三是微观水平,作为工具的命题的内部组织,包括两部分:条件与结论. 显然,在局部水平的组织上,自然推理过程和理论推理过程有本质的差异,也就是说,理论推理不同于我们日常生活中用到的推理方式.
近年来,随着“几何推理”的外延的扩展,它也从单纯的证明工具转变成为发现各种几何事实和关系的途径,成为知识的扩展和解释的推进器,成为一种说服别人相信几何猜想的手段. 正如汉德森(D. Henderson)所说(Mammana and Villani, 1998):
■生动的几何推理更多地注意隐藏在公式和符号后面的意义——一种以直觉、想象和现实经验为基础的意义;
■生动的几何推理知道几何中的定义、假设是随着背景和观点的改变而改变的;
■生动的几何推理是作猜想、寻找反例、发展联系;
■生动的几何推理总是问:为什么?
参考文献
[1] Burger, W. and Shaughnessy, W. (1986) "Characterizing the van Hiele Levels of Development in Geometry." Journal for Research in Mathematics Education 17: 31-48.
[2] Mammana, C. and Villani, V.(1998). Perspectives on the Teaching of Geometry for the 21st Century.(New ICMI Study Series Volume 5) Dordrecht: Kluwer.
作者简介:周超,女,1978年8月出生,江苏高邮人,主要研究方向为数学教育理论与实践.

