解析动力学多过程问题
郑行军


多过程问题是指如果物体的运动涉及多个阶段,就是多个模型在时间和空间上有机地组合在一起,这类问题统称为多过程问题.
处理多过程问题时,受力分析和运动情况分析是解题的关键,特别是对运动过程较复杂的问题.分析时,一定要弄清楚整个过程中物体的加速度是否相同,若不同,必须分阶段处理,加速度改变时的速度是前后过程联系的桥梁,是多过程问题中的必求量,在分析处理时要遵循先求该时刻的速度,再求其他物理量.分析受力时,要注意前后过程中哪些力发生了变化,哪些力没发生变化.
多过程问题解题策略有:
1.思维方法呈现
1.1 程序法:程序法就是按时间的先后顺序对题目给出的物体运动过程(或不同的状态)进行分析计算的解题方法.分析这类问题时,首先正确划分题目中有几种不同的过程或状态,然后对每个过程或状态进行具体分析,列方程求解,最后综合各个过程,得出最终的结果.
1.2 分析法:分析法是将未知推演还原为已知的思维方法,用分析法研究问题时,需要从题意要求的待求量出发,然后按一定的逻辑思维顺序逐步分析、推演,直到待求量完全可以用已知量表达为止.
2.解题方法归类
2.1 公式法:对物体不同的运动阶段进行分析,选择合适的动力学公式进行求解,采用公式法关键在于求解两个阶段连接点的速度.
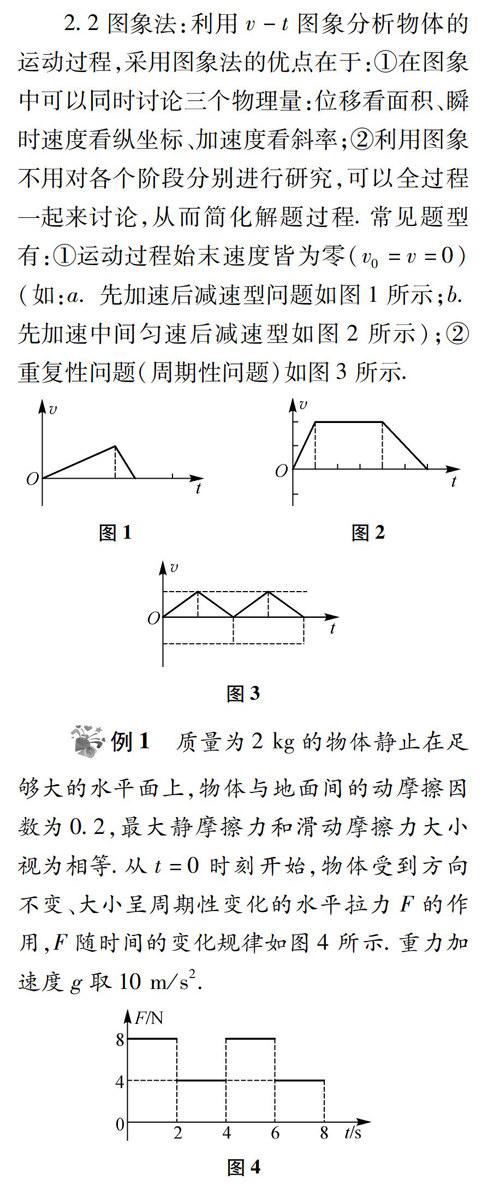
2.2 图象法:利用v-t图象分析物体的运动过程,采用图象法的优点在于:①在图象中可以同时讨论三个物理量:位移看面积、瞬时速度看纵坐标、加速度看斜率;②利用图象不用对各个阶段分别进行研究,可以全过程一起来讨论,从而简化解题过程.常见题型有:①运动过程始末速度皆为零(v0=v=0)(如:a.先加速后减速型问题如图l所示;b.先加速中间匀速后减速型如图2所示);②重复性问题(周期性问题)如图3所示.
例1 质量为2 kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间的变化规律如图4所示.重力加速度g取10 m/s2.
(1)分别计算2s末、4s末、6s末物体的速度大小:
(2)画出物体在0~6 s内的v-t图线.
(3)求物体在0~6 s内的位移.
解析 (1)在0~2 s内,由牛顿第二定律得F1-μmg=ma1,解得a1=2m/s2,所以2s末物体的速度大小为v1=a1t1=4m/s;物体在2~4 s内,F2 =μmg,做匀速直线运动,4s末的速度大小为v2=v1=4 m/s;在4~6 s内,物体的加速度大小a3=a1=2 m/s2,所以,物体6s末的速度大小为v3=v2 +a3t3 =8m/s
(2)在0~2 s内,物体做初速度为零的匀加速直线運动,对应的v-t图象是一条经过原点的倾斜线段;在2~4 s内,物体做匀速直线运动,对应的v-t图象是一条平行于时间轴的水平线段;在4~6 s内,物体做匀加速直线运动,对应的v-t图象是一条倾斜线段.画出的v-t图象如图5所示
(3)根据v-t图象,物体在0~6 s内的位移为图象与t轴围成的面积,求面积可得:
s=1/2×2×4 +2×4+1/2×2×(4+8) =24 m
综上所述,多过程问题实际是多种运动规律的组合,在分析的过程中涉及运动和力的问题或要求分析物体的动力学特点,要用动力学方法求解.在建立两运动之间的联系时,要把转折点的速度作为分析重点.
例2 如图6所示,一足够长的、倾角α= 37°的斜面,固定在水平地面上.一质量m =1 kg的物体(视为质点)在水平恒定推力F作用下,从斜面底端由静止沿斜面向上运动,运动一段距离后立即撤去推力F,此后物体继续运动.在物体上升的阶段,每隔0.2 m通过速度传感器测得物体的瞬时速度的大小,下表给出了部分测量数据.物体与斜面间的动摩擦因数μ处处相同,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)物体与斜面间的动摩擦因数μ;
(2)推力F的大小;
(3)当物体向上运动到x=0.8 m时物体的瞬时速度大小.
例3 许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零).某次服务员用单手托托盘方式(如图7)给12 m远处的顾客上菜,要求全程托盘水平.托盘和手、碗之间的动摩擦因数分别为0.2、0. 15,服务员上菜最大速度为3 m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.求
(1)服务员运动的最大加速度;
(2)服务员上菜所用的最短时间;
解析 (1)设碗的质量为m,托盘的质量为M,以最大加速度运动时,碗、托盘、手保持相对静止,如图8所示.取碗为研究对象,由牛顿第二定律得:f1= ma1,碗与托盘间相对静止,则f1≤f1max=μ1 mg
解得:aI≤μ1g=0.15×10=1.5(m/s2)
取碗和托盘整体,由牛顿第二定律得:
f2=(M+m)a2
手和托盘间相对静止,则:f2≤f2max=μ2(M+m)g,解得:a2≤μ2 g=0.2×10=2( m/s2),则最大加速度:a max=1.5 m/s2
(2)服务员以最大加速度达到最大速度,然后匀速运动,再以最大加速度减速运动,所需时间最短,加速运动时间:
例4如图10所示,某滑冰运动员参加直线滑行练习,在滑行时,左右脚交替向后蹬冰,每次蹬冰的时间t1=1 s,冰面给人水平向前的动力F=165 N,左右脚交替时有t2=0.5 s的时间不用蹬冰.已知整个过程中运动员受到的阻力f=55 N,运动员总质量m=55 kg,设运动员由静止开始滑行,求开始3s内运动员的位移.



多过程问题是指如果物体的运动涉及多个阶段,就是多个模型在时间和空间上有机地组合在一起,这类问题统称为多过程问题.
处理多过程问题时,受力分析和运动情况分析是解题的关键,特别是对运动过程较复杂的问题.分析时,一定要弄清楚整个过程中物体的加速度是否相同,若不同,必须分阶段处理,加速度改变时的速度是前后过程联系的桥梁,是多过程问题中的必求量,在分析处理时要遵循先求该时刻的速度,再求其他物理量.分析受力时,要注意前后过程中哪些力发生了变化,哪些力没发生变化.
多过程问题解题策略有:
1.思维方法呈现
1.1 程序法:程序法就是按时间的先后顺序对题目给出的物体运动过程(或不同的状态)进行分析计算的解题方法.分析这类问题时,首先正确划分题目中有几种不同的过程或状态,然后对每个过程或状态进行具体分析,列方程求解,最后综合各个过程,得出最终的结果.
1.2 分析法:分析法是将未知推演还原为已知的思维方法,用分析法研究问题时,需要从题意要求的待求量出发,然后按一定的逻辑思维顺序逐步分析、推演,直到待求量完全可以用已知量表达为止.
2.解题方法归类
2.1 公式法:对物体不同的运动阶段进行分析,选择合适的动力学公式进行求解,采用公式法关键在于求解两个阶段连接点的速度.
2.2 图象法:利用v-t图象分析物体的运动过程,采用图象法的优点在于:①在图象中可以同时讨论三个物理量:位移看面积、瞬时速度看纵坐标、加速度看斜率;②利用图象不用对各个阶段分别进行研究,可以全过程一起来讨论,从而简化解题过程.常见题型有:①运动过程始末速度皆为零(v0=v=0)(如:a.先加速后减速型问题如图l所示;b.先加速中间匀速后减速型如图2所示);②重复性问题(周期性问题)如图3所示.
例1 质量为2 kg的物体静止在足够大的水平面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力和滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间的变化规律如图4所示.重力加速度g取10 m/s2.
(1)分别计算2s末、4s末、6s末物体的速度大小:
(2)画出物体在0~6 s内的v-t图线.
(3)求物体在0~6 s内的位移.
解析 (1)在0~2 s内,由牛顿第二定律得F1-μmg=ma1,解得a1=2m/s2,所以2s末物体的速度大小为v1=a1t1=4m/s;物体在2~4 s内,F2 =μmg,做匀速直线运动,4s末的速度大小为v2=v1=4 m/s;在4~6 s内,物体的加速度大小a3=a1=2 m/s2,所以,物体6s末的速度大小为v3=v2 +a3t3 =8m/s
(2)在0~2 s内,物体做初速度为零的匀加速直线運动,对应的v-t图象是一条经过原点的倾斜线段;在2~4 s内,物体做匀速直线运动,对应的v-t图象是一条平行于时间轴的水平线段;在4~6 s内,物体做匀加速直线运动,对应的v-t图象是一条倾斜线段.画出的v-t图象如图5所示
(3)根据v-t图象,物体在0~6 s内的位移为图象与t轴围成的面积,求面积可得:
s=1/2×2×4 +2×4+1/2×2×(4+8) =24 m
综上所述,多过程问题实际是多种运动规律的组合,在分析的过程中涉及运动和力的问题或要求分析物体的动力学特点,要用动力学方法求解.在建立两运动之间的联系时,要把转折点的速度作为分析重点.
例2 如图6所示,一足够长的、倾角α= 37°的斜面,固定在水平地面上.一质量m =1 kg的物体(视为质点)在水平恒定推力F作用下,从斜面底端由静止沿斜面向上运动,运动一段距离后立即撤去推力F,此后物体继续运动.在物体上升的阶段,每隔0.2 m通过速度传感器测得物体的瞬时速度的大小,下表给出了部分测量数据.物体与斜面间的动摩擦因数μ处处相同,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)物体与斜面间的动摩擦因数μ;
(2)推力F的大小;
(3)当物体向上运动到x=0.8 m时物体的瞬时速度大小.
例3 许多餐厅生意火爆,常常人满为患,为能服务更多的顾客,服务员需要用最短的时间将菜肴送至顾客处(设菜品送到顾客处速度恰好为零).某次服务员用单手托托盘方式(如图7)给12 m远处的顾客上菜,要求全程托盘水平.托盘和手、碗之间的动摩擦因数分别为0.2、0. 15,服务员上菜最大速度为3 m/s.假设服务员加速、减速运动过程中是匀变速直线运动,且可认为最大静摩擦力等于滑动摩擦力.求
(1)服务员运动的最大加速度;
(2)服务员上菜所用的最短时间;
解析 (1)设碗的质量为m,托盘的质量为M,以最大加速度运动时,碗、托盘、手保持相对静止,如图8所示.取碗为研究对象,由牛顿第二定律得:f1= ma1,碗与托盘间相对静止,则f1≤f1max=μ1 mg
解得:aI≤μ1g=0.15×10=1.5(m/s2)
取碗和托盘整体,由牛顿第二定律得:
f2=(M+m)a2
手和托盘间相对静止,则:f2≤f2max=μ2(M+m)g,解得:a2≤μ2 g=0.2×10=2( m/s2),则最大加速度:a max=1.5 m/s2
(2)服务员以最大加速度达到最大速度,然后匀速运动,再以最大加速度减速运动,所需时间最短,加速运动时间:
例4如图10所示,某滑冰运动员参加直线滑行练习,在滑行时,左右脚交替向后蹬冰,每次蹬冰的时间t1=1 s,冰面给人水平向前的动力F=165 N,左右脚交替时有t2=0.5 s的时间不用蹬冰.已知整个过程中运动员受到的阻力f=55 N,运动员总质量m=55 kg,设运动员由静止开始滑行,求开始3s内运动员的位移.

