动态平衡问题求解思维流程例说
朱怀东
动态平衡问题是高考的重点.物体在缓慢移动过程中,均处于平衡状态,但物体所受的某些力的大小、方向均发生改变,使结果出现一些不确定性,这是此类问题常失分的主要因素.针对此类问题,只要按照以下思维流程,准确分析各力变化特点,合理选取解题方法,问题便可迎刃而解.
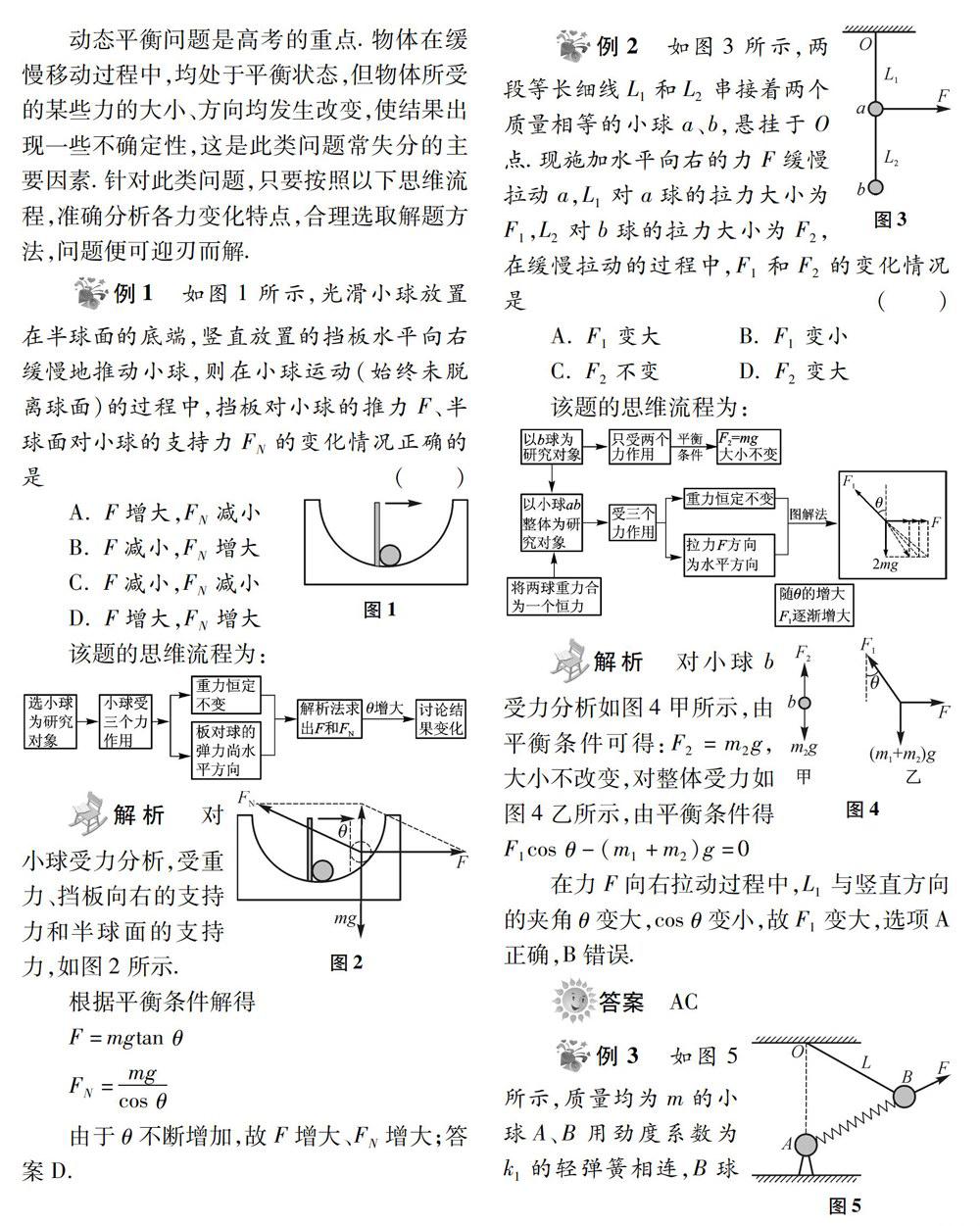
例1 如图1所示,光滑小球放置在半球面的底端,竖直放置的挡板水平向右缓慢地推动小球,则在小球运动(始终未脱离球面)的过程中,挡板对小球的推力F、半球面对小球的支持力FN的变化情况正确的是 ()
A.F增大,FN减小
B.F减小,FN增大
C.F减小,FN减小
D.F增大,FN增大
该题的思维流程为:
解析 对小球受力分析,受重力、挡板向右的支持力和半球面的支持力,如图2所示,
根据平衡条件解得
F= mgtan θ
FN=ng/cosθ
由于θ不断增加,故F增大、FN增大;答案D.
例2 如图3所示,两段等长细线L1和L2串接着两个质量相等的小球a、b,悬挂于O点.现施加水平向右的力F缓慢拉动a,L1对a球的拉力大小为F1,L2对b球的拉力大小为F2,在缓慢拉动的过程中,F1和F2的变化情况是
()
A.F1变大
B.F1变小
C.F2不变
D.F2变犬
该题的思维流程为:
解析 对小球6受力分析如图4甲所示,由平衡条件可得:F2=m2g,大小不改变,对整体受力如图4乙所示,由平衡条件得F1cosθ- (m1 +m2)g =0
在力F向右拉动过程中,L1与竖直方向的夹角θ变大,cos θ变小,故F1变大,选项A正确,B错误.
答案 AC
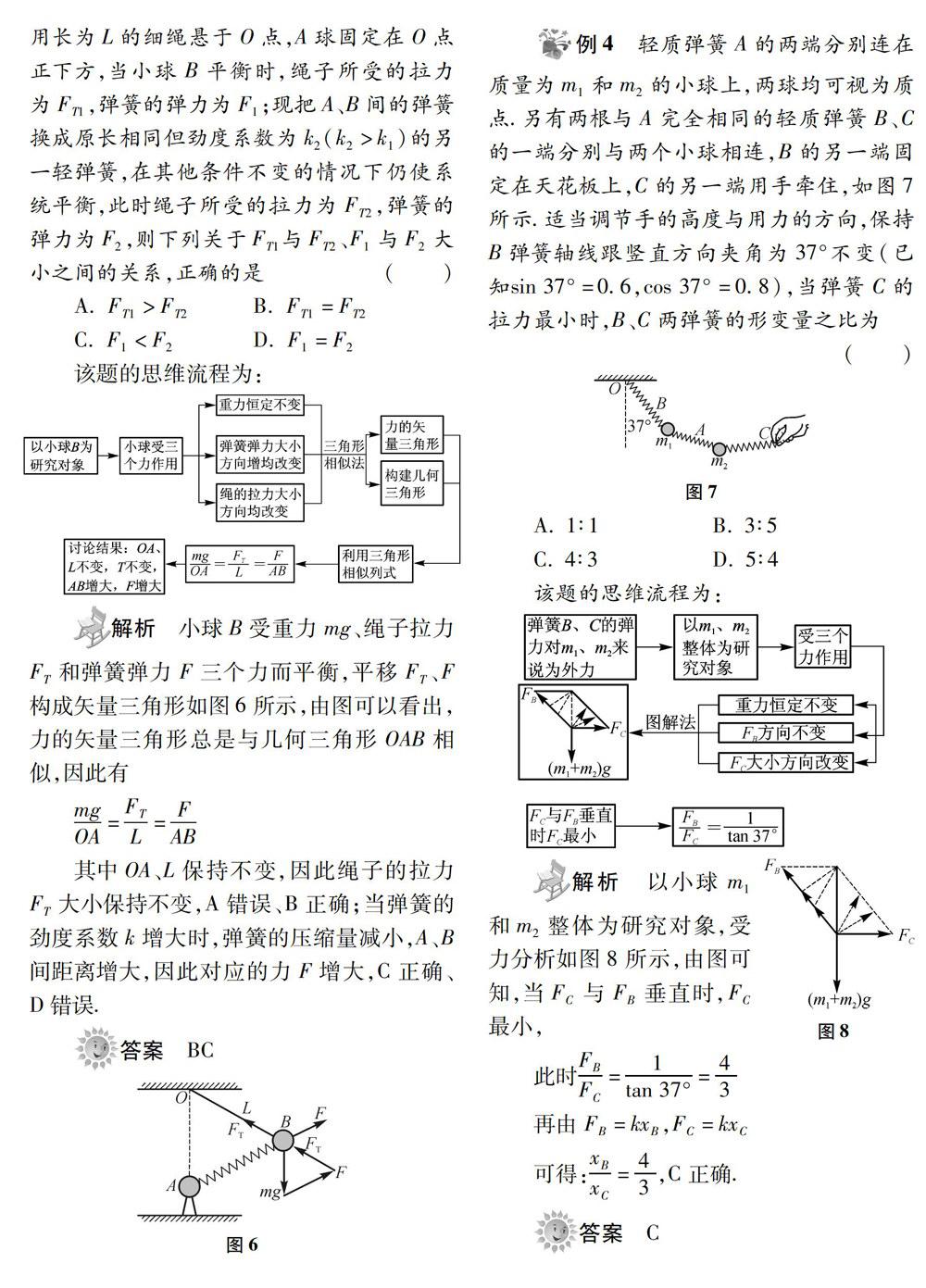
例3 如圖5所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,4球固定在O点正下方,当小球B平衡时,绳子所受的拉力为FT1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为FT2,弹簧的弹力为F2,则下列关于FT1与FT2、F1与F2大小之间的关系,正确的是
()
A.FT1>FT2
B.FT1=FT2
C.Fl< F2
D.Fl=F2
该题的思维流程为:
解析 小球B受重力mg、绳子拉力FT和弹簧弹力F三个力而平衡,平移FT、F构成矢量三角形如图6所示,由图可以看出,力的矢量三角形总是与几何三角形OAB相似,因此有 mg/OA=FFT/L=F/AB
其中OA、L保持不变,因此绳子的拉力FT大小保持不变,A错误、B正确;当弹簧的劲度系数k增大时,弹簧的压缩量减小,A、B间距离增大,因此对应的力F增大,C正确、D错误.
答案 BC
例4 轻质弹簧4的两端分别连在质量为m1和m2的小球上,两球均可视为质点.另有两根与A完全相同的轻质弹簧B、C的一端分别与两个小球相连,B的另一端固定在天花板上,C的另一端用手牵住,如图7所示.适当调节手的高度与用力的方向,保持B弹簧轴线跟竖直方向夹角为37°不变(已知sin 37°=0.6,cos 37°=0.8),当弹簧C的拉力最小时,B、C两弹簧的形变量之比为 ()
A.1:1
B.3:5
C.4:3
D.5:4
该题的思维流程为:
解析 以小球m1和m2整体为研究对象,受力分析如图8所示,由图可知,当FC与FB垂直时,FC最小,


动态平衡问题是高考的重点.物体在缓慢移动过程中,均处于平衡状态,但物体所受的某些力的大小、方向均发生改变,使结果出现一些不确定性,这是此类问题常失分的主要因素.针对此类问题,只要按照以下思维流程,准确分析各力变化特点,合理选取解题方法,问题便可迎刃而解.
例1 如图1所示,光滑小球放置在半球面的底端,竖直放置的挡板水平向右缓慢地推动小球,则在小球运动(始终未脱离球面)的过程中,挡板对小球的推力F、半球面对小球的支持力FN的变化情况正确的是 ()
A.F增大,FN减小
B.F减小,FN增大
C.F减小,FN减小
D.F增大,FN增大
该题的思维流程为:
解析 对小球受力分析,受重力、挡板向右的支持力和半球面的支持力,如图2所示,
根据平衡条件解得
F= mgtan θ
FN=ng/cosθ
由于θ不断增加,故F增大、FN增大;答案D.
例2 如图3所示,两段等长细线L1和L2串接着两个质量相等的小球a、b,悬挂于O点.现施加水平向右的力F缓慢拉动a,L1对a球的拉力大小为F1,L2对b球的拉力大小为F2,在缓慢拉动的过程中,F1和F2的变化情况是
()
A.F1变大
B.F1变小
C.F2不变
D.F2变犬
该题的思维流程为:
解析 对小球6受力分析如图4甲所示,由平衡条件可得:F2=m2g,大小不改变,对整体受力如图4乙所示,由平衡条件得F1cosθ- (m1 +m2)g =0
在力F向右拉动过程中,L1与竖直方向的夹角θ变大,cos θ变小,故F1变大,选项A正确,B错误.
答案 AC
例3 如圖5所示,质量均为m的小球A、B用劲度系数为k1的轻弹簧相连,B球用长为L的细绳悬于O点,4球固定在O点正下方,当小球B平衡时,绳子所受的拉力为FT1,弹簧的弹力为F1;现把A、B间的弹簧换成原长相同但劲度系数为k2(k2>k1)的另一轻弹簧,在其他条件不变的情况下仍使系统平衡,此时绳子所受的拉力为FT2,弹簧的弹力为F2,则下列关于FT1与FT2、F1与F2大小之间的关系,正确的是
()
A.FT1>FT2
B.FT1=FT2
C.Fl< F2
D.Fl=F2
该题的思维流程为:
解析 小球B受重力mg、绳子拉力FT和弹簧弹力F三个力而平衡,平移FT、F构成矢量三角形如图6所示,由图可以看出,力的矢量三角形总是与几何三角形OAB相似,因此有 mg/OA=FFT/L=F/AB
其中OA、L保持不变,因此绳子的拉力FT大小保持不变,A错误、B正确;当弹簧的劲度系数k增大时,弹簧的压缩量减小,A、B间距离增大,因此对应的力F增大,C正确、D错误.
答案 BC
例4 轻质弹簧4的两端分别连在质量为m1和m2的小球上,两球均可视为质点.另有两根与A完全相同的轻质弹簧B、C的一端分别与两个小球相连,B的另一端固定在天花板上,C的另一端用手牵住,如图7所示.适当调节手的高度与用力的方向,保持B弹簧轴线跟竖直方向夹角为37°不变(已知sin 37°=0.6,cos 37°=0.8),当弹簧C的拉力最小时,B、C两弹簧的形变量之比为 ()
A.1:1
B.3:5
C.4:3
D.5:4
该题的思维流程为:
解析 以小球m1和m2整体为研究对象,受力分析如图8所示,由图可知,当FC与FB垂直时,FC最小,

