浅谈概率论与数理统计的学习策略

    李云娟 樊雪双

    

    

    摘 要：本文主要介绍了《概率论与数理统计》课程中四个方面的学习策略，主要包括写章节知识网络图、总结概率类型、一题多解，改变题目的条件或结论同时对这四方面策略的使用进行举例说明。

    关键词：学习策略;知识结构图;概率题类型;一题多解

    一、绪论

    概率论与数理统计是一门研究随机现象的统计规律性和随机数据处理技术的数学学科[1]，其理论发展迅速，应用也极其广泛，这门课也是很多高校开设的核心数学课程之一，这门课程包括两部分，其中一部分是概率论，另一部分是数理统计，一般大学生来到高校之后首先学习的是《高等数学》这门课，学完之后部分专业学生会学习数学学科的其他数学课程，概率论与梳理统计就是其中一门数学课程，很多学生在学概率论与数理统计课程时会继续采用《高等数学》课程的思维方式去学习往往效果不理想，学生会感觉上课对知识的理解浅显，老师稍微换个表达方式就不理解，对于课后作业题目能阅读完，可是对题目的解决办法很茫然，当然更谈不上灵活运用，举一反三了，久而久之，学生出现厌烦这门课的心理状态，上课无法专心听讲，当然考试成绩也不理想，其实《概率论与数理统计》这门课程的理论与思维方式与《高等数学》不同，《高等数学》包含的基本上更多的是一种数学理论、推理和计算，而《概率论与数理统计》主要研究的是随机现象，学生经常反应学好《高等数学》不是很难，但是学好《概率论与数理统计》却是困难的，他们反映在学习这门课程时会感到力不从心，对知识的掌握不牢固，有时连题目读懂也有困难，尤其是概率这部分，概率类型多，做概率题时不知道用哪个概率公式，理不清头绪，考试过关率低。学生之所以出现这些情况并不是学生智商低，学习不努力，关键是学生没有找到适合这门课程的学习策略，孙建平等人在概率论与数理统计学习策略的统计分析论文中采用问卷调查和考试的方法进行调查分析，研究了学习策略对概率论与数理统计学习成绩的影响。结果发现，学习策略和概率论与数理统计学习成绩密切相关，学习策略对概率论与数理统计学习成绩影响显著[2]，有效的学习策略会使得学生学习效率提高，增强学生学习信心，使得学生喜欢上这门课程。

    二、数学学习策略

    数学学习策略指的是在数学学习情境中，学生根据自身情况和对数学学习目标的认识，控制数学学习过程，优化数学学习方法，整合数学学习活动，提高数学学习效率的系统的学习过程[3]。

    三、概率论与数理统计的学习策略

    本文根据学生学习状况及数学学习策略以及自己多年的教学经验从一名教师的视角出发提出以下四种学习《概率论与梳理统计》的学习策略：

    （一）编写知识结构图

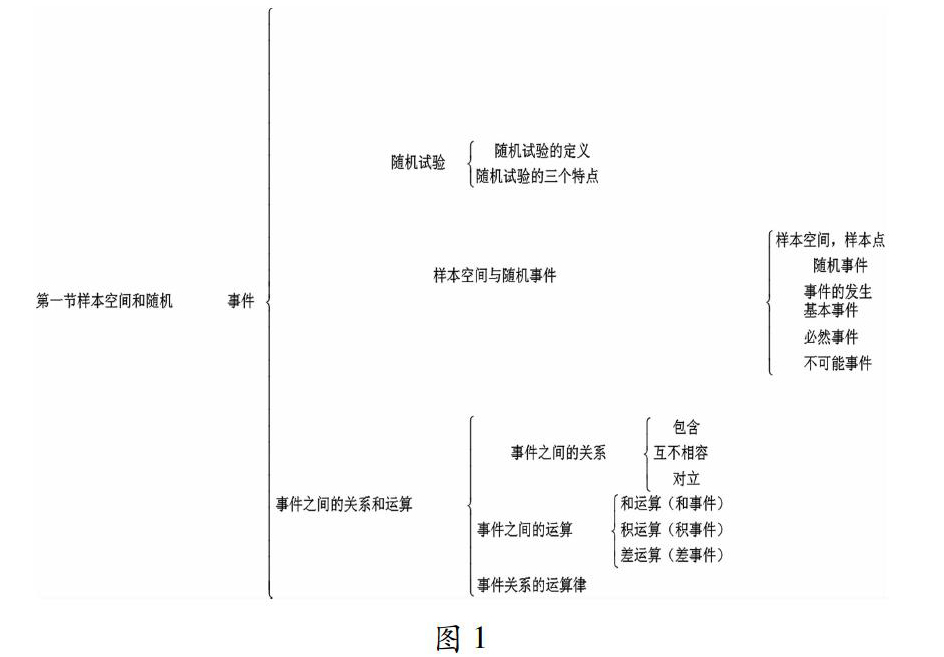
    知识结构图是指把所学内容进行整理并制成比较系统完整的知识结构图示。知识结构的整理与展示可以帮助学生梳理知识，增强学生对知识之间内在联系的理解。概率论知识在最初几节里主要介绍基本概念、公式，后面章节主要介绍一些事件概率的计算方法。这里内容繁杂，如果采用编写知识结构图的方法对这些知识进行梳理，可以使繁杂的知识条理化，有助于理解记忆知识点，减轻学生学习的负担。知识结构图可以是每一节的，也可以是每一章，或者是一本书的，大家可以按照书上章节大标题及里面的小标题编写知识结构图，也可以自己根据知识之间的关系按照自己的目的和要求进行编写。下图是概率论与数理统计的第一节样本空间、随机事件的知识结构图（图1）。

    （二）对概率问题进行总结归类

    《概率论与数理统计》第一章里介绍了很多种类型概率问题，学生在学习时会一知半解，再加上概率题类型多，学生就更容易混淆，因此在这部分内容里面学生需要先弄清各種类型概率的定义，然后抓住其本质特点进行总结归类，可以从问题入手寻找解决办法：

    1.条件概率的适用条件

    条件概率的定义：设A、B为两事件，P（B）>0，则称P（AB）/P（B）为事件B发生的条件下事件A发生的条件概率，记为P（A|B）=P（AB）P（B）如果问题中出现在事件A发生的情况下事件B发生的概率可以考虑用条件概率：

    例1：某批产品共100件，其中有8件是不合格产品，而8件不合格产品中又有5件是次品，3件是废品，今从100件产品中任取一件已知抽到的是不合格品，求它是废品的概率。

    分析：问题可叙述成在抽到的产品为不合格产品的情况下是废品的概率，所以考虑用条件概率公式。

    2.乘法公式适用的条件

    乘法公式定义：P（AB）=P（A）PBA（P（A）>0），根据乘法公式定义，判断出乘法公式是求积事件的概率，因此如果问题出现求两个事件同时发生的概率则考虑用乘法公式

    例2 某批产品中，甲厂生产的产品占60%，甲厂的产品的次品率为10%，从这批批产品中随意的抽取一件，求该产品是甲厂生产的次品的概率。

    分析：问题为该产品是甲厂生产的次品率，即就是既要是甲厂生产的产品同时还要是次品，说明是两件事同时发生，所以考虑用乘法公式。

    解：A：从这批产品中随意的抽取一件产品是甲厂生产的

    B：从这批产品中随意的抽取一件产品是次品

    3.贝努里概型公式的适用条件

    如果出现做n次实验，事件A发生K次的概率则可以考虑用贝努里概型公式Pn（k）=Cknpk（1-p）n-k。

    例3 某彩票每周开奖一次，每一次提供十万分之一的中奖机会，若你每周买一张彩票，尽管你坚持十年（每年52周）之久，你从未中过一次奖的概率是多少？

    分析：按假设，每次中奖的概率是10-5，于是每次未中奖的概率是1-10-5，每周买一张彩票，坚持十年（每年52周），十年共购买彩票520次，每次开奖都是相互独立的，从未中过一次奖指中奖0次，即要计算做实验520次，事件发生0次的概率，则可以考虑采用贝努里概型公式。

    解：十年中未中过奖（每次都未中奖）的概率是：

    （三）尝试一题多解

    一题多解可以帮助学生扎实的掌握的知识点，提高学生多角度、多层次分析问题的能力，进而达到对问题的全面理解，迅速而准确的解决问题的目的。下面来举例说明：

    例4 设在一个盒子里装有10只晶体管，4只是次品，6只是正品，在其中取两次，每次任取一只，做不放回抽样，问两次都取到正品的概率是多少？

    分析：问题为两次都取正品的概率，说明是两件事同时发生所以考虑用乘法公式，这就是解法1;另外这还是一个古典概型，所以也可以考虑用古典概型公式去解决，即就是解法2。

    解法1：设A：第一次取到的是正品晶体管

    （四）尝试改变题目的条件或结论

    学生在做《概率论与数理统计》这门课程的练习题时可以在做完原题的基础上尝试改变题目的条件或者结论，使得原先的一道题变成多到题，然后试图用学过的方法来解决，学生做这种被改变的题目时就需要多看书多分析知识点之间的差别，多注意题型的变化，学生经常做这样的训练将会对知识点掌握的更加牢固，解决问题方法也将更灵活。

    例4：某厂生产一批灯泡共100只，其中有6只是不合格产品，而6只不合格产品中又有4只是次品，2只是废品，今从100只灯泡中任取一只：

    （1）求抽到的灯泡是废品的概率。

    （2）已知抽到的灯泡是不合格品，求它是废品的概率。

    此题一共有两问，第一问是古典概型可用古典概型公式，第一问可改成下面的题目抽到的是次品的概率，还可改成抽到的是合格品的概率是多少，改变之后的两道题也是采用古典概型公式就可以解决的，这样一道题就可以改编成2道题目，而且学生对于古典概型掌握的将更加熟练;第二问采用条件概率公式，该题改编成已知抽到的灯泡是不合格品，求它是次品的概率，改变之后也可以采用条件概率公式。

    四、结语

    《概率论与数理统计》这门课程在大学里是一门较难掌握的科目，本文介绍了这门课程的四个方面的学习策略，分别是编写思维导图，总结归类，一题多解和尝试改变题目的条件和结论，同时本文还通过进行举例和分析来说明这四个策略的具体使用方法。

    参考文献：

    [1]黎协锐，谭伟明.概率论与数理统计.航空工业出版社，2017.

    [2]孙建平，吕效国，陆利平.概率论与数理统计学习策略的统计分析.高师理科学刊，2011.

    [3]白雪.高一学生数学学习策略的调查研究——以阜新市H和S高中为例[D].沈阳师范大学，2017.

    项目：感谢西安思源学院2020年精品在線开放课程校级项目概率论与数理统计的支持