一种改进的点云数据组合精简算法
尹星翔 唐平 黄永慧 钟灵


摘要:在逆向工程中,点云数据的精简是一个重要的步骤,精简的质量直接关系到后续曲面重构的效率。文章针对广州灰塑曲率较大,凹凸面较多的特点,提出了一种基于曲率和均匀精简的点云数据精简方法:利用包围盒法对散乱的点云数据进行拓扑规则排序,建立点的K-邻域集,计算点云在某点处的曲率,在曲率较大处保留更多的特征点,但是曲率较小处会删除较多的点云数据。文章在此基础上再利用均匀网格的方法对初始精简后的点云进行重采样处理,使得曲率较小处的特征点也能保留下来。
关键词:逆向工程;灰塑;曲率;均匀精简;点云数据;K-邻域
随着三维数据采集设备的日益发展和计算机技术的不断成熟,文物保护工作者可以方便而精准地获取文物的三维物体表面数据点云信息。广州灰塑作为非物质文化遗产的一部分,更应好好保护。在与广州灰塑文化研究院合作的项目(广州市花都区科技计划项目)中发现灰塑点云数据的采集有如下的特点:灰塑作品种类繁多、体积较大,采集到的点云数据极为庞大,单个作品的点云数量级达到百万以上。在三角剖分中,由于过密点云结构的三角面片模型过于庞大,传输、显示或处理都将消耗大量的时间和计算机资源;在曲面重构时,过密的点云不但计算量大,而且可能影响其光顺性及存储。因此,如何在保持测量对象信息的情况下对测量点进行最大程度地精简,对于准确、快速地点云预处理或其他的后续工作非常重要。
国内外对点云精简的研究,已经有了很多研究成果。刘涛提出了一种基于包围盒法的散乱点云数据的曲率精简,该方法虽然对特征点保留得很好,但是对曲率较小的平滑区域剔除的点云数据太多,不利于模型后续的三维重建。程效军等提出了基于自适应八叉树的点云数据压缩方法,该方法能较好地保留点云数据的细节和轮廓特征,但是构建八叉树的过程较复杂,且一些经验阈值(如包围盒的大小)的设定也尚待改进。
经过对各种精简算法的比较,结合灰塑的种类繁多的特点,即有的凹凸不平(平均曲率值较大),有的较光顺(平均曲率较小),文章提出了一种基于曲率和均匀精简的点云数据精简方法,核心思想是基于包围盒来建立K-邻域,求出整个点云数据的平均曲率,根据曲率精简原则选取特征点云,然后针对曲率较小处空白较多的问题采用均匀精简方法。首先,基于曲率的精简算法对处理曲率变化较大的点云数据优势明显,其次,均匀精简算法能保留曲率较小处的特征点,避免空白区域的产生,且算法原理简单。
1 改进的点云数据组合精简算法
算法的基本思想:
(1)将原始点云利用包围盒法进行剖分,确立每个K-邻域的中心点,并对所有中心点的K-邻域完成搜索。计算邻域内的曲率并依照曲率精简原则对点云进行精简,曲率较大处保留较多点云,曲率较小处点云精简多一些。
(2)对基于曲率精简中被剔除的点进行重采样,将点云数据划分到栅格中,每个栅格中保留距离栅格中心距离最近的点,然后将保留下来的点加入第一步保留的点中,最终得到精简后的点云。
1.1 基于包围盒法建立K-邻域
论文中原始点云数据分布没有规律性,缺少明显的几何拓扑关系。因此,需要建立点云的拓扑关系来提高精简点云的效率,这里采用包围盒法来对点云进行剖分并建立K-邻域。包围盒法建立K-邻域的方法参照文献,文章在此不作详述。
点云数据在X,Y,Z方向上的最值Xmin,Xmax,Ymin,Ymax,Zmin,Zmax,设n为选取点云的总个数,其值根据点云的分布情况和密集程度选取,一般为24~32时可以达到精度要求,文章中由于点云数据较密集,n取32,则自适应的包围盒大小为:(1)
包围盒个数:设X在轴方向上,包围盒个数为Nx,则
Nx=ceil[(Xmax-Xmin)/S0]
同理,沿着X轴和y轴方向的包围盒个数为分别为
Ny=ceil[(Ymax-Ymin)/S0]
Nz=ceil[(Zmax-Zmin)/S0]
所以总的包围盒个数为Nmax=NxNyNz
通过上述步骤取的32个点利用最小二乘法来拟合二次曲面,二次曲面方程如(2)式所示。(2)
1.2 基于曲率的点云数据精简
1.2.1 曲率的计算
由(2)式建立的拟合方程,根据最小二乘原理求出拟合方程的系数,即要使下式取得最小值:(3)
(3)式中xk,yk,zk邻域内数据点的坐标值,将式(3)分别对系数求导,并使其等于0:(4)
根据(4)式求出拟合方程系数ci,j-i。
求出系数之后,文章求出数据点的平均曲率,二次曲面函数的一阶和二阶微商表示如下:(5)则曲面的平均曲率可由曲面函数的微商表示为(6)
重复以上步骤,求出所有选取点在该邻域内的平均曲率Pi,然后计算出整个点云数据所有点的曲率平均值:(7)
1.2.2 曲率精简准则
由微分几何可知,平均曲率是曲面弯曲程度的测量标准,因此可以用平均曲率来作为点云数据的精简准则。若该点的平均曲率Pi≤p,则说明该点在它的K-邻域内属于分布较平坦的点,删除该点;反之,则说明该点在它的K-邻域内属于分布较尖锐的点,保留该点。重复该步骤,直到所有点的曲率比较完成这个过程。
1.3 均匀精简
在1.2节基于曲率的点云精简过程中,点云中位于较平坦区域的大部分数据点会因为曲率较小而被精简掉,这样会导致点云数据平坦区域留有一片空白,丢失很多模型的几何特征,如图1所示。
这些空白区域会影响后续建模的质量,导致模型不够完整,特征点丢失较多。为了在基于曲率精简的基础上尽可能多地保留特征点,本文提出了一种基于曲率和均匀精简的混合精简算法,有效地解决了这个问题。
均匀精简法的思想流程是把所有点云数据都封闭在一个大的长方体之中,然后根据精简百分比将这个长方体划分为m×n×l(m,n,l的值见下文)个边长相等的小立方体,在每个小立方体中取离立方体中心点最近的点云数据作为特征点,如图2所示。
这种方法单独使用会存在一定的缺陷:在模型曲率较大处会损失很多几何特征点。但是与基于曲率的初始精简相结合,就能弥补平坦区域空白的产生,相互克服各自的缺点。
均匀精简具体算法流程如下:
(1)将在初始精简中被删除的点读入,求出这些点数据在X,Y,Z方向上的最值Xmin,Xmax,Ymin,Ymax,Zmin,Zmax。
(2)按照精简百分比需要确定小立方体包围盒边长s,将大长方体在X,Y, Z方向上分别分割成m,n,l个小立方体,其中
m=(int)[(xmax-xmin)/s+1]
n=(int)[(ymax-ymin)/s+1] (8)
l=(int)[(zmax-zmin)/s+1]
(3)将点云中所有点按其三维坐标划分到不同的小立方体中,点P0(x0,y0,z0)所在的立方体空间位置索引为xIndex,yIndex,ZIndex,则
xIndex=(int)[(x0-xmin)/s]
yIndex=(int)[(y0-ymin)/s] (9)
zIndex=(int)[(z0-zmin)/s]
(4)对每一个小立方体,求出其内部所有点到其中心的空间距离并进行排序,取距离中心最近的点并保留,其余的点将被作为精简点。其中索引位置(xIndex,yIndex,zIndex),的立方体方格的中心位置(z,y,z)的计算公式为:
x=xmin+(0.5+xIndex)×s
y=ymin+(0.5+yIndex)×s
z=zmin+(0.5+zIndex)×s (10)
1.4 本文算法的点云精简流程
综上所述,点云数据总体的精简步骤的流程图如图3所示。
2 实验结果
2.1 实验环境
如图4所示为广州市花都区灰塑文化研究院提供的灰塑作品一木棉花开(以下简称盘子)来进行三维扫描,获得实验的数据来源。
2.2 实验结果
在精简的比例约为93%的前提下,用3种不同的精简方法,对比所得实验结果,验证文章中方法的有效性。
试验环境:Windows7 64位操作系统,CPU为酷睿i5-3210M 2.5GHz双核,内存为4GB,显卡为GT645M,仿真环境Matlab2010b。
如图5所示为盘子经过三维扫描仪扫描得到原始点云数据,点云总数为428532;图6是仅采用基于曲率算法精简的结果;图7是仅采用均匀精简算法精简的结果,其中立方体栅格边长取s=30.0μm;图8是文章中的组合算法精简的结果。
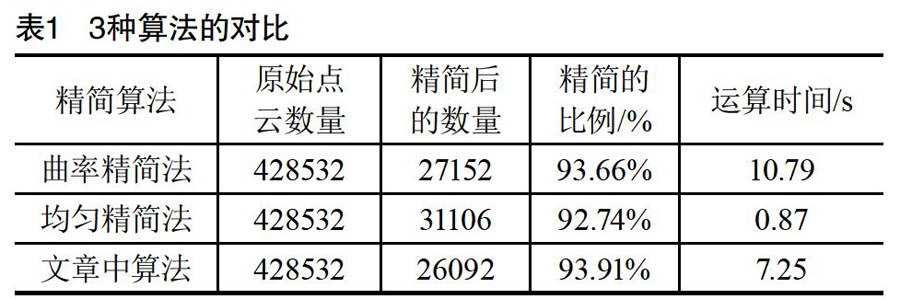
表1所示为3种算法的结果对比。
从精简结果可以看出,相比于曲率精简,文章中的算法在平坦处保留了较多的点,避免了空白区域的产生,而且算法运行速度也更快了;相比于均匀精简,文章中的算法保留了更多的特征点。将两种算法组合起来,既能够保留点云数据的特征区域,又有效地降低了时间复杂度,整体精简效果比较好。
3 结语
对于海量散乱点云数据的处理工作,点云数据的精简是一个重要的环节。在与广州灰塑文化研究院合作的项目中,文章分析了现有的散乱点云数据精简算法,在此基础上针对灰塑文化作品的曲率较大、凹凸面较多的特点,提出了一种基于曲率和均匀精简的点云数据精简方法。曲率精简法在保留特征点方面有优势,但是在平坦区域会产生空白区域;均匀精简法在保留特征点处存在很大缺陷。文章针对这两种算法的优点和缺点,进行了算法整合,原理简单明了,虽然相应的处理速度变慢了,但是获得的精简效果是非常好的。

