狭义与广义相对论探讨（三）

    

    

    

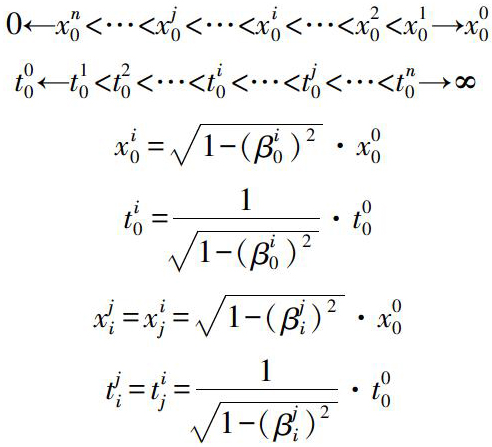
    摘?要：首次根据爱因斯坦提出的尺缩钟慢效应，扩展出同地异时、同时异地、异地异时随机事件的空间间隔和时间间隔在动系与静系中变化的数学函数表达式，指出这种情况下，时间和空间是相互独立的。首次提出了等长的刚性量杆和等时的惯性系原点上的同步钟的原长和原时在所有的不同惯性系中都是相等的。首次提出了，当无数惯性系的原点连续连接时的轨迹，和牛顿力学的质点在静系中的运动轨迹是一样的。首次提出了，任何参考系都和静系是平权的，可以是匀速、变速、加速、减速、规则、不规则的;可以由一维扩展到二维和三维空间，其运动轨迹可以是任意形状的非闭合曲线和任意形状的闭合曲线。首次提出对撞机的理论依据是错误的。首次提出了隧道佯谬、车库佯谬、孪生子佯谬是错误的。

    关键词：原长;原时;尺缩钟慢效应

    狭义相对论中最著名的效应是动尺变短和动钟变慢，即尺缩钟慢效应，下面我们看看，爱因斯坦是怎样阐述的。

    1 尺缩效应

    爱因斯坦《狭义与广义相对论浅说》北京大学出版社科学元典从书/彩图珍藏版28页《量杆和钟在运动时的行为》是这样讲的：

    我沿着K′的x′轴放置一根米尺，令其一端（始端）與点x′=0重合，另一端（末端）与点x′=1重合。问米尺相对于参考系K的长度为何？要知道这个长度，我们只须求出在参考系K的某一特定时刻t、米尺的始端和末端相对于K的位置。借助于洛伦兹变换第一方程，该两点在时刻t=0的值可表示为两点间的距离为：

    两点间的距离为：

    但米尺相对于K以速度v运动。因此，沿着其本身长度的方向以速度v运动的刚性米尺的长度为：

    米。因此刚尺在运动时比在静止时短，而且运动得越快刚尺就越短。

    这就是爱因斯坦讲的尺缩效应的原始文献，我们还原他的推导过程：

    这个式子对于沿着K′的x′轴放置的一根米尺的任意长度都是适用的，因为运动不会改变参考系本身的空间间隔，所以对于K′的x′轴上的每一点的空间坐标都是适用的，任何时间都一样，就是说，与时间没有关系。

    接着，爱因斯坦说：反之，如果我们所考察的是相对于K静止在x轴上的一根米尺，我们就应该发现，当从K′去判断时，米尺的长度是：

    这与相对性原理完全相合，而相对性原理是我们进行考察的基础。同样，我们可以证明，当t′=0时：

    这个式子对于沿着K的x轴放置的一根米尺的任意长度都是适用的，因为运动不会改变参考系本身的空间间隔，所以对于K的x轴上的每一点的空间坐标都是适用的，任何时间都一样，就是说，与时间没有关系。

    2 钟慢效应

    文章的后半部分是叙述钟的，爱因斯坦说：我们现在考虑永久放在K′的原点（x′=0）上的一个按秒报时的钟。t′=0和t′=1对应于该钟接连两声嘀嗒。对于这两次嘀嗒，洛伦兹变换的第一和第四方程给出：

    从K去判断，该钟以速度v运动;从这个参考物体去判断，该钟两次嘀嗒之间所经过的时间不是1秒，而是：11-v2c2秒，亦即比1秒钟长一些。该钟因运动而比静止时走得慢了。

    这也是爱因斯坦讲的钟慢效应的原始文献，我们还原他的推导过程：

    因为，任一时间，同一参考系的所有时空点都是等时的，这个式子对于K′的x′轴上的任意一点的时间坐标都是适用的，又因为运动不会改变参考系本身的时间间隔，所以对于K′的x′轴上的每一点的空间坐标都是适用的，任何空间都一样，就是说，与空间没有关系。

    同样，如果我们所考察的是相对于K静止在x轴原点上的钟时，x=0，我们就应该发现，当从K′去判断时，时间的间隔是：

    因为，任一时间，同一参考系的所有时空点都是等时的，这个式子对于K的x轴上的任意一点的时间坐标都是适用的，又因为运动不会改变参考系本身的时间间隔，所以对于K的x轴上的每一点的空间坐标都是适用的，任何空间都一样，就是说，与空间没有关系。

    3 结论

    3.1 随机事件

    对于同时异地、同地异时、异地异时等空间间隔和时间间隔没有速度关联的随机事件，在任一惯性参考系中，空间和时间是绝对的，没有联系的;在两个惯性参考系中，空间和时间的变化遵循相对性原理：

    3.2 质点事件

    对于和速度关联的质点事件，我们只考虑直线运动，在只关注起点和终点的情况下，不管它是匀速的还是变速的，变化是规则的还是不规则的，空间间隔和时间间隔，在任一惯性参考系中，空间和时间也是绝对的，规则的和速度与加速度有确切的关系，不规则的则没有确切的关系;在两个惯性参考系中，空间和时间的变化遵循相对性原理：

    当质点做匀速运动时：

    它们在两个惯性参考系中的速度也遵循相对性原理。

    3.3 时空间隔不变性

    公式没有意义，时空间隔不变性不成立，由此推出的闵可夫斯基四维时空、光锥、类时时空、类空时空、史瓦西时空、黑洞、虫洞、宇宙大爆炸等，都是不存在的。

    3.4 时序和因果关系

    因为x和x′，t和t′永远为一元一次正比例函数的关系，所以x和x′，t和t′永远是保时序的，永远不会发生因果颠倒的情况。

    3.5 诡异的相对性原理

    我们只考虑惯性系中放于原点的等长的刚性量杆和等时的同步的钟，设：

    这里，上标表示物理量所在的惯性系，下标表示物理量相对的惯性系。0表示静系，正整数n表示动系。上下标相同的x表示刚性量杆在该惯性系的原长，上下标相同的t表示原点同步钟在该惯性系的原时。

    我们可以得到这样的结论：

    （1）相同长度的刚性量杆，在所有惯性系的原长都相同，并且没有变化，都等于量杆在静系中的长度。

    （2）相同时间的原点同步钟，在所有惯性系的原时都相同，并且没有变化，都等于钟在静系中的时间。

    《浅说》213页《论动体的电动力学》《关于长度和时间的相对性》中，爱因斯坦说“设有一静止的刚性杆;用一根也是静止的量杆量得它的长度是l。我们现在设想这杆的轴是放在静止坐标系的X轴上，然后使这根杆沿着X轴向x增加的方向作匀速的平行移动（速度是v）。我们现在来考查这根运动着的杆的长度，观察者同前面所给的量杆以及那根要量度的杆一道运动，并且直接用量杆同杆相叠合来量出杆的长度，正像要量的杆、观察者和量杆都处于静止时一样。这样求得的长度，我们可称之为“动系中杆的长度”。根据相对性原理，它必定等于静止杆的长度l.”可以作为结论（1）的佐证。根据时空的均匀性和空间的各向同性性，可以证明结论（2）也是正确的。

    （3）运动时变化的是，原长和原时在其他惯性系的空间间隔和时间间隔。

    （4）当n趋于无穷大时，这样的变化有无穷多。根据相对性原理，互为对应的两个惯性系中的空间、时间和牵连速度的变化，永远都是相等的。

    （5）当v由0趋于c时，x′由x趋于0，t′由t趋于无穷大。

    （6）当Δv趋于0，x无限接近于原点时，坐标系原点的变化，变为质点在静系中的加速运动轨迹，加速度不要求相同，可以是规则变化，也可以是不规则变化，“质点”的“原长”和“原时”，均与静系中对应的“原长”和“原时”相一致，即“质点”的运动轨迹就是静系中牛顿力学的运动轨迹。

    （7）根据前面的数学表达式，牵连速度相反的变化，也有类似的结果，即当v由c趋于0时，x′由0趋于x，t′由∞趋于t;当Δv趋于0，x无限接近于原点时，坐标系原点的变化，变为质点在静系中的减速运动轨迹，减速度不要求相同，可以是规则变化，也可以是不规则变化，“质点”的“原长”和“原时”，均与静系中对应的“原长”和“原时”相一致，即“质点”的运动轨迹就是静系中牛顿力学的运动轨迹。这样就证明了，牛顿力学质点在一维空间即X正半轴上的所有运动轨迹，和爱因斯坦相对论动系原点的连续变化的运动轨迹，完全一致，并且不仅仅限于惯性系，可以是任意参考系，可以是匀速的、变速的、加速的、减速的、规则变化的、不规则变化的、可以从静止开始、可以至静止结束。

    （8）因为，对于刚性量杆和原点同步钟，空间间隔和时间间隔是相互独立的，所以，可以将一维空间的结论，扩展到二维平面空间，这样，质点的轨迹可以是直线、折线、曲线、规则的线、不规则的线、规则的闭合曲线、不规则的闭合曲线，包括圆周运动。

    （9）同理，可以将二维平面空间，扩展到三维立体空间，质点的运动轨迹就包括了所有的牛顿力学的三维轨迹，包括封闭的螺旋曲线圆周运动，即宏观的天体运行轨迹及微观粒子的运行轨迹，完全和牛顿力学符合，没有爱因斯坦所说的尺缩效应、钟慢效应、质能效应等。就是说，对撞机的理论根据是错误的。

    （10）爱因斯坦的尺缩钟慢效应只出现在在静系中观察动系中时空坐标的情况，并且不是所谓的视觉效果，什么在地面看空中的飞机变小了，太空的星体变扁了，远处的高铁跑的像蜗牛一样慢，等等。它们只是计算出来的，并且是无穷无尽的，因为，任何运动的物体，都可以在静系中拥有相对的时空坐标。

    （11）隧道佯谬。一列火车通过等长的隧道，在火车上看，隧道缩短了，可以在车头和车尾同时发射炮弹，而不会破坏隧道。在隧道看来，火车的车厢缩短了，可以将出口和进口的闸门同时放下，而不被中间的火车撞飞。根据相对性原理，两种情况都成立。根据逻辑推理，只能有一种情况发生。问这是悖论，还是佯谬。

    根据辩证唯物主义，矛盾双方是同时存在，同时进行的，没有单独的矛，也没有单独的盾。火车惯性系和隧道惯性系是平权的，火车看隧道的缩短和隧道看火车的缩短是同时存在的，因为它们的原长相等，牵连速度相等，所以长度的缩短值也相等，车头到达出口时，车尾刚好到达进口。所以，火车不能同时发射炮弹，隧道也不能同时放下闸门。上面的结论是悖论，不是佯谬。

    《浅说》109页《洛伦兹变化的简单推导》中，爱因斯坦在两个惯性系中分别给对方拍“快照”，然后说，这两个快照必须是全等的，可以佐证。

    （12）车库佯谬。儿子考上了北京大学，父亲买了一辆名牌车作为奖赏，回来后发现，家里的车库短了一些。父亲说，还得改造一下。儿子说，用不着，爱因斯坦说运动时物体的长度会缩短，只要我把速度提高到一定程度就可以了。父亲问，能缩短多少。想多短就多短，儿子说，将来科学技术发达了，如果接近亚光速，放多少辆车都可以。根据相对性原理，这种说法是正确的，请问这是悖论，还是佯谬。

    根据爱因斯坦的理论，运动不会改变惯性系刚性物体的原长，因此，不管牵连速度有多大，车尾到达车库进口的时候，车头总是超出车库相同的二者原长的差。因此，上述说法是悖论，不是佯谬。

    3.6 光子事件

    光子只是质点的特例，同样遵循质点的运动规律，这样，光子在两个惯性参考系中的速度也遵循相对性原理：

    因为，根据光速不变原理c=c′，当且仅当，惯性系牵连速度v=0时，上面的关系式才能成立，就是说，这样的惯性系根本就不存在，爱因斯坦的相对论时空观根本就不存在，洛伦兹变换是错误的，尺缩和钟慢效应是错误的。

    3.7 三胞胎悖论的答案

    前面我们证明，相对性原理，不仅仅适用于惯性系，任何参考系都适用，即匀速的、变速的、加速的、减速的、规则变化的、不规则变化的参考系，和静止参考系都是平权的。不仅仅适用于一维空间，也适用于二维和三维空间。当参考系的原点连续变化时，原点的运动轨迹和质点在静系中的牛顿力学运动轨迹是平权的，包括参考系从静系中出发，最后又返回到静系。因此，三兄弟的年龄是相等的，环球宇宙航行的二兄弟并没有比留在地面的老大年轻，他们的岁数是一样的。

    参考文献：

    [1][美]爱因斯坦著，杨润殷译.狭义与广义相对论浅说（科学元典丛书/彩图珍藏版）[M].北京：北京大学出版社，2019：1-32，109-115，209-228.

    [2][美]爱因斯坦著，范岱年等译.爱因斯坦文集（增补本）：第二卷[M].北京：商务印书馆，2017：92-126.

    [3]周培源.理論力学[M].北京：科学出版社，2019.

    [4]华罗庚.华罗庚文集·多复变函数论卷二[M].北京：科学出版社，2018：91-113.

    [5]梁灿彬，周彬.微分几何入门与广义相对论（上册·第二版）[M].北京：科学出版社，2019.

    [6]刘辽，赵峥.广义相对论（第二版）[M].北京：高等教育出版社，2018.

    [7]俞允强.广义相对论引论（第二版）[M].北京：北京大学出版社，2019.

    [8]刘海军.光速不变原理与洛伦兹变换[J].科技风，2020.

    [9]刘海军.狭义相对论探讨（一）[J].科技风，2020.

    [10]刘海军.狭义相对论探讨（二）[J].科技风，2020.

    作者简介：刘海军（1965—?），男，山西昔阳三都乡西峪村人，高级工程师，1986年广州华南理工大学化学系毕业后分配到山西省化工研究所工作至今，山西省化工研究所对外交流部科室，从事橡塑助剂英语编译。