“可能还是确定”
卫茂桦 肖 平
“可能还是确定”属于初中概率与统计领域中的内容,是七年级数学继“数据的收集”与“数据的表示”之后的一个学习内容,它是从学生周围熟悉的问题入手,让学生置身于解决一些简单的实际问题的过程,体会数据的作用,感受大千世界的不确定性,进一步熟悉收集、整理、描述和分析数据的活动过程,理解频数、频率、不可能发生、可能发生和必然发生的概念,使用的教材是华师大版七年级下册第11章第一节“可能还是确定”。
教学过程
1创设情境,激发兴趣
情境投影:2008年5月12日四川省汶川县发生8.0级强烈地震,这次地震波及范围广,持续时间长,破坏性特别大,造成我国数百万同胞无家可归,给我们国家造成巨大的损失……
教师:通过这次地震,我想大家肯定对地震的发生和预防有了一个全新的认识,你能回答下面几个问题吗?
①在地震发生以前,我们是否能够确定地震发生的具体时间、地点和震级呢?
②地震的发生是一个必然事件、可能事件还是不可能事件呢?
③有人预测:重庆市近些年来没有发生过地震,以后也不会发生地震,也有人预测:前两天发生了余震,所以今天也一定会有余震,这些说法是否正确?为什么?
(话音刚落)学生顿时议论纷纷,
教师:(引入课题)同学们肯定对这件事很关注,也很想知道到底是怎样的,大家的猜测到底对不对呢?通过这节课的学习,大家就能够准确地回答以上的问题(板书:可能还是确定)!
(学生十分投入,热情很高)
点评:把学生感兴趣的、经历过的情境移植到数学课堂,易于激发学生的学习兴趣,使其产生跃跃欲试的探索意识,产生主动求知的心理冲动,为学生的自主学习和独立探索营造良好的氛围。
2探索新知
教师:下面我们来做一个掷骰子游戏,两位同学为一组,一位同学掷骰子20次,另一位同学记录,并完成表格,
(学生在分组实验时,教师走下讲台巡视、指导学生正确操作,鼓励学生相互协作、相互配合,共同完成活动)
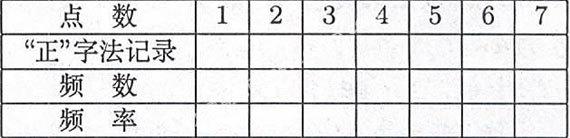
教师:点数为7的频数是多少?频率是多少?
学生1:点数为7的频数是0,频率也是0。
教师(追问):若把掷骰子的次数改成100次,甚至更多,点数为7的频数及频率会不会发生变化?为什么?
学生1:不会变化,因为不可能掷出7这个点数,与掷骰子次数无关,
教师:很好,分析得很透彻,若在以上游戏中填表的点数一栏增加“点数小于7”和“点数不小于7”两栏,则不用实验我们就可以知道“点数小于7”的频数及频率,它们分别是多少?
学生2:点数小于7的频数是20,频率是100%。
教师(追问):为什么不需实验我们就可以知道?
学生2:因为掷出的点数都是小于7的(有的学生在下面小声地说发生的可能性是100%)。
教师:回答得很正确,在这个游戏中,掷得点数为3的频数各小组相同吗?
学生四周张望相邻小组的实验数据,都摇头表示不相同。
教师:在未掷骰子之前,你能预先知道骰子的点数是多少吗?
学生(齐答):不知道(有的学生小声地说这是随机的)。
教师:按照你小组的数据,点数1至6之间的各点数出现的频率是一样的吗?
学生3:我们小组各点数的频率都不一样,
学生4:我们小组投掷点数2和点数4的频率是一样的。
教师:为什么这两组同学的数据不相同呢?这说明了什么?
学生5:说明这件事情有可能发生也有可能不发生。
教师:分析得很好,在未掷骰子之前,你能确定一次掷出的点数不可能为8吗?你能确定一次掷出的点数必然是整数点吗?你能确定掷出的点数为4吗?
学生(齐答):能,能,不能。
点评:学生亲身参与活动,并利用活动得到的数据回答老师提出的问题,每一个学生都能积极地参与到课堂上来,把自己的结论与其他学生交流,增强了学习的自信心和合作探究的意识,在一问一答中逐渐理解“可能”、“不可能”、“必然”三个统计概念。
3学习点拨,分析概念
教师:通过上面的活动,你能对“可能”、“确定”、“不可能”、“必然”加以概括性描述吗?
(学生踊跃回答,互相补充,教师指正,以图表的形式在幻灯片上显示)
点评:由学生自己发现规律,通过语言加以概括性描述,增强学生数学语言表达能力,
4知识抢答
下列事件哪些是必然发生的?哪些是可能发生的?哪些是不可能发生的?
1两个有理数的和是零…………()
2天气预报说明天会下雨。…………()
3任意买一张电影票,座位号是偶数。()
4今天星期三,明天星期五。…………()
5从装有2个白球,3个红球的口袋中,摸出2个黄球。…………………………()
6打开电视,它正在播广告。…………()
点评:借助学生熟悉的事例,引起学生的兴趣,并通过抢答的形式增强学生竞争意识,加深学生对可能与确定的理解。
5情境编题,拓展升华
教师:前面大家做得非常出色,老师相信你们还会有更大的潜能!请各小组根据下列题意编写事件。
(1)将两个红球、一个黑球、一个白球放入袋中,搅匀后同时摸出两个,请根据此情境编写“不可能事件”、“可能事件”和“必然事件”各一个。
学生1:不可能事件:摸出两个黄球,可能事件:摸出一个黑球一个白球,必然事件:摸到的一定是两个球。
(部分同学因为最后一个问题偷偷地笑了起来)
教师:看来有些同学不赞成他的某些说法,还有补充吗?
学生2:我认为必然事件应该是摸出两球的颜色是红、白、黑三种颜色中的任意两种。
(全班学生点头表示赞同)
教师:这位同学抓住了这三个事件都是针对于球的颜色而言,观察得很仔细。
(2)每小组讨论后举出三个生活中的事件,分别是必然事件,随机事件,不可能事件,其他各组判定正误,并给出解释(注意:要贴近生活,符合实际生活)。
学生1:太阳从东边升起是必然事件;一本书共100页,一翻便翻到66页是随机事件;地球围绕月亮转是不可能事件,
教师:这位同学联系实际生活举例,很好。
学生2:苹果从苹果树上掉下来是必然事件,苹果从苹果树上掉下来砸到人的头上是随机事件,苹果从苹果树上飞到空中是不可能事件,
教师:这位同学把同一件事情分成三种不同的情况,很具有创新能力。
(学生2脸上露出喜悦的笑容,同学们向他投去敬佩的目光)
点评:本活动以小组为单位进行,各组独立思考,充分体现学生的主体地位,在活动中教师对活动能力较差的小组进行指导,在练习中强化学生对“可能”、“不可能”、“必然”的理解,同时又在开放性习题中发散学生的思维,增强学生数学语言表达能力,小组间相互评价,由浅入深,逐步将教学推向高潮。
6情境回顾
教师:现在大家能利用本节课所学的知识回答关于地震的问题了吗?
学生充满自信地回答:能。
点评:使学生通过本节课的学习,解决课前提出的实际问题,体会学习的快乐。
7师生小结归纳(略)
总评
1重视组织和开发课程资源
《数学课程标准》中指出:“从学生已有的生活经验出发,让学生亲身经历实际问题抽象成数学模型并进行解释与应用的过程。”本节课关注和利用学生经历过的事情(地震),以学生已有的生活经验和感受为出发点,让学生切实感受到生活中处处有数学。
2以问题为载体给学生提供探索空间
美国数学家哈尔莫斯指出:“问题是数学的心脏,学生有了问题才会探究,只有主动地去探究才会有创新、有创造,”本节课的每个环节的设计与展示,都以问题的解决为中心,探索规律先让学生做掷骰子活动,再以问题的形式带领学生探究,寻找规律,总结概念,在课堂练习中以抢答、情境编题等形式巩固知识、拓展升华,整节课构建了以“问题研究和学生活动”为中心的课堂学习环境。
3注重学生在学习过程中的自主体验
认知心理派代表人物布鲁纳曾说过:“知识的获得是一个主动的过程,学习者不应是信息的被动接受者,而应该是知识获取过程的主动参与者,”教学过程中,教师改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,关注学生的学习兴趣和经验,实施开放式教学,学生通过“掷骰子”活动得到的数据回答老师提出的问题,在这个过程中,很多后进生增强了自信心,获得了成功的喜悦,这也正是我们每个教育者所希望看到的。
“可能还是确定”属于初中概率与统计领域中的内容,是七年级数学继“数据的收集”与“数据的表示”之后的一个学习内容,它是从学生周围熟悉的问题入手,让学生置身于解决一些简单的实际问题的过程,体会数据的作用,感受大千世界的不确定性,进一步熟悉收集、整理、描述和分析数据的活动过程,理解频数、频率、不可能发生、可能发生和必然发生的概念,使用的教材是华师大版七年级下册第11章第一节“可能还是确定”。
教学过程
1创设情境,激发兴趣
情境投影:2008年5月12日四川省汶川县发生8.0级强烈地震,这次地震波及范围广,持续时间长,破坏性特别大,造成我国数百万同胞无家可归,给我们国家造成巨大的损失……
教师:通过这次地震,我想大家肯定对地震的发生和预防有了一个全新的认识,你能回答下面几个问题吗?
①在地震发生以前,我们是否能够确定地震发生的具体时间、地点和震级呢?
②地震的发生是一个必然事件、可能事件还是不可能事件呢?
③有人预测:重庆市近些年来没有发生过地震,以后也不会发生地震,也有人预测:前两天发生了余震,所以今天也一定会有余震,这些说法是否正确?为什么?
(话音刚落)学生顿时议论纷纷,
教师:(引入课题)同学们肯定对这件事很关注,也很想知道到底是怎样的,大家的猜测到底对不对呢?通过这节课的学习,大家就能够准确地回答以上的问题(板书:可能还是确定)!
(学生十分投入,热情很高)
点评:把学生感兴趣的、经历过的情境移植到数学课堂,易于激发学生的学习兴趣,使其产生跃跃欲试的探索意识,产生主动求知的心理冲动,为学生的自主学习和独立探索营造良好的氛围。
2探索新知
教师:下面我们来做一个掷骰子游戏,两位同学为一组,一位同学掷骰子20次,另一位同学记录,并完成表格,
(学生在分组实验时,教师走下讲台巡视、指导学生正确操作,鼓励学生相互协作、相互配合,共同完成活动)

教师:点数为7的频数是多少?频率是多少?
学生1:点数为7的频数是0,频率也是0。
教师(追问):若把掷骰子的次数改成100次,甚至更多,点数为7的频数及频率会不会发生变化?为什么?
学生1:不会变化,因为不可能掷出7这个点数,与掷骰子次数无关,
教师:很好,分析得很透彻,若在以上游戏中填表的点数一栏增加“点数小于7”和“点数不小于7”两栏,则不用实验我们就可以知道“点数小于7”的频数及频率,它们分别是多少?
学生2:点数小于7的频数是20,频率是100%。
教师(追问):为什么不需实验我们就可以知道?
学生2:因为掷出的点数都是小于7的(有的学生在下面小声地说发生的可能性是100%)。
教师:回答得很正确,在这个游戏中,掷得点数为3的频数各小组相同吗?
学生四周张望相邻小组的实验数据,都摇头表示不相同。
教师:在未掷骰子之前,你能预先知道骰子的点数是多少吗?
学生(齐答):不知道(有的学生小声地说这是随机的)。
教师:按照你小组的数据,点数1至6之间的各点数出现的频率是一样的吗?
学生3:我们小组各点数的频率都不一样,
学生4:我们小组投掷点数2和点数4的频率是一样的。
教师:为什么这两组同学的数据不相同呢?这说明了什么?
学生5:说明这件事情有可能发生也有可能不发生。
教师:分析得很好,在未掷骰子之前,你能确定一次掷出的点数不可能为8吗?你能确定一次掷出的点数必然是整数点吗?你能确定掷出的点数为4吗?
学生(齐答):能,能,不能。
点评:学生亲身参与活动,并利用活动得到的数据回答老师提出的问题,每一个学生都能积极地参与到课堂上来,把自己的结论与其他学生交流,增强了学习的自信心和合作探究的意识,在一问一答中逐渐理解“可能”、“不可能”、“必然”三个统计概念。
3学习点拨,分析概念
教师:通过上面的活动,你能对“可能”、“确定”、“不可能”、“必然”加以概括性描述吗?
(学生踊跃回答,互相补充,教师指正,以图表的形式在幻灯片上显示)
点评:由学生自己发现规律,通过语言加以概括性描述,增强学生数学语言表达能力,
4知识抢答
下列事件哪些是必然发生的?哪些是可能发生的?哪些是不可能发生的?
1两个有理数的和是零…………()
2天气预报说明天会下雨。…………()
3任意买一张电影票,座位号是偶数。()
4今天星期三,明天星期五。…………()
5从装有2个白球,3个红球的口袋中,摸出2个黄球。…………………………()
6打开电视,它正在播广告。…………()
点评:借助学生熟悉的事例,引起学生的兴趣,并通过抢答的形式增强学生竞争意识,加深学生对可能与确定的理解。
5情境编题,拓展升华
教师:前面大家做得非常出色,老师相信你们还会有更大的潜能!请各小组根据下列题意编写事件。
(1)将两个红球、一个黑球、一个白球放入袋中,搅匀后同时摸出两个,请根据此情境编写“不可能事件”、“可能事件”和“必然事件”各一个。
学生1:不可能事件:摸出两个黄球,可能事件:摸出一个黑球一个白球,必然事件:摸到的一定是两个球。
(部分同学因为最后一个问题偷偷地笑了起来)
教师:看来有些同学不赞成他的某些说法,还有补充吗?
学生2:我认为必然事件应该是摸出两球的颜色是红、白、黑三种颜色中的任意两种。
(全班学生点头表示赞同)
教师:这位同学抓住了这三个事件都是针对于球的颜色而言,观察得很仔细。
(2)每小组讨论后举出三个生活中的事件,分别是必然事件,随机事件,不可能事件,其他各组判定正误,并给出解释(注意:要贴近生活,符合实际生活)。
学生1:太阳从东边升起是必然事件;一本书共100页,一翻便翻到66页是随机事件;地球围绕月亮转是不可能事件,
教师:这位同学联系实际生活举例,很好。
学生2:苹果从苹果树上掉下来是必然事件,苹果从苹果树上掉下来砸到人的头上是随机事件,苹果从苹果树上飞到空中是不可能事件,
教师:这位同学把同一件事情分成三种不同的情况,很具有创新能力。
(学生2脸上露出喜悦的笑容,同学们向他投去敬佩的目光)
点评:本活动以小组为单位进行,各组独立思考,充分体现学生的主体地位,在活动中教师对活动能力较差的小组进行指导,在练习中强化学生对“可能”、“不可能”、“必然”的理解,同时又在开放性习题中发散学生的思维,增强学生数学语言表达能力,小组间相互评价,由浅入深,逐步将教学推向高潮。
6情境回顾
教师:现在大家能利用本节课所学的知识回答关于地震的问题了吗?
学生充满自信地回答:能。
点评:使学生通过本节课的学习,解决课前提出的实际问题,体会学习的快乐。
7师生小结归纳(略)
总评
1重视组织和开发课程资源
《数学课程标准》中指出:“从学生已有的生活经验出发,让学生亲身经历实际问题抽象成数学模型并进行解释与应用的过程。”本节课关注和利用学生经历过的事情(地震),以学生已有的生活经验和感受为出发点,让学生切实感受到生活中处处有数学。
2以问题为载体给学生提供探索空间
美国数学家哈尔莫斯指出:“问题是数学的心脏,学生有了问题才会探究,只有主动地去探究才会有创新、有创造,”本节课的每个环节的设计与展示,都以问题的解决为中心,探索规律先让学生做掷骰子活动,再以问题的形式带领学生探究,寻找规律,总结概念,在课堂练习中以抢答、情境编题等形式巩固知识、拓展升华,整节课构建了以“问题研究和学生活动”为中心的课堂学习环境。
3注重学生在学习过程中的自主体验
认知心理派代表人物布鲁纳曾说过:“知识的获得是一个主动的过程,学习者不应是信息的被动接受者,而应该是知识获取过程的主动参与者,”教学过程中,教师改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,关注学生的学习兴趣和经验,实施开放式教学,学生通过“掷骰子”活动得到的数据回答老师提出的问题,在这个过程中,很多后进生增强了自信心,获得了成功的喜悦,这也正是我们每个教育者所希望看到的。

