假设法在牛顿运动定律中的应用
翟元国

假设法是科学思维常用的手段之一,是一种推测性很强的思维方法,是分析与综合、归纳与演绎等复杂思维过程的前期思维活动,假设法极大地体现了逻辑推断的力量.在高中物理中,假设法被广泛运用,一般有假设条件、假设状态、假设过程等几种假设思路.
一、假设特殊条件得到一般性结论
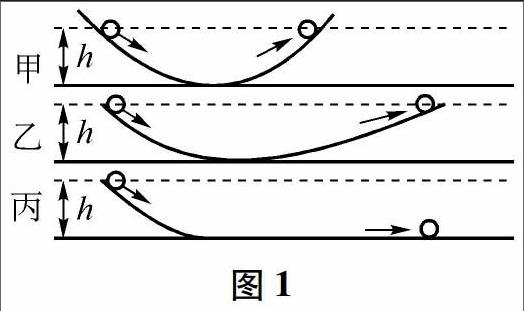
例1 十六世纪,伽利略和笛卡尔对物体的运动做了准确的描述,牛顿在伽利略和笛卡尔等人研究的基础上,结合自己的研究,系统地总结了力学知识,提出了牛顿运动三定律.伽利略用强有力的论据和逻辑力量推断出力是运动变化的原因,而不是维持运动的原因,我们来看下伽利略的理想实验,如图1所示,推断过程如下:
(1)(实验事实)两个对接的斜面,让静止的小球沿一个斜面滚下,小球将滚上另一个斜面.
(2)(科学假设)如果没有摩擦,小球将上升到释放时的高度.
(3)(合理外推)减小第二个斜面的倾角,如果没有摩擦小球在这个斜面上仍然要达到原来的高度.
(4)(合理外推)继续减小第二个斜面的倾角,最后使它咸水平,小球沿水平面做持续匀速直线运动.
(5)(合理推断)物体在水平面上做匀速运动时并不需要外力来维持.
伽利略理想实验的意义在于用“实验事实+科学假设+合理外推”的方法推翻了亚里士多德“力是维持物体运动的原因”的观点.伽利略理想实验的伟大之处在于巧妙利用假设法,将可靠实验基础之上的实验现象进行科学假设,以事实为依据,以抽象为指导,抓住主要因素,忽略次要因素,从而深刻地揭示了自然规律,打下机械运动学的第一根基桩,为牛顿的理论体系的建立奠定了基础.
二、假设临界状态得到极值范围
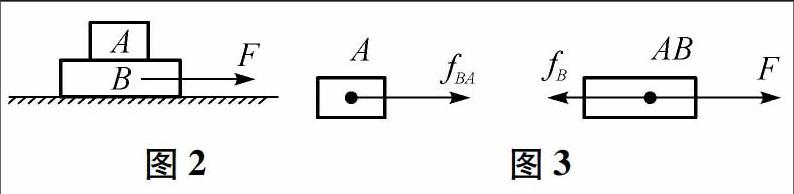
例2 如图2所示,水平地面上放置质量分别为m、2m的A、B两个物体,A、B间以及B与地面间的动摩擦系数均为μ,现用水平拉力F拉B,欲使A、B-起共同运动,则拉力F的大小范围为多少?
解析 本例的难点在于拉力F为何存在范围?何时最大?何时最小?解决难点的重点在于对两个物体的受力情况分析和对运动过程中物理量之间的逻辑关系的理解.如图3所示为A物体和两物体整体的水平方向受力(fB为地面对B的摩擦力),拉力F拉动物体B向右运动,因为A、B间的摩擦,A被B的摩擦力fBA带动也向右运动,并且B对4的摩擦力fBA=ma,随着拉力F的大小不同,A、B整体的加速度不同,B对A的摩擦力fBA也不同,加速度越大fBA也越大.
可以看出,如果题设求极值范围的条件不明显,可以分析题设物理量之间的内在逻辑关系,采用假设法假设出临界状态的物理量(如本例中的加速度最小值O和最大值μg),进而利用牛顿运动定律得到极值范围.
三、假设可能状态得到规律性结果
例3 如图4所示,小球B放在真空容器A内,球B的直径恰好等于A的正方形空腔的边长,将它们以初速度v。竖直向上抛出,试分析在不计空气阻力时A、B间的作用力情况.
解析 A对B的作用力可能向上,可能向下,也可能为零.如图5所示,分析B的受力,假设A对B的作用力向上,则B的加速度为G-N=ma,B的加速度方向向下且小于g.而对AB整体分析可知,AB整体只受到重力作用,加速度为g,B的加速度也应为g,A对B的作用力应该为零,结果与假设矛盾,假设错误.进而知道,只有当AB间的作用力为零时,B的加速度才与AB整体加速度相等.
例4 如图6所示,一皮带输送机的皮带以v=13.6m/s的速率做匀速运动,其有效输送距离AB=29.8m,与水平方向夹角为θ=37°.将一小物体轻放在A点,物体与皮带间的动摩擦因数μ=0.1,求物体由A运动到B所需的时间.(g=10m/s?)
此时,物体速度与皮带相等,但还没滑到底部,下一阶段物体如何运动呢?主要是摩擦力的方向向哪里?
假设此时没有摩擦力,可知物体具有沿斜面向下的加速度,物体要向下加速运动,皮带做的是匀速运动,则物体必然受到向上的摩擦力,且沿斜面向下的重力分力为,ngsin37°=0.6mg,沿斜面向上的滑动摩擦力大小为μmgcos37°=0.08mg,这两个力的合力向下,物
本例中,物体加速到速度与皮带相等后摩擦力的分析是问题的难点,解决难点的方法是假设此时没有摩擦力,从而看出物体相对于皮带的相对运动方向进而得到实际上摩擦力的方向使问题得到解决.
我们在使用假设法时,一般通过假设摩擦力或弹力等力的有或无,或假设某力的方向,或假设某过程如何进行等科学、合理的假设,充分揭示出牛顿运动定律问题中的多个物理量之间的逻辑关系,从而使隐蔽或复杂的物理量之间的关系趋于明朗化和简单化,找到直观、清晰的分析思路使问题得到解决.



假设法是科学思维常用的手段之一,是一种推测性很强的思维方法,是分析与综合、归纳与演绎等复杂思维过程的前期思维活动,假设法极大地体现了逻辑推断的力量.在高中物理中,假设法被广泛运用,一般有假设条件、假设状态、假设过程等几种假设思路.
一、假设特殊条件得到一般性结论
例1 十六世纪,伽利略和笛卡尔对物体的运动做了准确的描述,牛顿在伽利略和笛卡尔等人研究的基础上,结合自己的研究,系统地总结了力学知识,提出了牛顿运动三定律.伽利略用强有力的论据和逻辑力量推断出力是运动变化的原因,而不是维持运动的原因,我们来看下伽利略的理想实验,如图1所示,推断过程如下:
(1)(实验事实)两个对接的斜面,让静止的小球沿一个斜面滚下,小球将滚上另一个斜面.
(2)(科学假设)如果没有摩擦,小球将上升到释放时的高度.
(3)(合理外推)减小第二个斜面的倾角,如果没有摩擦小球在这个斜面上仍然要达到原来的高度.
(4)(合理外推)继续减小第二个斜面的倾角,最后使它咸水平,小球沿水平面做持续匀速直线运动.
(5)(合理推断)物体在水平面上做匀速运动时并不需要外力来维持.
伽利略理想实验的意义在于用“实验事实+科学假设+合理外推”的方法推翻了亚里士多德“力是维持物体运动的原因”的观点.伽利略理想实验的伟大之处在于巧妙利用假设法,将可靠实验基础之上的实验现象进行科学假设,以事实为依据,以抽象为指导,抓住主要因素,忽略次要因素,从而深刻地揭示了自然规律,打下机械运动学的第一根基桩,为牛顿的理论体系的建立奠定了基础.
二、假设临界状态得到极值范围
例2 如图2所示,水平地面上放置质量分别为m、2m的A、B两个物体,A、B间以及B与地面间的动摩擦系数均为μ,现用水平拉力F拉B,欲使A、B-起共同运动,则拉力F的大小范围为多少?
解析 本例的难点在于拉力F为何存在范围?何时最大?何时最小?解决难点的重点在于对两个物体的受力情况分析和对运动过程中物理量之间的逻辑关系的理解.如图3所示为A物体和两物体整体的水平方向受力(fB为地面对B的摩擦力),拉力F拉动物体B向右运动,因为A、B间的摩擦,A被B的摩擦力fBA带动也向右运动,并且B对4的摩擦力fBA=ma,随着拉力F的大小不同,A、B整体的加速度不同,B对A的摩擦力fBA也不同,加速度越大fBA也越大.
可以看出,如果题设求极值范围的条件不明显,可以分析题设物理量之间的内在逻辑关系,采用假设法假设出临界状态的物理量(如本例中的加速度最小值O和最大值μg),进而利用牛顿运动定律得到极值范围.
三、假设可能状态得到规律性结果
例3 如图4所示,小球B放在真空容器A内,球B的直径恰好等于A的正方形空腔的边长,将它们以初速度v。竖直向上抛出,试分析在不计空气阻力时A、B间的作用力情况.
解析 A对B的作用力可能向上,可能向下,也可能为零.如图5所示,分析B的受力,假设A对B的作用力向上,则B的加速度为G-N=ma,B的加速度方向向下且小于g.而对AB整体分析可知,AB整体只受到重力作用,加速度为g,B的加速度也应为g,A对B的作用力应该为零,结果与假设矛盾,假设错误.进而知道,只有当AB间的作用力为零时,B的加速度才与AB整体加速度相等.
例4 如图6所示,一皮带输送机的皮带以v=13.6m/s的速率做匀速运动,其有效输送距离AB=29.8m,与水平方向夹角为θ=37°.将一小物体轻放在A点,物体与皮带间的动摩擦因数μ=0.1,求物体由A运动到B所需的时间.(g=10m/s?)
此时,物体速度与皮带相等,但还没滑到底部,下一阶段物体如何运动呢?主要是摩擦力的方向向哪里?
假设此时没有摩擦力,可知物体具有沿斜面向下的加速度,物体要向下加速运动,皮带做的是匀速运动,则物体必然受到向上的摩擦力,且沿斜面向下的重力分力为,ngsin37°=0.6mg,沿斜面向上的滑动摩擦力大小为μmgcos37°=0.08mg,这两个力的合力向下,物
本例中,物体加速到速度与皮带相等后摩擦力的分析是问题的难点,解决难点的方法是假设此时没有摩擦力,从而看出物体相对于皮带的相对运动方向进而得到实际上摩擦力的方向使问题得到解决.
我们在使用假设法时,一般通过假设摩擦力或弹力等力的有或无,或假设某力的方向,或假设某过程如何进行等科学、合理的假设,充分揭示出牛顿运动定律问题中的多个物理量之间的逻辑关系,从而使隐蔽或复杂的物理量之间的关系趋于明朗化和简单化,找到直观、清晰的分析思路使问题得到解决.

