求合力的常用方法
张凌明

学习了重力、弹力、摩擦力等各种力之后,在对物体受力分析时发现物体的受力大多数情况下并不是单纯的受到一个力,所以就需要把物体受到的力进行组合,求出最终的合力,力的合成在高考中是必考内容之一.力的合成必须遵循“同物性”和“同时性”的原则.“同物性”是指待合成的诸力是作用在同一物体上的力,“同时性”是指待合成的诸力是同时出现的力.而求解合力的方法有多种,可以由平行四边形定则求合力、由矢量三角形定则求解合力、用图解法求解合力、正交分解法求解合力、用相似三角形求解合力.
一、平行四边形定则求解合力
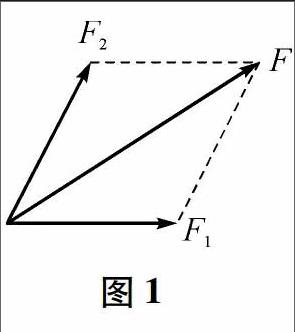
平行四边形定则:求两个互成角度的共点力F1、F2的合力,可以用表示Fl、F2的有向线段为邻边作平行四边形,平行四边形的对角线(在两个有向线段F1、F2之间)就表示合力的大小和方向,如图1所示.对于画出的平行四边形寻找(或者构造出)直角三角形,然后利用三角函数列出方程分析求解.
例1 在研究两个共点力F1、F2的合成实验中,得到如图2所示的合力F与两力夹角θ的关系图象.现有一物体在F1、F2、F3三个力的作用下保持静止状态,则F3可能为()
A.8N
B.12N
C.14N
D.16N
解析 本题考查平行四边形定则求合力、共点力的平衡.设F1>F2,由图象和平行四边形定则可知:当θ=π时,F=F1-F2=2N,当时,,两式联立解得F1=8N,F2=6N.则F1-F2≤F≤Fl+F2,即2N≤F≤14N.物体在F1、F2、F3三个力的作用下保持静止状态,由平衡条件可知,F3必与F等大反向,所以F3的取值范围为2N≤F3≤14N,故选项ABC正确.
例2 如图3所示,用两根等长轻绳将木板悬挂在竖直木桩上等高的两点,制成一简易秋千.某次维修时将两轻绳各剪去一小段,但仍保持等长且悬挂点不变.木板静止时,F1表示木板所受合力的大小,F2表示单根轻绳对木板拉力的大小,则维修后()
A.F1不变,F2变大
B.F1不变,F2变小
C.F1变大,F2变大
D.F1变小,F2变小
解析 本题考查受力分析、物体的平衡.在轻绳被剪短前后,木板都处于静止状态,所以木板所受的合力都为零,即F1=0.因两根轻绳等长,且悬挂点等高,故两根轻绳对木板的拉力相等,均为F2,对木板进行受力分析,如图4所示,把两根绳子的拉力作为平行四边形的邻边,画出平行四边形,则合力就与重力等值反向,则竖直方向平衡方程:2F2cosβ=G,轻绳剪去一段后,θ增大,cosθ减小,故F2变大.选项A正确.
二、矢量三角形法则求解合力
求两个互成角度的共点力F1、F2的合力,可以把表示F1、F2的线段首尾顺次相接地画出,把F1、F2的另外两端连接起来,则此连线就表示合力的大小和方向,如图5所示.如果物体在三个共点力的作用下处于平衡状态,则代表这三个力的有向线段构成封闭的矢量三角形,用矢量三角形法则解题,可避免繁琐的三角函数,使求解过程变得简单.
例2 如图6所示,用细绳将重球悬挂在光滑墙壁上,当绳子变长时()
A.绳子的拉力变小,墙对球的弹力变大
B.绳子的拉力变大,墙对球的弹力变大
C.绳子的拉力变大,墙对球的弹力变小
D.绳子的拉力变小,墙对球的弹力变小
解析 此题可以采用矢量三角形定则求解.选球为研究对象,球在重力G、细绳拉力T和墙壁弹力N三力作用下处于平衡状态,如图7所示.三力构成封闭的矢量三角形.当绳变长时α角变小,而G大小、方向都不变,N方向不变,故N、T都变小,即B选项正确.
三、图解法求解合力
图解法分析动态平衡问题的条件:往往涉及三个力,其中一个力为恒力,另一个力方向不变,但大小发生变化,第三个力则随外界条件的变化而变化,包括大小和方向都变化.先把除了恒力以外的两个力进行合成(合力与恒力等值反向),再根据平行四边形定则或者矢量三角形定则画出多组图象看出力的变化规律,解答此类“动态型”问题时,一定要认清哪些因素保持不变,哪些因素是改变的,这是解答动态问题的关键.
例4 如图8所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,将绳子BC逐渐缓慢地变化到沿水平方向,在这一过程中,绳子BC的拉力变化情况是()
A.增大
B.先减小,后增大
C.减小
D.先增大,后减小
解析 此题考查图解法求合力,对于结点受力分析,受到竖直向下的拉力FB(大小等于重力),两根倾斜绳子的拉力FAB、FCB,其中FB是恒力,FAB方向不变.FCB方向在发生改变.先把FAB和FCB进行合成,合力与恒力FB等值反向,然后采用图解法(画动态平行四边形或者矢量三角形).作出力的平行四边形,如图9所示.由图可看出,FCB先减小后增大.即B选项正确.
四、正交分解法求解合力
把物体所受的不同方向的各个力都分解到相互垂直的两个方向上去,然后再求每个方向上的分力的代数和,这样就把复杂的矢量运算转化成了简单的代数运算,最后再求两个互成90度角的合力就简便多了.正确选择直角坐标系,通常选择共点力的作用点为坐标原点,坐标轴x、y的选择可按下列原则去确定:a.尽可能使更多的力落在坐标轴上.b.沿物体运动方向或加速度方向建立一个坐标轴.如例4也可以采用正交分解法分析求解.
j析 如图10所示,将FAB、FCB分别沿水平方向和竖直方向分解,由两方向合力为零知:
显然,当θ=60度时,FCB最小,故当θ变大时,FCB先变小后变大.
五、相似三角形求解合力
正确作出力的三角形后,如能判定力的三角形与图形中已知长度的三角形(几何三角形)相似,则可用相似三角形对应边成比例求出三角形中力的比例关系,从而达到求未知量的目的。此种题型往往涉及三个力,其中一个力为恒力,另两个力的大小和方向均发生变化,则此时用相似三角形分析.相似三角形法是解平衡问题时常遇到的一种方法,解题的关键是正确的受力分析,寻找力三角形和几何三角形相似.
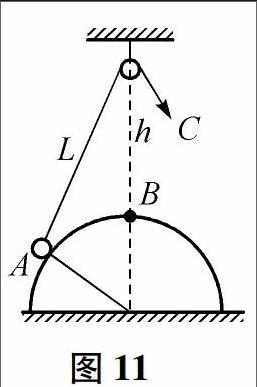
例5 如图11所示,半径为R的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B的距离为h,轻绳的一端系一小球,靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止,现缓慢地拉绳,在使小球由A到B的过程中,半球对小球的支持力Ⅳ和绳对小球的拉力T的大小变化的情况是()
A.N变大,T变小
B.N变小,T变大
C.N变小,T先变小后变大
D.N不变,T变小
解析 如图12所示,对小球:受力平衡,由于缓慢地拉绳,所以小球运动缓慢视为始终处于平衡状态,其中重力mg不变,支持力Ⅳ、绳子的拉力T一直在改变,但是总形成封闭的动态三角形(图中小阴影三角形).由于在这个三角形中有四个变量:支持力Ⅳ的大小和方向、绳子的拉力T的大小和方向,所以还要利用其它条件,实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式: 可得: 运动过程中L变小,T变小mg,运动中各量均为定值,支持力N不变,正确答案D.



学习了重力、弹力、摩擦力等各种力之后,在对物体受力分析时发现物体的受力大多数情况下并不是单纯的受到一个力,所以就需要把物体受到的力进行组合,求出最终的合力,力的合成在高考中是必考内容之一.力的合成必须遵循“同物性”和“同时性”的原则.“同物性”是指待合成的诸力是作用在同一物体上的力,“同时性”是指待合成的诸力是同时出现的力.而求解合力的方法有多种,可以由平行四边形定则求合力、由矢量三角形定则求解合力、用图解法求解合力、正交分解法求解合力、用相似三角形求解合力.
一、平行四边形定则求解合力
平行四边形定则:求两个互成角度的共点力F1、F2的合力,可以用表示Fl、F2的有向线段为邻边作平行四边形,平行四边形的对角线(在两个有向线段F1、F2之间)就表示合力的大小和方向,如图1所示.对于画出的平行四边形寻找(或者构造出)直角三角形,然后利用三角函数列出方程分析求解.
例1 在研究两个共点力F1、F2的合成实验中,得到如图2所示的合力F与两力夹角θ的关系图象.现有一物体在F1、F2、F3三个力的作用下保持静止状态,则F3可能为()
A.8N
B.12N
C.14N
D.16N
解析 本题考查平行四边形定则求合力、共点力的平衡.设F1>F2,由图象和平行四边形定则可知:当θ=π时,F=F1-F2=2N,当时,,两式联立解得F1=8N,F2=6N.则F1-F2≤F≤Fl+F2,即2N≤F≤14N.物体在F1、F2、F3三个力的作用下保持静止状态,由平衡条件可知,F3必与F等大反向,所以F3的取值范围为2N≤F3≤14N,故选项ABC正确.
例2 如图3所示,用两根等长轻绳将木板悬挂在竖直木桩上等高的两点,制成一简易秋千.某次维修时将两轻绳各剪去一小段,但仍保持等长且悬挂点不变.木板静止时,F1表示木板所受合力的大小,F2表示单根轻绳对木板拉力的大小,则维修后()
A.F1不变,F2变大
B.F1不变,F2变小
C.F1变大,F2变大
D.F1变小,F2变小
解析 本题考查受力分析、物体的平衡.在轻绳被剪短前后,木板都处于静止状态,所以木板所受的合力都为零,即F1=0.因两根轻绳等长,且悬挂点等高,故两根轻绳对木板的拉力相等,均为F2,对木板进行受力分析,如图4所示,把两根绳子的拉力作为平行四边形的邻边,画出平行四边形,则合力就与重力等值反向,则竖直方向平衡方程:2F2cosβ=G,轻绳剪去一段后,θ增大,cosθ减小,故F2变大.选项A正确.
二、矢量三角形法则求解合力
求两个互成角度的共点力F1、F2的合力,可以把表示F1、F2的线段首尾顺次相接地画出,把F1、F2的另外两端连接起来,则此连线就表示合力的大小和方向,如图5所示.如果物体在三个共点力的作用下处于平衡状态,则代表这三个力的有向线段构成封闭的矢量三角形,用矢量三角形法则解题,可避免繁琐的三角函数,使求解过程变得简单.
例2 如图6所示,用细绳将重球悬挂在光滑墙壁上,当绳子变长时()
A.绳子的拉力变小,墙对球的弹力变大
B.绳子的拉力变大,墙对球的弹力变大
C.绳子的拉力变大,墙对球的弹力变小
D.绳子的拉力变小,墙对球的弹力变小
解析 此题可以采用矢量三角形定则求解.选球为研究对象,球在重力G、细绳拉力T和墙壁弹力N三力作用下处于平衡状态,如图7所示.三力构成封闭的矢量三角形.当绳变长时α角变小,而G大小、方向都不变,N方向不变,故N、T都变小,即B选项正确.
三、图解法求解合力
图解法分析动态平衡问题的条件:往往涉及三个力,其中一个力为恒力,另一个力方向不变,但大小发生变化,第三个力则随外界条件的变化而变化,包括大小和方向都变化.先把除了恒力以外的两个力进行合成(合力与恒力等值反向),再根据平行四边形定则或者矢量三角形定则画出多组图象看出力的变化规律,解答此类“动态型”问题时,一定要认清哪些因素保持不变,哪些因素是改变的,这是解答动态问题的关键.
例4 如图8所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,将绳子BC逐渐缓慢地变化到沿水平方向,在这一过程中,绳子BC的拉力变化情况是()
A.增大
B.先减小,后增大
C.减小
D.先增大,后减小
解析 此题考查图解法求合力,对于结点受力分析,受到竖直向下的拉力FB(大小等于重力),两根倾斜绳子的拉力FAB、FCB,其中FB是恒力,FAB方向不变.FCB方向在发生改变.先把FAB和FCB进行合成,合力与恒力FB等值反向,然后采用图解法(画动态平行四边形或者矢量三角形).作出力的平行四边形,如图9所示.由图可看出,FCB先减小后增大.即B选项正确.
四、正交分解法求解合力
把物体所受的不同方向的各个力都分解到相互垂直的两个方向上去,然后再求每个方向上的分力的代数和,这样就把复杂的矢量运算转化成了简单的代数运算,最后再求两个互成90度角的合力就简便多了.正确选择直角坐标系,通常选择共点力的作用点为坐标原点,坐标轴x、y的选择可按下列原则去确定:a.尽可能使更多的力落在坐标轴上.b.沿物体运动方向或加速度方向建立一个坐标轴.如例4也可以采用正交分解法分析求解.
j析 如图10所示,将FAB、FCB分别沿水平方向和竖直方向分解,由两方向合力为零知:
显然,当θ=60度时,FCB最小,故当θ变大时,FCB先变小后变大.
五、相似三角形求解合力
正确作出力的三角形后,如能判定力的三角形与图形中已知长度的三角形(几何三角形)相似,则可用相似三角形对应边成比例求出三角形中力的比例关系,从而达到求未知量的目的。此种题型往往涉及三个力,其中一个力为恒力,另两个力的大小和方向均发生变化,则此时用相似三角形分析.相似三角形法是解平衡问题时常遇到的一种方法,解题的关键是正确的受力分析,寻找力三角形和几何三角形相似.
例5 如图11所示,半径为R的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B的距离为h,轻绳的一端系一小球,靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止,现缓慢地拉绳,在使小球由A到B的过程中,半球对小球的支持力Ⅳ和绳对小球的拉力T的大小变化的情况是()
A.N变大,T变小
B.N变小,T变大
C.N变小,T先变小后变大
D.N不变,T变小
解析 如图12所示,对小球:受力平衡,由于缓慢地拉绳,所以小球运动缓慢视为始终处于平衡状态,其中重力mg不变,支持力Ⅳ、绳子的拉力T一直在改变,但是总形成封闭的动态三角形(图中小阴影三角形).由于在这个三角形中有四个变量:支持力Ⅳ的大小和方向、绳子的拉力T的大小和方向,所以还要利用其它条件,实物(小球、绳、球面的球心)形成的三角形也是一个动态的封闭三角形(图中大阴影三角形),并且始终与三力形成的封闭三角形相似,则有如下比例式: 可得: 运动过程中L变小,T变小mg,运动中各量均为定值,支持力N不变,正确答案D.

