浅析转化与化归思想在高三数列专题复习中的应用
范建珍
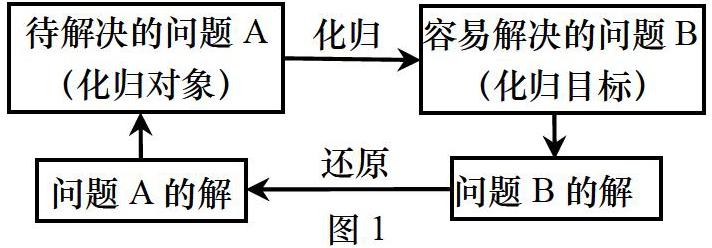


化归与转化思想是重要的数学思想方法之一,它是学生运用所学知识解决数学问题的重要途径,是处理解决复杂问题方法的精髓,是知识转化为能力的桥梁,是培养核心素养的沃土[1].所谓的化归与转化思想是指在研究或解决数学问题时,借助观察、联想、分析、类比等思维方式,将问题变换归结为已经解决或者比较容易解决的问题,进而使原问题得到解决的一种解题策略[2].简而言之,即“化生为熟、化繁为筒、化难为易、化未知为已知”,转化和化归的特点是通过不断转化实现问题的熟悉化、简单化、直观化、特殊化等,以便应用已知的知识和方法达到问题的有效解决[1],其一般模式如图1:
在数学学习的过程中处处都体现着转化与化归思想,常见的转化有一般与特殊的转化、正与反的转化,特殊与一般的转化,整体与局部的转化,高维与低维的转化,数与形的转化、等价转化等,
数列是高中数学的重要内容,是高考考查的重点,纵观近年来新课标全国卷对数列考查的重点是以等差等比数列为载体,包括常见的简单变形,考查学生对数列基础知识和基本技能的掌握,以及运用所学知识经验解决问题的能力和素养,特别是对“推理论证能力”、“运算求解能力”、“应用意识”以及“逻辑推理”和“数学运算”的考查.
由于数列公式多、计算杂、题型多样,且常与其他知识点结合起来考察,所以对于基础薄弱的高中校学生来说难度较大,学生常常因记忆不全,“思想”不明,用法不清,逻辑混乱,思维受限制,再加上运算能力低下,以及缺少反思感悟,因此在數列问题上出错概率较大,失分现象较为普遍,本文以数列问题为例从四个方面阐述化归与转化思想在高三专题复习的应用,以例题为载体,以化归与转化思想渗透为核心,通过对基础知识的梳理构建和基本题型的变式训练,以期达到串“点”成“线”的目的,促进学生对基础知识的掌握、基本技能的形成以及相应能力素养的发展,切实提高复习的有效性.
1 陌生问题熟悉化
在教学实际中,常常会看到这样的现象:基本公式学生是会的,但是有些学生却不明白什么时候该用哪个公式,因此在教学中应教学生学会将陌生问题熟悉化,并运用已有的知识、经验和方法解决当前问题,
设计意图首先,例1和变式1既先让学生尝到到陌生问题熟悉化的“甜头”,又起到温“等差、等比数列定义公式”之故,进而为知“更为陌生的问题熟悉化”之新做铺垫,让学生把数列问题转化为简单的等差、等比数列问题,再借助等差、等比数列的定义和通项公式解决问题,让学生养成不断回到概念去,是解决数列问题的常见的转化思路;其次,随着变式2~4问题的难度的逐步加大和问题形式的不断复杂化,让学生通过启发和引导不断地“化陌生为熟悉”,逐步掌握“陌生问题熟悉化”的基本“程序”,这样设计符合学生的认知规律,激发学生探索的热情,让学生全面看待问题,学会合理转化,感悟化归与转化的思想方法,把握等差等比数列定义的本质,熟练基本公式,通过启发引导使学生不断实现“从陌生到熟悉、从不懂到懂”,掌握基础知识,形成基本技能,积累基本活动经验.
2 未知问题已知化
当解决问题方向模糊时,可以通过适当对问题的表面形式加以挖掘、探究,找到“沟通”已知的“连结点”,进而达到未知问题已知化的目的,再借助已有的知识、经验和方法解决问题,
变式5若把例1条件“在x-y+1=0上”改为条件“在x-y+2n+l=0上”,其它条件不变,求数列{an}的通项公式,
变式6 若把例1条件“在x-y+l=0上”改为条件“在x-y+3”=0上”,其它条件不变,求数列{an}的通项公式,
变式7 若把例1条件“在x-y+1=0上”改为条件“在上”,其它条件不变,求数列{an}的通项公式,
变式8若把例1条件“在x-y+1=0上”改为条件“在4x-y+1=0上”,其它条件不变,求数列{an}的通项公式,
变式9 若把例1条件“在x-y+1=0上”改为条件“在4x-y+3”=0上”,其它条件不变,求数列{an}的通项公式,
变式10 若把例1条件“点Pn(an,an+1)(n∈N*)改为“只(Sn,an+1)(n∈N*)”,其它条件不变,求数列{an}的通项公式,
变式11 若把例1条件“点Pn(an,an+1)(n∈N*)在x-y+l=0上”改为“P(Sn,Sn+1,an+1)(n∈N*)在x-y=O上”,其它条件不变,求数列{an}的通项公式,
设计意图 首先通过变式5~7的解决让学生进一步对等差、等比数列的定义进行辨析,把握等差、等比数列定义的本质,同时回顾等差等比数列通项公式的求法,让学生学会将知识、方法进行正向迁移,从而达到未知问题已知化的目的;其次通过变式8,9的解决,让学生逐步学会“透过现象看本质”,并将未知问题已知化,让学生体验感悟将新问题化为老问题,即努力将新问题化归为等差、等比数列基本问题来解决是解决数列问题的基本思路和常规做法,合理转化,渗透定义法、加K法、倒数法、叠加法、累乘法等;再次抛出变式10,11让学生探究,加强比较,让学生感悟在a与Sn同时出现的关系式中,一般通过进行转化,使关系式仅含an或Sn,再根据情况进行处理,学生动脑独立思考尝试解答,并参与编题,加深学生对此类题型的印象;通过长期这样的基本技能演练和数学思想方法的熏陶,学生就能逐步地将教师的做法转化为其自觉行为,从而能逐步较有“章法”地解决数列问题.
3 复杂问题简单化
通过一定形式的变形转换将复杂问题化归为熟悉的简单问题,通过对简单问题的解答,达到解决复杂问题的目的,或者获得某种解决问题的启示[1].
例2 (1)已知数列{an}满足an+1=2an+3x2n,a1=2,求数列{an)的通项公式,本例(3)尝试让学生体验把数列问题转化为函数问题,引导学生执行数学运算三步曲:理解、选择、运算,注重方法的选择,规范答题的板书,结合课件展示,最值问题是普通高中学生掌握较为薄弱的题型,学生往往不知道如何下手,从何入题,结合学生实际,我们在平时的教学中,应该逐步渗透并总结出求数列最值问题的方法:(1)转化为函数的单调性;(2)运用递推公式,通过例2的解决让学生体验通过一定形式的变形转换,将复杂的问题化归为我们所熟悉的简单问题,使问题得以轻松解决,让学生亲历如何由“山重水复”到“柳暗花明”的过程,掌握通解同法、形成基本技能、感悟思想方法、积累基本活动经验.
4 抽象问题具体化
通过考察问题的极端元素,灵活地借助特殊问题解题,避开抽象及复杂运算,优化解题过程,降低解题难度[1],
设计意图本例(1)用基本量法可以解决,但本题是填空题,在考试时最好能做到“省时、准确”,由题意可知,只要满足a1,a3,a9成等比数列的条件,数列{an}取何种等差数列与所求代数式的值无关,因此可以将抽象数列具体化,例如a=n,则课轻松求得本例(2)的解决具体化方法则更显优势,结合题目信息,通过考察问题的特殊元素(即特值法),灵活地借助特殊问题解题,避开抽象及复杂运算,优化解题过程,降低解题难度.
5 结束语
数学思想方法是数学的精髓和灵魂,因此数学教学中数学教师应树立“思想”意识,将隐性的思想方法充分的地挖掘出来使之显性化,并贯穿在课堂教学的全过程,然而罗马不是一天就盖起来的,数学思想方法的渗透、掌握和灵活运用需要长期不懈的努力,但只要用心浇灌定能结出硕果,
参考文献
[1]詹爽姿.数学高考中的化归与转化思想[J].中学教研(数学),2016(3): 41-45
[2]杨恩彬,柯跃海,陈清华.化归与转化思想的数学能力统领功能探析[J].福建中学数学, 2013 (10):4-7



化归与转化思想是重要的数学思想方法之一,它是学生运用所学知识解决数学问题的重要途径,是处理解决复杂问题方法的精髓,是知识转化为能力的桥梁,是培养核心素养的沃土[1].所谓的化归与转化思想是指在研究或解决数学问题时,借助观察、联想、分析、类比等思维方式,将问题变换归结为已经解决或者比较容易解决的问题,进而使原问题得到解决的一种解题策略[2].简而言之,即“化生为熟、化繁为筒、化难为易、化未知为已知”,转化和化归的特点是通过不断转化实现问题的熟悉化、简单化、直观化、特殊化等,以便应用已知的知识和方法达到问题的有效解决[1],其一般模式如图1:
在数学学习的过程中处处都体现着转化与化归思想,常见的转化有一般与特殊的转化、正与反的转化,特殊与一般的转化,整体与局部的转化,高维与低维的转化,数与形的转化、等价转化等,
数列是高中数学的重要内容,是高考考查的重点,纵观近年来新课标全国卷对数列考查的重点是以等差等比数列为载体,包括常见的简单变形,考查学生对数列基础知识和基本技能的掌握,以及运用所学知识经验解决问题的能力和素养,特别是对“推理论证能力”、“运算求解能力”、“应用意识”以及“逻辑推理”和“数学运算”的考查.
由于数列公式多、计算杂、题型多样,且常与其他知识点结合起来考察,所以对于基础薄弱的高中校学生来说难度较大,学生常常因记忆不全,“思想”不明,用法不清,逻辑混乱,思维受限制,再加上运算能力低下,以及缺少反思感悟,因此在數列问题上出错概率较大,失分现象较为普遍,本文以数列问题为例从四个方面阐述化归与转化思想在高三专题复习的应用,以例题为载体,以化归与转化思想渗透为核心,通过对基础知识的梳理构建和基本题型的变式训练,以期达到串“点”成“线”的目的,促进学生对基础知识的掌握、基本技能的形成以及相应能力素养的发展,切实提高复习的有效性.
1 陌生问题熟悉化
在教学实际中,常常会看到这样的现象:基本公式学生是会的,但是有些学生却不明白什么时候该用哪个公式,因此在教学中应教学生学会将陌生问题熟悉化,并运用已有的知识、经验和方法解决当前问题,
设计意图首先,例1和变式1既先让学生尝到到陌生问题熟悉化的“甜头”,又起到温“等差、等比数列定义公式”之故,进而为知“更为陌生的问题熟悉化”之新做铺垫,让学生把数列问题转化为简单的等差、等比数列问题,再借助等差、等比数列的定义和通项公式解决问题,让学生养成不断回到概念去,是解决数列问题的常见的转化思路;其次,随着变式2~4问题的难度的逐步加大和问题形式的不断复杂化,让学生通过启发和引导不断地“化陌生为熟悉”,逐步掌握“陌生问题熟悉化”的基本“程序”,这样设计符合学生的认知规律,激发学生探索的热情,让学生全面看待问题,学会合理转化,感悟化归与转化的思想方法,把握等差等比数列定义的本质,熟练基本公式,通过启发引导使学生不断实现“从陌生到熟悉、从不懂到懂”,掌握基础知识,形成基本技能,积累基本活动经验.
2 未知问题已知化
当解决问题方向模糊时,可以通过适当对问题的表面形式加以挖掘、探究,找到“沟通”已知的“连结点”,进而达到未知问题已知化的目的,再借助已有的知识、经验和方法解决问题,
变式5若把例1条件“在x-y+1=0上”改为条件“在x-y+2n+l=0上”,其它条件不变,求数列{an}的通项公式,
变式6 若把例1条件“在x-y+l=0上”改为条件“在x-y+3”=0上”,其它条件不变,求数列{an}的通项公式,
变式7 若把例1条件“在x-y+1=0上”改为条件“在上”,其它条件不变,求数列{an}的通项公式,
变式8若把例1条件“在x-y+1=0上”改为条件“在4x-y+1=0上”,其它条件不变,求数列{an}的通项公式,
变式9 若把例1条件“在x-y+1=0上”改为条件“在4x-y+3”=0上”,其它条件不变,求数列{an}的通项公式,
变式10 若把例1条件“点Pn(an,an+1)(n∈N*)改为“只(Sn,an+1)(n∈N*)”,其它条件不变,求数列{an}的通项公式,
变式11 若把例1条件“点Pn(an,an+1)(n∈N*)在x-y+l=0上”改为“P(Sn,Sn+1,an+1)(n∈N*)在x-y=O上”,其它条件不变,求数列{an}的通项公式,
设计意图 首先通过变式5~7的解决让学生进一步对等差、等比数列的定义进行辨析,把握等差、等比数列定义的本质,同时回顾等差等比数列通项公式的求法,让学生学会将知识、方法进行正向迁移,从而达到未知问题已知化的目的;其次通过变式8,9的解决,让学生逐步学会“透过现象看本质”,并将未知问题已知化,让学生体验感悟将新问题化为老问题,即努力将新问题化归为等差、等比数列基本问题来解决是解决数列问题的基本思路和常规做法,合理转化,渗透定义法、加K法、倒数法、叠加法、累乘法等;再次抛出变式10,11让学生探究,加强比较,让学生感悟在a与Sn同时出现的关系式中,一般通过进行转化,使关系式仅含an或Sn,再根据情况进行处理,学生动脑独立思考尝试解答,并参与编题,加深学生对此类题型的印象;通过长期这样的基本技能演练和数学思想方法的熏陶,学生就能逐步地将教师的做法转化为其自觉行为,从而能逐步较有“章法”地解决数列问题.
3 复杂问题简单化
通过一定形式的变形转换将复杂问题化归为熟悉的简单问题,通过对简单问题的解答,达到解决复杂问题的目的,或者获得某种解决问题的启示[1].
例2 (1)已知数列{an}满足an+1=2an+3x2n,a1=2,求数列{an)的通项公式,本例(3)尝试让学生体验把数列问题转化为函数问题,引导学生执行数学运算三步曲:理解、选择、运算,注重方法的选择,规范答题的板书,结合课件展示,最值问题是普通高中学生掌握较为薄弱的题型,学生往往不知道如何下手,从何入题,结合学生实际,我们在平时的教学中,应该逐步渗透并总结出求数列最值问题的方法:(1)转化为函数的单调性;(2)运用递推公式,通过例2的解决让学生体验通过一定形式的变形转换,将复杂的问题化归为我们所熟悉的简单问题,使问题得以轻松解决,让学生亲历如何由“山重水复”到“柳暗花明”的过程,掌握通解同法、形成基本技能、感悟思想方法、积累基本活动经验.
4 抽象问题具体化
通过考察问题的极端元素,灵活地借助特殊问题解题,避开抽象及复杂运算,优化解题过程,降低解题难度[1],
设计意图本例(1)用基本量法可以解决,但本题是填空题,在考试时最好能做到“省时、准确”,由题意可知,只要满足a1,a3,a9成等比数列的条件,数列{an}取何种等差数列与所求代数式的值无关,因此可以将抽象数列具体化,例如a=n,则课轻松求得本例(2)的解决具体化方法则更显优势,结合题目信息,通过考察问题的特殊元素(即特值法),灵活地借助特殊问题解题,避开抽象及复杂运算,优化解题过程,降低解题难度.
5 结束语
数学思想方法是数学的精髓和灵魂,因此数学教学中数学教师应树立“思想”意识,将隐性的思想方法充分的地挖掘出来使之显性化,并贯穿在课堂教学的全过程,然而罗马不是一天就盖起来的,数学思想方法的渗透、掌握和灵活运用需要长期不懈的努力,但只要用心浇灌定能结出硕果,
参考文献
[1]詹爽姿.数学高考中的化归与转化思想[J].中学教研(数学),2016(3): 41-45
[2]杨恩彬,柯跃海,陈清华.化归与转化思想的数学能力统领功能探析[J].福建中学数学, 2013 (10):4-7

