基于MPCK视角下的二次函数复习设计与反思
蒋冲
[摘? 要] 文章从MPCK视角,以二次函数复习为例,通过设计与反思,以提高复习课教学的有效性.
[关键词] 初中数学;二次函数;MPCK;复习课
九年级的第一轮复习要求对学过的数学知识进行再理解、再学习,使学生构建科学的知识框架,对其中涉及的数学思想方法再次提高认识. 在MPCK理论的指导下,作为九年级教师,在复习课设计时要做如下构思:课标中对此部分内容是如何要求的?如何培养学生的思维能力?如何让学生深刻把握其中的数学思想方法?在过去几年里中考对此部分知识是如何考查的?学生对这部分知识的掌握程度如何?学生通过复习后应达到什么要求?当教师对这些问题进行考虑之后,就能做到有的放矢,对症下药.
MPCK视角下二次函数的复习
设计
MPCK视角下的中考复习设计,教师要认识复习内容在数学知识体系的地位,知道这部分知识在中考里呈现的方式及应达到的要求,以及学生近阶段的学习状况如何. 需要强调的是,学生复习并不是知识的简单重现,而是通过复习对旧知有新的认识,了解知识间的联系,提高学生的应用意识与实践能力.
1. 课标对“二次函数”的要求
《义务教育数学课程标准(2011年版)》对二次函数部分作如下描述:通过对实际问题的分析,体会二次函数的意义;会用描点法画出二次函数的图像,通过图像了解二次函数的性质;会用配方法将数字系数的二次函数的表达式化为y=a(x-h)2+k的形式,并能由此得到二次函数图像的顶点坐标,说出图像的开口方向,画出图像的对称轴,并能解决简单实际问题;会利用二次函数的图像求一元二次方程的近似解;知道给定不共线三点的坐标可以确定一个二次函数.
2. 近五年江苏中考对二次函数考查的统计(表1)
我们看到,最近五年江苏中考对二次函数的考查形式为填空题和解答题,其中填空题重点考查二次函数的图像与性质,解答题重点考查二次函数表达式的确定,二次函数与几何图形的综合.
3. 二次函数基础知识回顾
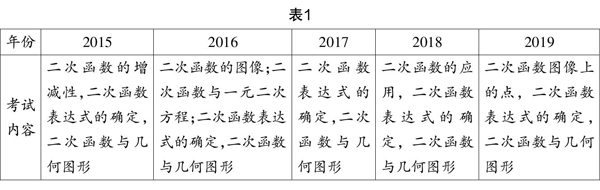
问题1:如图1所示,观察二次函数的图像,请说出尽可能多的结论.
问题2:能否求出此二次函数的解析式?若不能求出,适当添加条件,求出一个符合题意的解析式.
问题3:根据函数图像,请自编一个问题来解答.
设计意图? 这些问题都是结论开放性问题,通过解决问题,复习了二次函数的概念和图像,二次函数的性质及解析式的确定,学生因为需要观察图像才能解答问题,所以渗透了数形结合的数学思想,让学生多角度思考同一问题,体现了不同知识间的联系,开启了学生的思维.
4. 二次函数的应用
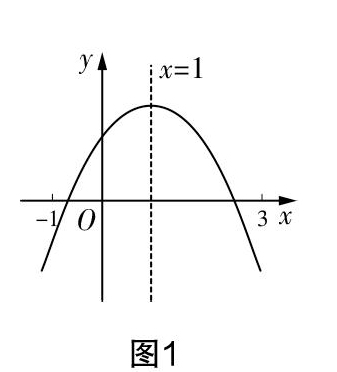
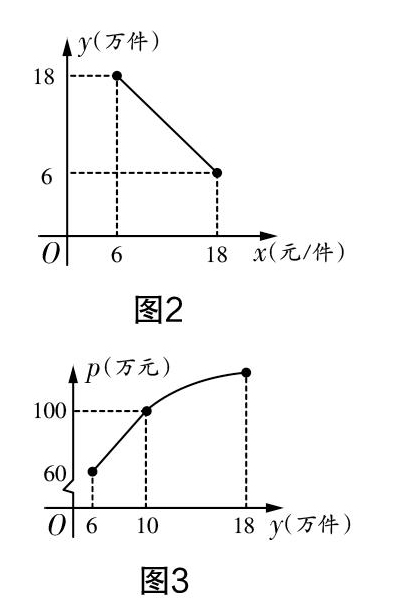
问题4:某公司抓住“一带一路”的机遇不断创新发展,生产销售某产品,该产品销售量y(万件)与售价x(元/件)之间存在图2(一条线段)所示的变化趋势,总成本P(万元)与销售量y(万件)之间存在图3所示的变化趋势,当6≤y≤10时可看成一条线段,当10≤y≤18时可看成抛物线P=-■y2+8y+m.
(1)写出y与x之间的函数关系式;
(2)若销售量不超过10万件时,利润为45万元,求此时的售价为多少元/件?
(3)当售价为多少元时,利润最大,最大值是多少万元?(利润=销售总额一总成本)
设计意图? 通过几个递进式的问题,(1)让学生结合实际问题,明白常量、变量代表的实际意义,能够解读特殊点的实际意义;(2)让学生学会从函数的角度看待问题,将实际问题转化为函数问题加以解决;(3)让学生体验求函数表达式的两种方法:一是待定系数法,二是实际意义法;(4)让学生了解不同变量之间的函数关系,如:销量与售价成一次函数关系,成本与销量之间成分段函数关系,销售利润与售价成二次函数关系等,增加学生综合运用多种数学知识解决实际问题的能力;(5)学生需要通过函数图像解决函数问题,又一次体验到数形结合的数学思想,并感受函数的本质——变化与趋势.
5. 二次函数的反馈训练
问题5:如图4,认真观察图像,请根据图像编写一个故事情节,在这个情境要求只出现两个变量x,y,这两个变量适合图示的函数关系,说明x,y的实际含义,使用图像中出现的有关数据说明变化过程的实际含义,及特殊点的含义.
6. 课堂归纳
本节课我们复习了二次函数的图像、性质及应用,你有什么收获吗?你对二次函数有什么新的认识?
设计意图? 当堂总結,跟踪练习,把已学习的二次函数知识和方法,归入学生自己的知识体系中,让这些知识与方法成为以后可反复利用的学习方法.
反思MPCK视角下的中考复习
从MK的角度来看,九年级数学教师应对初中数学知识了如指掌,明白各部分知识之间的联系,对每一部分知识蕴含的数学思想方法都清楚明白,在九年级一轮复习中,能够挑选出一些既考基础知识,也具有探究性的典型例题. 教师在复习二次函数前,要对课程标准与中考说明及检测都有所了解,了解二次函数在整个函数及初中数学中的地位与作用.
从PK的角度来看,整堂设计以一条抛物线贯穿始终,先让学生从二次函数图像与性质的回顾开始,再到解析式的确定,最后是二次函数的应用,通过开放性问题,触发学生的思维,通过与实际问题相结合,增强学生的应用意识与实践能力.
从CK的角度来看,教师在复习之前,对学生掌握知识的状况要做深入了解,关注近阶段学生的心理状况,估计在复习过程可能遇到的知识障碍与思维障碍. 教师要选择适当的问题情境和呈现方式进行课堂设计,从不同的侧面让学生掌握二次函数,充分考虑学生的个性差异,从学生的角度看待与设计问题,培养学生综合运用知识的能力.

